Hyperbolische Spirale
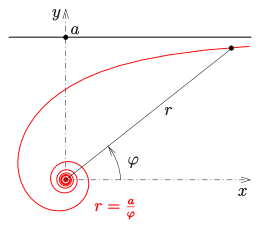
Eine hyperbolische Spirale ist eine ebene Kurve, die sich in Polardarstellung durch die Gleichung
einer Hyperbel beschreiben lässt. Da sie sich auch als Inversion (Kreisspiegelung) einer archimedischen Spirale auffassen lässt, heißt die Kurve auch reziproke Spirale.
1704 studierte Pierre Varignon diese Kurve. Auch Johann Bernoulli und Roger Cotes beschäftigten sich später damit.[1]
Beschreibung in kartesischen Koordinaten
[Bearbeiten | Quelltext bearbeiten]Die hyperbolische Spirale mit der Polargleichung
lässt sich in kartesischen Koordinaten durch die Parameterdarstellung
beschreiben.
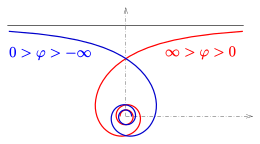
Die Hyperbel in der --Ebene besitzt die Koordinatenachsen als Asymptoten. Die hyperbolische Spirale (in der --Ebene) nähert sich für dem Nullpunkt an. Für ergibt sich eine Asymptote (s. nächsten Abschnitt).
Aus der Parameterdarstellung und ergibt sich eine Darstellung mit einer Gleichung:
Eigenschaften
[Bearbeiten | Quelltext bearbeiten]Asymptote
[Bearbeiten | Quelltext bearbeiten]Wegen
hat die Kurve eine
- Asymptote mit der Gleichung
Krümmung
[Bearbeiten | Quelltext bearbeiten]Mit der Formel
für die Krümmung einer Kurve in Polardarstellung und den Ableitungen und der hyperbolischen Spirale ergibt sich für die Krümmung
Inversion einer archimedischen Spirale
[Bearbeiten | Quelltext bearbeiten]
Die Spiegelung am Einheitskreis (Inversion) lässt sich in Polarkoordinaten durch beschreiben.
- Das Bild der archimedischen Spirale mit ist bei der Spiegelung am Einheitskreis die hyperbolische Spirale mit der Gleichung
Für schneiden sich beide Kurven in einem Fixpunkt auf dem Einheitskreis.
Der Krümmungskreis der archimedischen Spirale im Nullpunkt hat den Radius (siehe Krümmung der archimedischen Spirale) und den Mittelpunkt . Dieser Kreis geht bei der Kreisspiegelung in die Gerade über (siehe Inversion). Also gilt:
- Das Urbild der Asymptote der hyperbolischen Spirale bei der Kreisspiegelung der archimedischen Spirale ist der Krümmungskreis der archimedischen Spirale im Nullpunkt.
- Beispiel
Das Bild zeigt ein Beispiel mit . Der Kurvenbogen der archimedischen Spirale (grün), der im Einheitskreis (rot) liegt, wird auf den Teil der hyperbolischen Spirale (blau) abgebildet, der außerhalb des Kreises liegt.
Bogenlänge
[Bearbeiten | Quelltext bearbeiten]Die Länge des Bogens einer hyperbolischen Spirale zwischen zwei Punkten lässt sich mit der Formel für Kurven in Polardarstellung berechnen:

Sektorfläche
[Bearbeiten | Quelltext bearbeiten]Den Flächeninhalt eines Sektors der hyperbolischen Spirale berechnet man in Polarkoordinaten:
Zentralprojektion einer Schraublinie
[Bearbeiten | Quelltext bearbeiten]Die Zentralprojektion einer Schraublinie ist eine hyperbolische Spirale, falls Hauptpunkt und Augpunkt auf der Schraubachse liegen, siehe Schraublinie (Darstellende Geometrie).
Literatur
[Bearbeiten | Quelltext bearbeiten]- I. N. Bronstein, K. A. Semendjajew: Taschenbuch der Mathematik, Harri Deutsch Verlag, 1983, ISBN 3871444928, S. 146.
- Hans-Jochen Bartsch, Michael Sachs: Taschenbuch mathematischer Formeln für Ingenieure und Naturwissenschaftler, Carl Hanser Verlag, 2018, ISBN 3446457070, 9783446457072, S. 410.
- Kinko Tsuji, Stefan C. Müller: Spirals and Vortices: In Culture, Nature, and Science, Springer, 2019, ISBN 3030057984, 9783030057985, S. 96.
- Pierre Varignon: Nouvelle formation de Spirales – exemple II, Mémoires de l’Académie des sciences de l’Institut de France, 1704, S. 94–103.
- Friedrich Grelle: Analytische Geometrie der Ebene, Verlag F. Brecke, 1861 hyperbolische Spirale, S. 215.
- Jakob Philipp Kulik: Lehrbuch der höhern Analysis, Band 2, In Commiss. bei Kronberger u. Rziwnatz, 1844, Spirallinien, S. 222.
Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ John J. O’Connor, Edmund F. Robertson: Hyperbolic Spiral. In: MacTutor History of Mathematics archive (englisch).






























![{\displaystyle \qquad =a{\Big [}-{\frac {\sqrt {1+\varphi ^{2}}}{\varphi }}+\ln(\varphi +{\sqrt {1+\varphi ^{2}}}){\Big ]}_{\varphi _{1}}^{\varphi _{2}}\ .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec419a4f71975272ff387580423806e97ffe3e19)

