Tetraedergruppe

Ein reguläres Tetraeder, ein Beispiel eines Körpers mit voller Tetraeder-Symmetrie

Die Tetraedergruppe ist die Gruppe aller Symmetrieelemente (Punktgruppe) des regelmäßigen und homogenen Tetraeders (Dreieckspyramide, Vierflach). Sie ist isomorph zur symmetrischen Gruppe ${\displaystyle S_{4}}$. Das regelmäßige Tetraeder gehört zu den fünf Platonischen Körpern, den Körpern mit größtmöglicher Symmetrie. Es ist der einfachste dieser Körper und der einzige von ihnen, der nicht punktsymmetrisch ist. Das Tetraeder ist zu sich selbst dual und nimmt deshalb unter den fünf regulären Körpern eine Sonderstellung ein.

Ein (beliebiges) Tetraeder hat unter allen Polyedern die geringste Anzahl an Flächen, Ecken und Kanten. Es wird, weil einfach, auch Simplex des dreidimensionalen Raums genannt. Mit Tetraedern allein kann der (dreidimensionale) Raum nicht gefüllt werden („3D-Parkettierung“). In Kristallen tritt es im kubischen Kristallsystem auf.

Die Tetraedergruppe ist eine der 12 Gruppentypen mit 24 Symmetrieelementen, die keine abelschen Gruppen sind. In der Molekülphysik und Kristallographie kennzeichnet man die volle Gruppe des Tetraeders gemäß der Schoenflies-Symbolik der Punktgruppen und Raumgruppen mit dem Symbol ${\displaystyle T_{d}}$ und die Tetraeder-Drehgruppe mit dem Symbol ${\displaystyle T}$.^[1]

Wie bei anderen geometrischen Körpern auch kann man den Symmetrietyp mit Symbolen der Schoenflies-Symbolik der Symmetrieelemente wie folgt unterscheiden: ${\displaystyle C_{n}}$ (Rotation), ${\displaystyle \sigma }$ (Spiegelung), ${\displaystyle S_{n}}$ (Drehspiegelung) und ${\displaystyle i}$ (Inversion oder Punktsymmetrie, die es beim Tetraeder nicht gibt). Mit dem Index ${\displaystyle n}$ werden Zähligkeiten bei Rotation und Drehspiegelung unterschieden.

Aufteilung der Kugeloberfläche in Fundamentalbereiche nach Tetraeder-Symmetrie

Volle Tetraedergruppe

Alle 7 Achsen der Rotationssymmetrie eines regulären und homogenen Tetraeders

Drei 2-zählige Achsen

Vier 3-zählige Achsen

Spiegelsymmetrieebene und Drehspiegelsymmetrieachse mit Drehspiegelebene

Eine von sechs Spiegelsymmetrieebenen

Eine von drei 4-zähligen Drehspiegelsymmetrieachsen mit Drehspiegelebene

Die Symmetrien des regulären und homogenen Tetraeders werden auch im Artikel Tetraeder erläutert. Die volle Tetraedergruppe besteht aus Drehungen, Spiegelungen und Drehspiegelungen, die das Tetraeder in sich überführen, und hat 24 Gruppenelemente. Die Gruppenordnung ist somit 24. Werden alle vier Ecken (oder alle vier Flächen) des Tetraeders durchnummeriert, so sind alle 24 möglichen Permutationen auch tatsächlich Symmetrieelemente des Tetraeders.^[2]

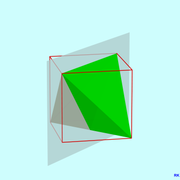
Ein solches Tetraeder besitzt insgesamt 7 Drehachsen (Achsen der Rotationssymmetrie), wie in der nebenstehenden Grafik dargestellt:

• 3 die durch Mittelpunkte gegenüberliegender Kanten und
• 4 die durch gegenüberliegende Ecken und Flächenmittelpunkte verlaufen.

Das eingezeichnete Drahtgittermodell eines umhüllenden Würfels erleichtert die Zuordnung der Drehachsen eines Tetraeders zu denen eines Würfels.

Außerdem besitzt das Tetraeder folgende Symmetrien:

• Sechs Spiegelsymmetrieebenen, die jeweils durch eine Kante und senkrecht zur gegenüberliegenden Kante verlaufen. Eine von denen ist in der ersten Grafik rechts dargestellt.
• Drei 4-zählige Drehspiegelsymmetrieachsen, die durch die Mittelpunkte gegenüberliegender Kanten verlaufen. Zu jeder Drehspiegelachse gehört eine Drehspiegelebene, die durch das Symmetriezentrum, den Mittelpunkt des Tetraeders geht und deren Normalenvektor die Drehspiegelsymmetrieachse ist. Eine der drei Drehspiegelsymmetrieachsen und die zugehörige Drehspiegelebene sind in der zweiten Grafik rechts dargestellt. Wie man aus der Grafik erkennt, ist die Drehspiegelebene keine Spiegelsymmetrieebene des Tetraeders. Jede Drehspiegelung fügt zwei Symmetrien der Tetraedergruppe hinzu.

Die volle Tetraedergruppe ist isomorph zu einer Untergruppe der Würfelgruppe (Oktaedergruppe ${\displaystyle O_{h}}$), und zwar zur Würfel-Drehgruppe (Oktaeder-Drehgruppe ${\displaystyle O}$). Seltener wird diese Tatsache so ausgedrückt: Die Würfelgruppe ist eine Übergruppe der Tetraedergruppe.

Die Tetraedergruppe ist, wie bereits erwähnt, isomorph zur Gruppe der Permutationen von vier (beliebigen) unterschiedlichen Objekten, zur symmetrischen Gruppe mit dem Symbol ${\displaystyle S_{4}}$ (das kein Schoenflies-Symbol ist).^[3] Verwenden wir die Nummern der vier Ecken der ersten Grafik des Tetraeders und ordnen die Symmetrieelemente in der zuvor gegebenen Reihenfolge (Drehungen, Spiegelungen, Drehspiegelungen), so ergibt das für die 24 Permutationen folgende Reihenfolge:

${\displaystyle T_{d}=\{1234,2143,3412,4321,1423,1342,3241,4213,4132,2431,2314,3124,}$ ${\displaystyle \qquad \quad 1243,1324,1432,2134,4231,3214,4312,3421,4123,2341,3142,2413\}}$.

Die 12 Drehungen in der ersten Zeile sind die geraden, die 12 Spiegelungen und Drehspiegelungen in der zweiten Zeile die ungeraden Permutationen.

Mit der Schoenflies-Symbolik der Elemente können die Elemente wie folgt symbolisiert werden:

${\displaystyle T_{d}=\{E,C_{2,1},C_{2,2},C_{2,3},C_{3,1},C_{3,1}^{2},C_{3,2},C_{3,2}^{2},C_{3,3},C_{3,3}^{2},C_{3,4},C_{3,4}^{2},}$ ${\displaystyle \qquad \quad \sigma _{d,1},\sigma _{d,2},\sigma _{d,3},\sigma _{d,4},\sigma _{d,5},\sigma _{d,6},S_{4,1},S_{4,1}^{3},S_{4,2},S_{4,2}^{3},S_{4,3},S_{4,3}^{3}\}}$.

Das Symbol ${\displaystyle E}$ steht für das neutrale Element. Die Symbole ${\displaystyle C_{n}}$ (Rotation), ${\displaystyle \sigma _{d}}$ (Spiegelung) und ${\displaystyle S_{n}}$ (Drehspiegelung) charakterisieren den Symmetrietyp. Der zweite Index nummeriert jeweils Elemente vom gleichen Typ durch. Zum Beispiel bedeutet ${\displaystyle C_{3,1}}$ eine dreizählige Rotation und das erste Element dieses Typs. Eine Potenz, zum Beispiel ${\displaystyle C_{3,1}^{2}}$, bedeutet das Produkt (die Verknüpfung) des Elements ${\displaystyle C_{3,1}}$ mit sich selbst, ${\displaystyle S_{4,1}^{3}}$ die dritte Potenz des Elements ${\displaystyle S_{4,1}}$.

Die Reihenfolge der Elemente können wir frei wählen. Wir machen davon Gebrauch und ordnen nun die Spiegel- und Drehspiegelsymmetrien so um, dass die Reihenfolge analog zur Reihenfolge der Drehsymmetrien ist. Wir verknüpfen dazu jedes Element der ersten 12 Symmetrien mit dem Element der ersten Spiegelsymmetrie ${\displaystyle \sigma _{d,1}}$ und verwenden die sich so ergebende Reihenfolge für die Verknüpfungstafel.^[4] Das 13. Element ist dann ${\displaystyle E*\sigma _{d,1}=\sigma _{d,1}}$, das 14. ${\displaystyle C_{2,1}*\sigma _{d,1}=\sigma _{d,4}}$ usw.

Für die Interpretation der Verknüpfungstafel in Farbe ist es außerdem von Vorteil, die Elementsymbole in dieser neuen Reihenfolge mit Farben zu unterlegen. Dabei heben wir das neutrale Element ${\displaystyle E}$ durch die Farbe Schwarz, das zweite hervorgehobene Spiegelsymmetrieelement ${\displaystyle \sigma _{d,1}}$ durch die Farbe Weiß hervor:

${\displaystyle T_{d}=\{}$ ${\displaystyle \color {white}E,}$ ${\displaystyle C_{2,1},}$ ${\displaystyle C_{2,2},}$ ${\displaystyle C_{2,3},}$ ${\displaystyle C_{3,1},}$ ${\displaystyle C_{3,1}^{2},}$ ${\displaystyle C_{3,2},}$ ${\displaystyle C_{3,2}^{2},}$ ${\displaystyle C_{3,3},}$ ${\displaystyle C_{3,3}^{2},}$ ${\displaystyle C_{3,4},}$ ${\displaystyle C_{3,4}^{2},}$

             ${\displaystyle \sigma _{d,1},}$ ${\displaystyle \sigma _{d,4},}$ ${\displaystyle S_{4,1}^{3},}$ ${\displaystyle S_{4,1},}$ ${\displaystyle \sigma _{d,3},}$ ${\displaystyle \sigma _{d,2},}$ ${\displaystyle \sigma _{d,6},}$ ${\displaystyle \sigma _{d,5},}$ ${\displaystyle S_{4,2},}$ ${\displaystyle S_{4,3}^{3},}$ ${\displaystyle S_{4,2}^{3},}$ ${\displaystyle S_{4,3}}$ ${\displaystyle \}}$.

Verknüpfungstafel

Mit einer Verknüpfungstafel oder Gruppentafel,^[5] in den Naturwissenschaften auch Gruppenmultiplikationstafel^[6] oder Gruppenmultiplikationstabelle^[7] genannt, wird das Verknüpfungsprodukt (Produkt) zweier Gruppenelemente in Gestalt einer Tabelle angeordnet. Dabei gilt die Vereinbarung, dass die in der ersten Zeile, der Kopfzeile, angeordnete Symmetrieoperation zuerst und dann die in der ersten Spalte, der Eingangsspalte, angeordnete Symmetrieoperation ausgeführt wird. Eine separate Titelzeile und Titelspalte, wie in den meisten relevanten Wikipedia-Artikeln praktiziert, ist nicht zwingend erforderlich, da sie redundant ist. Im Kreuzungspunkt von Zeile und Spalte steht das Produkt beider Elemente. Kommutieren alle Produkte (abelsche Gruppe), so ist die Tabelle (Verknüpfungstafel) symmetrisch bezüglich der Hauptdiagonalen, was bei der Tetraedergruppe aber nicht der Fall ist.

In der Grafik werden die Elemente der Tetraedergruppe durch Farbquadrate und entsprechend auch die Verknüpfungstafel in Farbe dargestellt, und zwar in der neuen Reihenfolge wie oben eingeführt. Die ersten 12 Symmetrieoperationen sind Drehungen (die zweizähligen zuerst). Diese Art der Darstellung von Verknüpfungstafeln in Farbe findet man auch in moderneren Online-Veröffentlichungen, zum Beispiel in der Online-Enzyklopädie zur Mathematik MathWorld.^[8]

Aus der Grafik Verknüpfungstafel lassen sich rein optisch folgende Schlüsse ziehen:

• Ist das Produkt eines Elements mit sich selbst das neutrale Element, so liegt das Produkt auf der Hauptdiagonalen (unter der Voraussetzung, dass in der Kopfzeile und der Eingangsspalte die Elemente in der gleichen Reihenfolge angeordnet sind). Dann ist das Element zu sich selbst invers, hat also die Elementordnung 2. Das trifft auf 9 Gruppenelemente (und das neutrale Element) zu.

Verknüpfungstafel der Tetraedergruppe T_d und der symmetrischen Gruppe S₄ in Farbe. Das neutrale Element ist schwarz, das erste Spiegelsymmetrieelement weiß

• Alle Elemente der Ordnung 2 bilden stets mit dem neutralen Element eine Untergruppe der Ordnung 2. So auch diese 9. Weitere Untergruppen der Ordnung 2 kann es nicht geben. Eine davon bilden die ersten beiden Elemente. Für zwei Elemente gibt es nur einen Gruppentyp (er kann wahlfrei mit ${\displaystyle C_{2}}$, ${\displaystyle D_{1}}$ oder ${\displaystyle S_{2}}$ symbolisiert werden).
• Die ersten vier Elemente bilden eine Untergruppe, denn die Farben ihrer Produkte bleiben in dem ersten 4x4-Block und die Farben sind bezüglich der Hauptdiagonalen symmetrisch. Diese Untergruppe ist folglich abelsch. Sie ist vom Gruppentyp Kleinsche Vierergruppe (und außerdem die einzige Untergruppe der Tetraedergruppe vom Typ Normalteiler, auf den hier nicht näher eingegangen werden soll).
• Die ersten 12 Elemente bilden ebenfalls eine Untergruppe, die aber nicht abelsch ist. Es handelt sich um die Tetraeder-Drehgruppe.
• Das Produkt von einem Rotationssymmetrieelement (Block mit den Farben Rot bis Grün) mit einem Spiegel- oder Drehspiegelsymmetrieelement (Block mit den Farben Hellblau bis Purpur) ist ein Spiegel- oder Drehspiegelsymmetrieelement und umgekehrt.
• Das Produkt von einem Spiegel- oder Drehspiegelsymmetrieelement mit einem Spiegel- oder Drehspiegelsymmetrieelement ist ein Rotationssymmetrieelement.
• Durch die Umordnung der Elemente 13 bis 24 haben wir erreicht, dass sich die Struktur des ersten Diagonalblocks im rechten Nebendiagonalblock wiederfindet, die Struktur des zweiten Diagonalblocks im linken Nebendiagonalblock.

Diese Schlussfolgerungen lassen sich im Prinzip aus jedem Typ von Verknüpfungstafeln ziehen, auch aus solchen mit Symbolen. Besonders offensichtlich werden sie aber nur in einer Verknüpfungstafel in Farbe, insbesondere dann, wenn für das neutrale Element die Farbe Schwarz gewählt wird. Um weitere Eigenschaften der Gruppe, insbesondere Klassen und alle Untergruppen aus der Verknüpfungstafel zu ermitteln, ist es bereits bei einer Gruppenordnung von 24 zweckmäßig, ein Computerprogramm zu verwenden.

Klassen

Die Elemente jeder beliebigen Gruppe werden nach Konjugationsklassen unterschieden, die in den Naturwissenschaften meist kurz Klassen genannt werden.^[9][10] Jedes Element gehört zu einer und nur einer Klasse. Bei Symmetrien einfacher geometrischer Körper ist die Zuordnung zu Klassen als Symmetrietyp (mehr oder weniger) „anschaulich“ (Drehspiegelsymmetrien ausgenommen). Bei abstrakten Gruppen höherer Ordnung ist ein Computerprogramm erforderlich, um die Klassen einer Gruppe zu ermitteln.

Die Anzahl der Klassen ist gleich der Anzahl der irreduziblen Darstellungen der Gruppe durch Matrizen, die für Anwendungen in der Physik besonders wichtig sind.^[11]

Die Tetraedergruppe besteht aus 5 Klassen. Die Anzahl der Klassen nennt man, analog zu Gruppenordnung, die Klassenordnung der Gruppe, die hier somit 5 ist. Das sind: Die triviale Klasse mit dem neutralen Element ${\displaystyle E}$, 3 Elemente vom Symmetrietyp ${\displaystyle C_{2}}$ (Rotation), 8 Elemente vom Typ ${\displaystyle C_{3}}$ (Rotation), 6 Elemente vom Typ ${\displaystyle \sigma _{d}}$ (Spiegelung) und 6 Elemente vom Typ ${\displaystyle S_{4}}$^[12] (Drehspiegelung).^[13]

Untergruppen

Die volle Tetraedergruppe hat (die vollständige Gruppe nicht gezählt) 29 Untergruppen:

1 Triviale Gruppe ${\displaystyle :\;\{E\}}$

3 Zyklische Gruppen ${\displaystyle C_{2}:\;\{E,C_{2,1}\},\{E,C_{2,2}\},\{E,C_{2,3}\}}$

6 Diedergruppen ${\displaystyle D_{1}:\;\{E,\sigma _{d,1}\},\{E,\sigma _{d,2}\},\{E,\sigma _{d,3}\},\{E,\sigma _{d,4}\},\{E,\sigma _{d,5}\},\{E,\sigma _{d,6}\}}$

4 Zyklische Gruppen ${\displaystyle C_{3}:\;\{E,C_{3,1},C_{3,1}^{2}\},\{E,C_{3,2},C_{3,2}^{2}\},\{E,C_{3,3},C_{3,3}^{2}\},\{E,C_{3,4},C_{3,4}^{2}\}}$

1 Kleinsche Vierergruppe ${\displaystyle V:\;\{E,C_{2,1},C_{2,2},C_{2,3}\}}$

3 Diedergruppen ${\displaystyle D_{2}:\;\{E,C_{2,1},\sigma _{d,1},\sigma _{d,4}\},\{E,C_{2,2},\sigma _{d,3},\sigma _{d,6}\},\{E,C_{2,3},\sigma _{d,2},\sigma _{d,5}\}}$

3 Drehspiegelgruppen ${\displaystyle S_{4}:\;\{E,C_{2,1},S_{4,1},S_{4,1}^{3}\},\{E,C_{2,2},S_{4,2},S_{4,2}^{3}\},\{E,C_{2,3},S_{4,3},S_{4,3}^{3}\}}$

4 Diedergruppen ${\displaystyle D_{3}:\;\{E,C_{3,1},C_{3,1}^{2},\sigma _{d,1},\sigma _{d,2},\sigma _{d,3}\},\{E,C_{3,2},C_{3,2}^{2},\sigma _{d,1},\sigma _{d,5},\sigma _{d,6}\},}$ ${\displaystyle \qquad \qquad \qquad \qquad \quad \{E,C_{3,3},C_{3,3}^{2},\sigma _{d,3},\sigma _{d,4},\sigma _{d,5}\},\{E,C_{3,4},C_{3,4}^{2},\sigma _{d,2},\sigma _{d,4},\sigma _{d,6}\}}$

3 Diedergruppen ${\displaystyle D_{4}:\;\{E,C_{2,1},C_{2,2},C_{2,3},\sigma _{d,1},\sigma _{d,4},S_{4,1},S_{4,1}^{3}\},\{E,C_{2,1},C_{2,2},C_{2,3},\sigma _{d,2},\sigma _{d,5},S_{4,2},S_{4,2}^{3}\},}$ ${\displaystyle \qquad \qquad \qquad \qquad \quad \{E,C_{2,1},C_{2,2},C_{2,3},\sigma _{d,3},\sigma _{d,6},S_{4,3},S_{4,3}^{3}\}}$

1 Tetraeder-Drehgruppe ${\displaystyle T:\;\{E,C_{2,1},C_{2,2},C_{2,3},C_{3,1},C_{3,1}^{2},C_{3,2},C_{3,2}^{2},C_{3,3},C_{3,3}^{2},C_{3,4},C_{3,4}^{2}\}}$

Von diesen sind nur die triviale Untergruppe und die Kleinsche Vierergruppe vom Typ Normalteiler.

Körper mit voller Tetraeder-Symmetrie

Typ	Name	Bild	Flächen	Ecken	Kanten
Platonischer Körper	Tetraeder		4	4	6
Archimedischer Körper	Tetraederstumpf		8	12	18
Catalanischer Körper	Triakistetraeder		12	8	18
Beinahe-Johnson-Körper[14]	Triakistetraederstumpf[15]		16	28	42
	Tetrated dodecahedron[16]		28	28	54
Regulärer Sternkörper[17]	Tetrahemihexaeder[18]		7	6	12

Tetraeder-Drehgruppe

→ Hauptartikel: A4 (Gruppe)

Darstellung der Tetraeder-Drehgruppe als Zykel-Graph

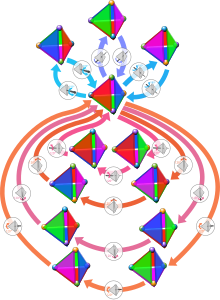
Ein reguläres und homogenes Tetraeder besitzt 7 Rotationsachsen und ist invariant gegenüber 11 verschiedenen Rotationen um diese Achsen. Die Gruppe der Drehungen des Tetraeders, die Tetraeder-Drehgruppe ${\displaystyle T}$, besitzt folglich (das neutrale Element mitgezählt) 12 Elemente. Sie ist die einzige Untergruppe der Tetraedergruppe ${\displaystyle T_{d}}$ der Ordnung 12. Die Verknüpfungstafel der Tetraeder-Drehgruppe ist identisch mit dem ersten 12x12-Block (mit den Farben Rot bis Grün) der Verknüpfungstafel der vollen Tetraedergruppe oben.

Die Tetraeder-Drehgruppe ist nicht abelsch. Sie ist isomorph zur alternierenden Gruppe ${\displaystyle A_{4}}$, die im Artikel A4 (Gruppe) beschrieben wird. Die Elemente werden dort durch fortlaufende Buchstaben, gegebenenfalls mit Indizes und Potenzen, symbolisiert:

${\displaystyle A_{4}=\left\{e,a,b,c,d_{1},d_{1}^{2},d_{2},d_{2}^{2},d_{3},d_{3}^{2},d_{4},d_{4}^{2}\right\}}$.

In der Schoenflies-Symbolik der Elemente entspricht das den folgenden Elementen:

${\displaystyle T=\left\{E,C_{2,1},C_{2,2},C_{2,3},C_{3,1},C_{3,1}^{2},C_{3,2},C_{3,2}^{2},C_{3,3},C_{3,3}^{2},C_{3,4},C_{3,4}^{2}\right\}}$.

Im Hauptartikel ist auch eine Grafik des Tetraeders und die Zuordnung der Gruppenelemente zu Permutationen (der vier Ecken des Tetraeders) dargestellt sowie die beiden prinzipiell verschiedenen Typen von Rotationsachsen (Kantenmitte zu Kantenmitte oder Ecke zu Flächenmitte). Außerdem werden zwei Arten der Verknüpfungstafeln dieser Gruppe wiedergegeben, eine, bei der die Elemente und ihre Produkte durch Buchstaben und Zahlen symbolisiert werden, und eine zweite durch Farbquadrate.

Die Grafik stellt die Elemente der Tetraeder-Drehgruppe als Zykel-Graph dar. Ausgangs- und Endpunkt aller Pfeile ist das neutrale Element. Die drei zweizähligen Rotationen (um Kantenmitten) werden als blaue Pfeile und die vier dreizähligen als rötliche Pfeile dargestellt. Die Einfärbung der Flächen der Tetraeder dient dabei lediglich der Veranschaulichung der Symmetrieoperationen, denn ein Tetraeder, dessen Seitenflächen so wie in der Grafik eingefärbt sind, besitzt keine Symmetrien.

Klassen

Die Tetraeder-Drehgruppe besteht aus 4 Klassen (alle vom Symmetrietyp Rotation). Das sind: Die triviale Klasse mit dem neutralen Element ${\displaystyle E}$, 3 Elemente vom Typ ${\displaystyle C_{2}}$ (in der Grafik Zykel-Graph sind damit die drei oberen Tetraeder gemeint), 4 Elemente vom Typ ${\displaystyle C_{3}}$ (die vier rechten unteren) und 4 Elemente vom Typ ${\displaystyle C_{3}^{2}}$ (die vier linken unteren).

Untergruppen

Die Tetraeder-Drehgruppe hat (wieder die vollständige Gruppe nicht gezählt) 9 Untergruppen: Die triviale Untergruppe der Ordnung 1, drei der Ordnung 2, 4 der Ordnung 3 und eine der Ordnung 4.^[19] Welche Elemente zu welcher Untergruppe gehören, ist im Hauptartikel zu finden. Auch bei der Tetraeder-Drehgruppe sind nur die triviale Untergruppe und die Untergruppe der Ordnung 4 vom Typ Normalteiler.

Die Tetraeder-Drehgruppe hat keine Untergruppe der Ordnung 6, obwohl eine solche dem Satz von Lagrange (Ordnung der Untergruppe ist Teiler der Ordnung der Gruppe) nicht widersprechen würde.

Verwandter Gruppentyp

Ergänzend sei angemerkt, dass es eine Gruppe der oben erwähnten 12 nichtabelschen Gruppentypen der Ordnung 24 mit dem Schoenflies-Symbol ${\displaystyle T_{h}}$ gibt.^[20] Diese hat 8 Klassen. Das sind: Die triviale Klasse mit dem neutralen Element, 4 Elemente vom Typ ${\displaystyle C_{3}}$, 4 Elemente vom Typ ${\displaystyle C_{3}^{2}}$, 3 Elemente vom Typ ${\displaystyle C_{2}}$, ein Element vom Typ ${\displaystyle i}$ (Inversion), 4 Elemente vom Typ ${\displaystyle S_{6}}$ (Drehspiegelung), 4 Elemente vom Typ ${\displaystyle S_{6}^{5}}$ und 3 Elemente vom Typ ${\displaystyle \sigma _{h}}$(Spiegelung).^[21]

Die ${\displaystyle T_{h}}$ kann erzeugt werden durch ${\displaystyle T}$ ∪ {${\displaystyle i}$} also durch Adjunktion der Inversion (${\displaystyle -id\in \mathbb {R} ^{3}}$) zur ${\displaystyle T}$. Im Gegensatz zu den Drehgruppen der anderen platonischen Körper führt die Hinzufügung der Inversion nicht zur vollen symmetrischen Gruppe. Die ${\displaystyle T_{d}}$ ist somit inversionsfrei. Anschaulich gesehen liegt das daran, dass der Tetraeder der einzige platonische Körper ist, der keine parallel gegenüberliegenden Flächen hat. Die ${\displaystyle T_{h}}$ ist Untergruppe der ${\displaystyle O_{h}}$. Ein Körper, der die ${\displaystyle T_{h}}$ als Symmetriegruppe hat wäre zum Beispiel ein Würfel, dessen Flächen durch eine Diagonale geteilt sind. Damit sind die 90°-Drehungen und 6 Spiegelungen sowie 6 180° Drehungen der ${\displaystyle O_{h}}$ ausgeschlossen, was zur ${\displaystyle T_{h}}$ führt.

Siehe auch

• Oktaedergruppe
• Ikosaedergruppe
• Polyeder
• Platonischer Körper
• Tetraeder

Literatur

• Arthur Schoenflies: Krystallsysteme und Krystallstructur. Teubner, Leipzig 1891 (XII, 638 S., Online-Ressourcen). 
• John S. Lomont: Applications of finite groups. Reprint Auflage. Dover Publications, New York 1993, ISBN 0-486-67376-6 (XI, 346 S., Reprint der Auflage: Academic Press, New York 1959). 
• Henry Margenau, George Moseley Murphy: Die Mathematik für Physik und Chemie: Band I. Kapitel XV. Gruppentheorie. Teubner, Leipzig 1964 (724 S.). 
• Arthur P. Cracknell: Angewandte Gruppentheorie. Akademie-Verlag [u. a.], Berlin 1971, ISBN 3-528-06084-0 (453 S.). 
• Harold Scott MacDonald Coxeter: Regular polytopes. 3. ed., unabridged and corr. repr. of the 2. ed., New York, Macmillan, 1963. Dover Publications, New York 1973, ISBN 0-486-61480-8 (XIII, 321 S., eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 25. Januar 2020] Die Vorschau enthält keine Seitennummerierung). 
• Frank Albert Cotton: Chemical applications of group theory. 3. ed. Wiley, New York, NY 1990, ISBN 0-471-51094-7 (XIV, 461 S.). 

Weblinks

• Tetrahedral Group, Mathworld
• Tetraedergruppe und symmetrische Gruppe S₄
• Symmetric group S₄

Einzelnachweise

1. Schoenflies 1891, S. 74 und S. 102, Gruppentypen werden von Schoenflies Krystallclassen genannt. Er nennt die triviale Gruppe, die nur aus dem neutralen Element besteht, Identität und symbolisiert sie mit ${\displaystyle C_{1}}$.
2. Werden zum Beispiel die sechs Flächen eines Würfels wie beim Spielwürfel nummeriert, sind keineswegs alle 720 möglichen Permutationen auch Symmetrieelemente des Würfels.
3. Es handelt sich um ein Symbol der abstrakten Gruppentheorie, desjenigen Zweigs der Gruppentheorie, der Symmetrien ohne direkten Bezug auf geometrische Körper behandelt.
4. Bei inversionssymmetrischen Körpern, beim Würfel zum Beispiel, wird man die Drehsymmetrien mit der Inversion verknüpfen.
5. B. L. van der Waerden: Moderne Algebra. 3. verbesserte Auflage. Springer-Verlag, Berlin, Göttingen, Heidelberg 1950, S. 24 (VIII, 292). 
6. Cracknell 1971, S. 16.
7. Margenau 1964, S. 664.
8. MathWorld: Tetrahedral Group Man beachte folgende Unterschiede: In der oben wiedergegebenen Farbgrafik der Verknüpfungstafel wird das neutrale Element als schwarzes Quadrat hervorgehoben, was in der Farbgrafik in MathWorld nicht der Fall ist. Außerdem ist die Reihenfolge der Elemente eine andere. Auf der MathWorld-Site ist nicht angegeben, welche Reihenfolge für die Farbgrafik gewählt wurde.
9. Cracknell 1971, S. 24 ff.
10. Margenau 1964, S. 665 f.
11. Cracknell 1971, S. 36 ff.
12. Man beachte, dass hier mit dem Symbol ${\displaystyle S_{4}}$ ein Symbol der Schoenflies-Symbolik gemeint ist. Das Symbol ${\displaystyle S_{4}}$ als Symbol einer speziellen symmetrischen Gruppe gehört nicht zur Schoenflies-Symbolik. Was mit dem Symbol jeweils gemeint ist, sollte aus dem Kontext erschließbar sein.
13. Cotton 1990, S. 47 und S. 434.
14. Konvexe Polyeder, deren Flächen fast reguläre Polygone sind, von denen einige oder alle nicht genau regelmäßig sind. Verwandt mit den Johnson-Körpern, siehe Near-miss Johnson solid.
15. Englischer Name Truncated triakis tetrahedron.
16. Deutscher Name unbekannt. Deshalb ist in der Tabelle der englische Name Tetrated dodecahedron aufgeführt.
17. Ein nichtkonvexer regulärer Körper. Deshalb gilt der Eulersche Polyedersatz nicht.
18. Englischer Name Tetrahemihexahedron.
19. Cotton 1990, S. 50 und S. 433.
20. Schoenflies 1891, S. 102.
21. Cotton 1990, S. 50 und S. 434.