Γωνίες Όιλερ

Γεωμετρικός ορισμός των κλασσικών γωνιών Euler. Το (σταθερό) σύστημα συντεταγμένων xyz εμφανίζεται με μπλε χρώμα, ενώ το (περιστραμμένο) σύστημα XYZ εμφανίζεται με κόκκινο χρώμα. Η γραμμή των κόμβων ( N ) εμφανίζεται με πράσινο χρώμα

Οι γωνίες Euler είναι τρεις γωνίες που εισήγαγε ο Leonhard Euler για να περιγράψουν τον προσανατολισμό ενός στερεού σώματος σε σχέση με ένα σταθερό σύστημα συντεταγμένων .^[1]

Στη φυσική μπορούν επίσης να αντιπροσωπεύουν τον προσανατολισμό ενός κινητού συστήματος αναφοράς ή τον προσανατολισμό μιας γενικής βάσης στην τρισδιάστατη γραμμική άλγεβρα. Αργότερα εισήχθησαν από τους Peter Guthrie Tait και George H. Bryan εναλλακτικές μορφές, που προορίζονται για χρήση στην αεροναυτική και τη μηχανική.

Ισοδυναμία διαδοχικών περιστροφών

Μπορούμε να μεταβούμε σε οποιοδήποτε προσανατολισμό, ξεκινώντας από έναν γνωστό προσανατολισμό αναφοράς, και χρησιμοποιώντας μία ειδική ακολουθία ενδογενών περιστροφών, που οι τιμές τους είναι οι γωνίες Euler του τελικού προσανατολισμού. Το παράδειγμα αυτό χρησιμοποιεί την ακολουθία z-x′-z″.

Οι γωνίες Euler μπορούν να καθοριστούν με στοιχειώδη γεωμετρία ή με σύνθεση περιστροφών. Ο γεωμετρικός ορισμός δείχνει ότι τρεις στοιχειώδεις περιστροφές (περιστροφές γύρω από τους άξονες ενός συστήματος συντεταγμένων) είναι πάντοτε επαρκείς για την μετακίνηση ενός συστήματος συντεταγμένων (ή ενός στερεού σώματος, πάνω στο οποίο μπορεί να είναι στερεά προσδεμένο) σε οποιοδήποτε επιθυμητό προσανατολισμό.

Οι τρεις στοιχειώδεις περιστροφές μπορεί να είναι ή εξωγενείς (περιστροφές γύρω από τους άξονες xyz του αρχικού συστήματος συντεταγμένων, που υποτίθεται ότι παραμένει ακίνητο), ή ενδογενείς (περιστροφές γύρω από τους άξονες του περιστρεφόμενου συστήματος συντεταγμένων XYZ, που είναι στερεωμένο πάνω στο κινούμενο σώμα και το οποίο και αλλάζει προσανατολισμό, μετά από κάθε στοιχειώδη περιστροφή. Το σύστημα αυτό μερικές φορές αναφέρεται σαν τοπικό σύστημα).

Οι γωνίες Euler συμβολίζονται συνήθως ως α, β, γ, ή ως φ, θ, ψ . Διάφοροι συγγραφείς, για να ορίσουν τις γωνίες Euler, μπορεί να χρησιμοποιούν διαφορετικά σύνολα αξόνων περιστροφής ή και διαφορετικά ονόματα για τις ίδιες γωνίες. Επομένως, πριν από κάθε συζήτηση που χρησιμοποιεί τις γωνίες Euler, πρέπει πάντα να προηγείται ο ορισμός τους.

Χωρίς να εξετάσουμε τη δυνατότητα χρήσης δύο διαφορετικών συμβάσεων για τον ορισμό των αξόνων περιστροφής (ενδογενών ή εξωγενών), υπάρχουν δώδεκα πιθανές ακολουθίες αξόνων περιστροφής, χωρισμένες σε δύο ομάδες:

• Κύριες γωνίες Euler (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y)
• Γωνίες Tait – Bryan (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z) .

Οι γωνίες Tait – Bryan ονομάζονται επίσης:

• γωνίες Cardan,
• ναυτικές γωνίες,
• πορεία (heading), ανύψωση (elevation) και στροφή (bank) ή
• yaw (εκτροπή), pitch (ανύψωση), και roll (κύλιση).

Μερικές φορές, και τα δύο είδη ακολουθιών ονομάζονται "γωνίες Euler". Σε αυτήν την περίπτωση, οι ακολουθίες της πρώτης ομάδας ονομάζονται κύριες ή κλασικές γωνίες Euler.

Κύριες γωνίες Euler

 

"Αριστερά": Ένα γυροσκόπιο που δείχνει την ακολουθία περιστροφών z-x-z. Το εξωτερικό σύστημα αναφοράς φαίνεται στη βάση. Οι εσωτερικοί άξονες είναι κόκκινοι. "Δεξιά": Ένα απλό διάγραμμα που εμφανίζει τις ίδιες γωνίες Euler σε ένα διάγραμμα.

Γεωμετρικός ορισμός

Οι άξονες του αρχικού συστήματος συντεταγμένων συμβολίζονται ως x, y, z, ενώ οι άξονες του περιστραμμένου συστήματος συντεταγμένων ως X, Y, Z.

Ο γεωμετρικός ορισμός (μερικές φορές αναφέρεται ως στατικός) ξεκινά με τον καθορισμό της γραμμής των κόμβων Ν ως της τομής των επιπέδων xy και XY (μπορεί επίσης να οριστεί ως η κοινή κάθετη στους άξονες z και Z, και τότε γράφεται ως το διανυσματικό γινόμενο -εξωτερικό γινόμενο- N = z ${\displaystyle \times }$ Ζ ). Χρησιμοποιώντας την γραμμή των κόμβων, οι τρεις γωνίες Euler μπορούν να οριστούν ως εξής:

• ${\displaystyle \alpha }$ (ή ${\displaystyle \varphi }$ ) είναι η γωνία μεταξύ του άξονα x και του άξονα Ν (x -σύμβαση, θα μπορούσε επίσης να οριστεί ως η γωνία μεταξύ y και N, που ονομάζεται y -σύμβαση).
• ${\displaystyle \beta }$ (ή ${\displaystyle \theta \,}$ ) είναι η γωνία μεταξύ του άξονα z και του άξονα Z.
• ${\displaystyle \gamma }$ (ή ${\displaystyle \psi }$ ) είναι η γωνία μεταξύ του άξονα Ν και του άξονα X (x -σύμβαση, ή ως η γωνία μεταξύ Y και του N, y -σύμβαση).

Οι γωνίες Euler μεταξύ δύο συστημάτων αναφοράς ορίζονται, μόνο εάν και τα δύο συστήματα έχουν τον ίδιο προσανατολισμό (δηλ. είναι και τα δύο δεξιόστροφα ή και τα δύο αριστερόστροφα).

Συμβάσεις στις ενδογενείς περιστροφές

Οι ενδογενείς περιστροφές είναι στοιχειώδεις περιστροφές που γίνονται γύρω από τους άξονες του (κινούμενου) συστήματος συντεταγμένων XYZ,, που είναι σταθερά συνδεμένο με το κινούμενο σώμα. Επομένως οι άξονες αυτοί, αλλάζουν τον προσανατολισμό τους μετά από κάθε στοιχειώδη περιστροφή. Το σύστημα XYZ περιστρέφεται, ενώ το xyz είναι σταθερό. Ξεκινώντας με το XYZ να ταυτίζεται αρχικά με το xyz, μπορεί να χρησιμοποιηθεί μια ακολουθία τριών ενδογενών περιστροφών για την επίτευξη οποιουδήποτε επιθυμητού προσανατολισμού του XYZ .

Οι γωνίες του Euler μπορούν να καθοριστούν με ενδογενείς περιστροφές. Το περιστρεφόμενο σύστημα αναφορά XYZ, μπορούμε να το φανταστούμε να ταυτίζεται αρχικά με το ακίνητο xyz. Για να φτάσει στην τελική του θέση θα γίνουν τρεις περιστροφές γύρω από τους άξονές του, και κάθε φορά γύρω από τη νέα τους θέση. Οι τρεις διαδοχικές του θέσεις μέχρι να φτάσει στην τελική του θέση, μπορούν να συμβολιστούν ως εξής:

• x-y-z, ή x₀-y₀-z₀ (θέση 0-αρχικό)
• x′-y′-z′ ή x₁-y₁-z₁ (θέση 1-μετά την πρώτη περιστροφή)
• x ″-y ″-z ″ ή x₂-y₂-z₂ (θέση 2-μετά τη δεύτερη περιστροφή)
• X-Y-Z ή x₃-y₃-z ₃ (θέση 3-τελική)

Για την παραπάνω αναφερόμενη ακολουθία περιστροφών, η γραμμή των κόμβων Ν μπορεί απλά να οριστεί ως η διεύθυνση του Χ μετά την πρώτη στοιχειώδη περιστροφή. Ως εκ τούτου, το Ν μπορεί να συμβολίζεται απλά x′. Επιπλέον, δεδομένου ότι η τρίτη στοιχειώδης περιστροφή συμβαίνει γύρω από το Ζ, δεν αλλάζει τον προσανατολισμό του Ζ. Ως εκ τούτου, το Z συμπίπτει με το z″. Αυτό μας επιτρέπει να απλοποιήσουμε τον ορισμό των γωνιών Euler ως εξής:

• α (ή ${\displaystyle \varphi }$ ) αντιπροσωπεύει μια περιστροφή γύρω από τον άξονα z ,
• β (ή ${\displaystyle \theta }$ ) αντιπροσωπεύει μια περιστροφή γύρω από τον άξονα x',
• γ (ή ${\displaystyle \psi }$ ) αντιπροσωπεύει μια περιστροφή γύρω από τον άξονα z ″.

Συμβάσεις στις εξωγενείς περιστροφές

Οι εξωγενείς περιστροφές είναι στοιχειώδεις περιστροφές που γίνονται γύρω από τους άξονες του σταθερού (ακίνητου) συστήματος συντεταγμένων xyz. Δηλ. το σύστημα XYZ περιστρέφεται, ενώ το xyz παραμένει σταθερό. Ξεκινώντας με το XYZ να επικαλύπτει αρχικά το xyz, μπορεί να χρησιμοποιηθεί μια ακολουθία τριών εξωγενών περιστροφών για την επίτευξη οποιουδήποτε επιθυμητού προσανατολισμού-στόχου για το XYZ. Οι γωνίες Euler ή Tait – Bryan (α, β, γ) είναι τα μεγέθη αυτών των στοιχειωδών περιστροφών. Για παράδειγμα, ο προσανατολισμός στόχος μπορεί να επιτευχθεί ως εξής:

• Το σύστημα XYZ περιστρέφεται γύρω από τον άξονα z κατά γωνία γ. Ο άξονας X είναι τώρα σε γωνία γ σε σχέση με τον άξονα x.
• Το σύστημα XYZ περιστρέφεται ξανά γύρω από τον άξονα x κατά γωνία β. Ο άξονας Ζ είναι τώρα στη γωνία β σε σχέση με τον άξονα z .
• Το σύστημα XYZ περιστρέφεται για τρίτη φορά γύρω από τον άξονα z με α .

Ανακεφαλαιώνοντας, οι τρεις στοιχειώδεις περιστροφές συμβαίνουν γύρω από τα z, x και z του ακίνητου συστήματος συντεταγμένων. Αυτή η ακολουθία δηλώνεται συχνά ως z - x - z (ή 3-1-3). Τα σύνολα αξόνων περιστροφής που σχετίζονται τόσο με τις κύριες γωνίες Euler, όσο και με τις γωνίες Tait-Bryan ονομάζονται συνήθως χρησιμοποιώντας αυτήν την σημειογραφία (βλ. παραπάνω για λεπτομέρειες).

Πρόσημα, περιοχές τιμών και συμβάσεις

The principal axes of an aircraft according to the air norm DIN 9300. Notice that fixed and mobile frames must be coincident with angles zero. Therefore, this norm would force also a compatible axes convention in the reference system

Οι γωνίες συνήθως ορίζονται σύμφωνα με τον κανόνα του δεξιού χεριού . Δηλαδή όταν κοιτάζουμε προς τη θετική κατεύθυνση του άξονα, όταν αντιπροσωπεύουν μια περιστροφή που εμφανίζεται κατά τη φορά των δεικτών του ρολογιού (ωρολογιακή φορά - CW) έχουν θετικές τιμές, ενώ όταν η περιστροφή είναι αντίθετη από τη φορά των δεικτών του ρολογιού (αντιωρολογιακή φορά- CCW) έχουν αρνητικές τιμές . Η αντίθετη σύμβαση (κανόνας του αριστερού) ακολουθείται λιγότερο συχνά.

Σχετικά με τις εύρος (περιοχή) τιμών που μπορούν να πάρουν οι γωνίες (χρησιμοποιώντας συμβολισμό διαστήματος) ισχύουν τα εξής:

• για τις α (φ) και γ (ψ), το εύρος ορίζεται σε modulo 2π ακτίνια. Για παράδειγμα, ένα έγκυρο εύρος μπορεί να είναι [−π, π].
• για την β, το εύρος καλύπτει π ακτίνια (αλλά δεν μπορεί να θεωρηθεί ότι είναι modulo π). Για παράδειγμα, θα μπορούσε να είναι [0, π] ή [−π/2, π/2] .

Οι γωνίες α, β και γ καθορίζονται με μοναδικό τρόπο, εκτός από την ειδική περίπτωση που τα επίπεδα xy και XY ταυτίζονται. Τότε οι άξονες z και Z έχουν τις ίδιες ή αντίθετες κατευθύνσεις. Πράγματι, εάν ο άξονας z και ο άξονας Z έχουν τις ίδιες κατευθύνσεις, τότε β=0 και μόνο το (α+γ) ορίζεται μοναδικά (όχι οι μεμονωμένες τιμές) και, ομοίως, εάν ο άξονας z και ο άξονας Z είναι αντίθετοι, β=π και μόνο το (α−γ) ορίζεται μοναδικά (όχι οι μεμονωμένες τιμές). Αυτές οι ασάφειες είναι γνωστές στις εφαρμογές ως κλείδωμα του gimbal.

Υπάρχουν έξι δυνατότητες επιλογής των αξόνων περιστροφής (για κάθε τύπο ακολουθιών περιστροφής δηλ. ενδογενείς ή εξωγενείς) για τις κύριες γωνίες Euler. Σε όλες, ο πρώτος και ο τρίτος άξονας περιστροφής είναι οι ίδιοι. Οι έξι πιθανές ακολουθίες είναι:

1. z₁-x ′- z₂ ″ (ενδογενείς περιστροφές) ή z₂-x-z₁ (εξωγενείς περιστροφές)
2. x₁-y ′- x₂ ″ (ενδογενείς περιστροφές) ή x₂-y-x₁ (εξωγενείς περιστροφές)
3. y₁-z ′- y₂ ″ (ενδογενείς περιστροφές) ή y₂-z-y₁ (εξωγενείς περιστροφές)
4. z₁-y ′- z₂ ″ (ενδογενείς περιστροφές) ή z₂-y-z₁ (εξωγενείς περιστροφές)
5. x₁-z ′- x₂ ″ (ενδογενείς περιστροφές) ή x₂-z-x₁ (εξωγενείς περιστροφές)
6. y₁-x ′- y₂ ″ (ενδογενείς περιστροφές) ή y₂-x-y₁ (εξωγενείς περιστροφές)

Μετάπτωση (precession), κλόνηση (nutation) και ενδογενής περιστροφή

Βασικές κινήσεις του Euler της Γης. Ενδογενής (πράσινο),Μετάπτωση (μπλε) και Κλόνηση (κόκκινο)

Η μετάπτωση, η κλόνηση και η εγγενής περιστροφή (περιστροφή) ορίζονται ως οι κινήσεις που επιτυγχάνονται αλλάζοντας μία από τις γωνίες του Euler και αφήνοντας τις άλλες δύο αμετάβλητες. Αυτές οι κινήσεις δεν εκφράζονται ως προς το εξωτερικό σύστημα συντεταγμένων, ούτε ως προς το κινούμενο περιστρεφόμενο σύστημα συντεταγμένων του σώματος, αλλά σε μείγμα. Αποτελούν μικτούς άξονες του συστήματος περιστροφής, όπου η πρώτη γωνία μετακινεί τη γραμμή των κόμβων γύρω από τον εξωτερικό άξονα z, η δεύτερη περιστρέφεται γύρω από τη γραμμή των κόμβων N και η τρίτη είναι μια εγγενής περιστροφή γύρω από το Z, έναν άξονα στερεωμένο στο κινούμενο σώμα .

Ο στατικός ορισμός υπονοεί ότι:

• Το α (μετάπτωση) αντιπροσωπεύει μια περιστροφή γύρω από τον άξονα z ,
• Το β (κλόνηση) αντιπροσωπεύει μια περιστροφή γύρω από τον άξονα N ή x',
• γ (ενδογενής περιστροφή) αντιπροσωπεύει μια περιστροφή γύρω από τον άξονα Z ή z″.

Εάν το β είναι μηδέν, δεν υπάρχει περιστροφή γύρω από το Ν.Σαν αποτέλεσμα, το Ζ συμπίπτει με τα z, α και γ αντιπροσωπεύουν περιστροφές για τον ίδιο άξονα ( z ), και ο τελικός προσανατολισμός μπορεί να επιτευχθεί με μία μόνο περιστροφή γύρω από το z, με γωνία ίση με α + γ .

Για παράδειγμα, σκεφτείτε μια σβούρα. Η σβούρα περιστρέφεται γύρω από τον άξονά συμμετρίας της. Αυτό αντιστοιχεί στην εγγενή περιστροφή της. Περιστρέφεται επίσης γύρω από τον κεντρικό άξονά της, με το κέντρο μάζας του να περιστρέφεται γύρω περιστροφικό άξονα. αυτή η περιστροφή είναι μια προϋπόθεση. Τέλος, η σβούρα μπορεί να ταλαντεύεται πάνω-κάτω. η γωνία κλίσης είναι η γωνία κλόνησης. Το ίδιο παράδειγμα μπορεί να φανεί και με τις κινήσεις της γης.

Αν και και οι τρεις κινήσεις μπορούν να αναπαρασταθούν από έναν τελεστή περιστροφής με σταθερούς συντελεστές σε κάποιο σύστημα αναφοράς, δεν μπορούν να αναπαρασταθούν από αυτούς τους τελεστές ταυτόχρονα. Λαμβάνοντας υπόψη ένα πλαίσιο αναφοράς, το πολύ το ένα από αυτά θα είναι χωρίς συντελεστές. Μόνο η μετάπτωση μπορεί να εκφραστεί γενικά ως πίνακας στη βάση του χώρου χωρίς εξαρτήσεις από τις άλλες γωνίες.

Αυτές οι κινήσεις συμπεριφέρονται επίσης ως ένα gimbal σύνολο. Αν υποθέσουμε ότι ένα σύνολο πλαισίων, ικανό να κινείται το καθένα σε σχέση με το πρώτο σύμφωνα με μία μόνο γωνία, όπως ένα gimbal, θα υπάρχει ένα εξωτερικό σταθερό πλαίσιο, ένα τελικό πλαίσιο και δύο πλαίσια στη μέση, τα οποία ονομάζονται "ενδιάμεσα" πλαίσια". Τα δύο στη μέση λειτουργούν ως δύο δακτύλιοι gimbal που επιτρέπουν στο τελευταίο πλαίσιο να φτάσει σε οποιοδήποτε προσανατολισμό στο χώρο.

Γωνίες Τέιτ–Μπράιαν

Γωνίες Τέιτ–Μπράιαν. Ακολουθία z-y′-x" (ενδογενείς περιστροφές. Ο N συμπίπτει με τον άξονα y'). Η ακολουθία γωνιών περιστροφής είναι ψ, θ, φ . Σημειώστε ότι σε αυτήν την περίπτωση η ψ > 90° και η θ είναι αρνητική γωνία.

Η δεύτερη μορφή τυποποίησης, ονομάζεται γωνίες Τέιτ–Μπράιαν, από τους Τέιτ–Μπράιαν και τον Τζορτζ Χ. Μπράιαν. Αυτή η σύμβαση χρησιμοποιείται συνήθως σε αεροδιαστημικές εφαρμογές. Σε αυτήν η μηδενική γωνία ανύψωσης αντιπροσωπεύει την οριζόντια θέση. Οι γωνίες Τέιτ–Μπράιαν αντιπροσωπεύουν τον προσανατολισμό του αεροσκάφους σε σχέση με το παγκόσμιο σύστημα συντεταγμένων. Όταν ασχολείστε με άλλα οχήματα, είναι δυνατές διαφορετικές συμβάσεις αξόνων .

Ορισμοί

Γωνίες Tait – Bryan. z-x′-y ′ ακολουθία (εγγενείς περιστροφές. Το N συμπίπτει με x ′)

Οι ορισμοί και οι συμβολισμοί που χρησιμοποιούνται για τις γωνίες Τέιτ–Μπράιαν, είναι παρόμοιοι με εκείνους που αναφέρονται παραπάνω για τις κύριες γωνίες Όιλερ (γεωμετρικός ορισμός, ορισμός ενδογενούς περιστροφής, ορισμός εξωγενούς περιστροφής). Η μόνη διαφορά είναι ότι οι γωνίες Τέιτ–Μπράιαν αντιπροσωπεύουν περιστροφές γύρω από τρεις διαφορετικούς άξονες (π.χ. x-y-z ή x-y′-z″), ενώ οι κύριες γωνίες Όιλερ χρησιμοποιούν τον ίδιο άξονα, τόσο για την πρώτη, όσο και για την τρίτη στοιχειώδη περιστροφή (π.χ. z-x-z ή z-x′-z″).

Αυτό συνεπάγεται διαφορετικό ορισμό για τη γραμμή των κόμβων στο γεωμετρικό ορισμό. Στην περίπτωση των κύριων γωνιών Όιλερ, η γραμμή των κόμβων ορίστηκε ως η τομή μεταξύ δύο ομόλογων καρτεσιανών επιπέδων (δηλ. παράλληλων επιπέδων, όταν οι γωνίες Όιλερ είναι μηδέν, π.χ. τα xy και XY). Στην περίπτωση γωνιών Τέιτ–Μπράιαν, η γραμμή των κόμβων ορίζεται ως η τομή δύο μη ομόλογων επιπέδων (δηλ. κάθετων επιπέδων, όταν οι γωνίες Euler είναι μηδέν, π.χ. τα xy και YZ).

Συμβάσεις

Γωνίες πορείας, ανύψωσης και στροφής (Z-Y ′-X ″) για ένα αεροσκάφος που χρησιμοποιεί άξονες ENU (East-North-Up), τόσο επί του σκάφους όσο και για το σταθμό παρακολούθησης εδάφους. Το σταθερό σύστημα αναφοράς x-y-z αντιπροσωπεύει έναν τέτοιο σταθμό παρακολούθησης. Οι ενσωματωμένοι στο σκάφος άξονες Y και Z δεν εμφανίζονται. Το X εμφανίζεται σε πράσινο χρώμα. Αυτή η εικόνα δεν υπακούει στον κανόνα RHS : ο γ- άξονας πρέπει να αντιστραφεί για να σχηματίσει ένα RHS με ενδείξεις θετικών γωνιών.

Οι τρεις στοιχειώδεις περιστροφές μπορεί να γίνουν, είτε γύρω από τους άξονες του αρχικού συστήματος συντεταγμένων, ο οποίος παραμένει ακίνητο (εξωγενείς περιστροφές), είτε γύρω από τους άξονες του περιστρεφόμενου συστήματος συντεταγμένων, το οποίο αλλάζει τον προσανατολισμό του μετά από κάθε στοιχειώδη περιστροφή (ενδογενείς περιστροφές).

Υπάρχουν έξι δυνατότητες επιλογής των αξόνων περιστροφής για τις γωνίες Τέιτ–Μπράιαν. Οι έξι δυνατές ακολουθίες είναι:

• x - y ′-z ″ (ενδογενείς περιστροφές) ή z-y-x (εξωγενείς περιστροφές)
• y - z′ - x ″ (ενδογενείς περιστροφές) ή x-z-y (εξωγενείς περιστροφές)
• z - x' - y″ (ενδογενείς περιστροφές) ή y-x-z (εξωγενείς περιστροφές)
• x - z′ - y ″ (ενδογενείς περιστροφές) ή y-z-x (εξωγενείς περιστροφές)
• z - y ′ - x ″ (ενδογενείς περιστροφές) ή x - y - z (εξωγενείς περιστροφές): στην περίπτωση αυτή οι ενδογενείς περιστροφές είναι γνωστές ως: yaw, pitch και roll
• y - x ′ - z ″ (ενδογενείς περιστροφές) ή z - x - y (εξωγενείς περιστροφές)

Πρόσημα και περιοχές τιμών

Οι κύριοι άξονες ενός αεροσκάφους σύμφωνα με αεροπορικό πρότυπο DIN 9300. Σημειώστε ότι το σταθερό και κινητό σύστημα αναφοράς πρέπει να συμπίπτουν, όταν οι γωνίες μηδέν. Επομένως, αυτός ο κανονισμός θα επιβάλλει επίσης μια συμβατή σύμβαση αξόνων στο σύστημα αναφοράς

Η σύμβαση Τέιτ–Μπράιαν χρησιμοποιείται ευρέως στη μηχανική με διαφορετικούς σκοπούς. Στην πράξη υπάρχουν αρκετές συμβάσεις αξόνων για την επιλογή των κινητών και σταθερών αξόνων, και αυτές οι συμβάσεις καθορίζουν τα πρόσημα των γωνιών. Επομένως, τα πρόσημα πρέπει να μελετηθούν προσεκτικά σε κάθε περίπτωση.

Το εύρος τιμών για τις γωνίες ψ και φ καλύπτει 2π ακτίνια. Για τη γωνία θ το εύρος καλύπτει π ακτίνια.

Εναλλακτικά ονόματα

Οι παραπάνω γωνίες λαμβάνονται συνήθως μία στο εξωτερικό σύστημα αναφοράς (κατεύθυνση-heading, προσανατολισμός-bearing), μία στο εσωτερικό κινούμενο σύστημα αναφοράς (στροφή-bank ) και μία σε ένα μεσαίο σύστημα αναφοράς, που αντιπροσωπεύει μια ανύψωση ή κλίση ως προς το οριζόντιο επίπεδο, που ισοδυναμεί με τη γραμμή των κόμβων για το σκοπό αυτό.

Για ένα αεροσκάφος, μπορούν να ληφθούν με τρεις περιστροφές γύρω από τους κύριους άξονές του, εάν γίνουν με τη σωστή σειρά:

• Η Εκτροπή-Yaw θα δώσει την πορεία,
• Η Ανύψωση-pitch θα δώσει την ανύψωση και
• Η Στροφή-roll δίνει τη γωνία κλίσης.

Ως εκ τούτου, στην αεροδιαστημική ονομάζονται μερικές φορές yaw, pitch and roll. Σημειώστε ότι αυτό δεν θα λειτουργήσει, εάν οι περιστροφές εφαρμόζονται με οποιαδήποτε άλλη σειρά ή εάν οι άξονες του αεροπλάνου ξεκινούν σε οποιαδήποτε θέση μη ισοδύναμη με το παραπάνω πλαίσιο αναφοράς.

Οι γωνίες, Τέιτ–Μπράιαν σύμφωνα με τη σύμβαση z - y ′ - x ″ (ενδογενείς περιστροφές), είναι γνωστές ως ναυτικές γωνίες, επειδή μπορούν να χρησιμοποιηθούν για να περιγράψουν τον προσανατολισμό ενός πλοίου ή αεροσκάφους ή γωνίες Cardan από τον Ιταλό μαθηματικό και φυσικό Gerolamo Cardano, ο οποίος περιέγραψε για πρώτη φορά λεπτομερώς την ανάρτηση Cardan και την άρθρωση Cardan .

Γωνίες ενός δεδομένου συστήματος αναφοράς

Προβολές του διανύσματος Ζ

Προβολές του διανύσματος Υ

Ένα συνηθισμένο πρόβλημα είναι να βρείτε τις γωνίες Euler ενός δεδομένου συστήματος αναφοράς. Ο γρηγορότερος τρόπος για να τις βρείτε είναι να γράψετε τους τρία δεδομένα διανύσματα ως στήλες ενός πίνακα και να τον συγκρίνετε με την έκφραση του θεωρητικού πίνακα (βλ. παρακάτω τον πίνακα με τους πίνακες). Από εκεί μπορούν να υπολογιστούν και οι τρεις γωνίες Euler. Ωστόσο, μπορούμε να φτάσουμε στο ίδιο αποτέλεσμα αποφεύγοντας την άλγεβρα πινάκων, και χρησιμοποιώντας μόνο στοιχειώδη γεωμετρία. Εδώ παρουσιάζουμε τα αποτελέσματα για τις δύο πιο συχνά χρησιμοποιούμενες συμβάσεις:

• τη ZXZ για τις κύριες γωνίες Euler και
• τη ZYX για τις γωνίες Tait – Bryan.

Σημειώστε ότι μπορεί να ληφθεί οποιαδήποτε άλλη σύμβαση, αλλάζοντας μόνο το όνομα των αξόνων.

Κύριες γωνίες Euler

Θεωρούμε ένα περιστραμμένο σύστημα συντεταγμένων με διανύσματικές μονάδες (X,Y,Z) που δίνονται από τις συντεταγμένες τους στο κύριο σύστημα συντεταγμένων, όπως φαίνεται στο προηγούμενο σχήμα. Από εκεί φαίνεται ότι:

${\displaystyle \cos(\beta )=Z_{3}.}$

Και επειδή

${\displaystyle \sin ^{2}x=1-\cos ^{2}x,}$

για ${\displaystyle 0<x<\pi }$, οπότε sinx >0, έχουμε

${\displaystyle \sin(\beta )={\sqrt {1-Z_{3}^{2}}}.}$

Επειδή το ${\displaystyle Z_{2}}$ είναι η διπλή προβολή ενός μοναδιαίου διανύσματος,

${\displaystyle \cos(\alpha )\cdot \sin(\beta )=-Z_{2},}$

${\displaystyle \cos(\alpha )=-Z_{2}/{\sqrt {1-Z_{3}^{2}}}.}$

Υπάρχει μια παρόμοια κατασκευή για το ${\displaystyle Y_{3}}$, προβάλλοντας το πρώτα πάνω στο επίπεδο που ορίζεται από τον άξονα z και τη γραμμή των κόμβων. Καθώς η γωνία μεταξύ των επιπέδων είναι ${\displaystyle \pi /2-\beta }$ και ${\displaystyle \cos(\pi /2-\beta )=\sin(\beta )}$, αυτό οδηγεί σε:

${\displaystyle \sin(\beta )\cdot \cos(\gamma )=Y_{3},}$

${\displaystyle \cos(\gamma )=Y_{3}/{\sqrt {1-Z_{3}^{2}}},}$

και τέλος, χρησιμοποιώντας την αντίστροφη συνημιτονική συνάρτηση,

${\displaystyle \alpha =\arccos(-Z_{2}/{\sqrt {1-Z_{3}^{2}}}),}$

${\displaystyle \beta =\arccos(Z_{3}),}$

${\displaystyle \gamma =\arccos(Y_{3}/{\sqrt {1-Z_{3}^{2}}}).}$

Γωνίες Tait – Bryan

Θεωρούμε ένα σύστημα συντεταγμένων με μοναδιαία διανύσματα (X, Y, Z) που δίνονται από τις συντεταγμένες τους (παρατηρείστε ότι η γωνία θ είναι αρνητική),φαίνεται ότι:

${\displaystyle \sin(\theta )=-X_{3}}$

Όπως και πριν,

${\displaystyle \cos ^{2}x=1-\sin ^{2}x,}$

για ${\displaystyle -\pi /2<x<\pi /2}$ έχουμε

${\displaystyle \cos(\theta )={\sqrt {1-X_{3}^{2}}}.}$

κατά τρόπο ανάλογο με τον προηγούμενο:

${\displaystyle \sin(\psi )=X_{2}/{\sqrt {1-X_{3}^{2}}}.}$

${\displaystyle \sin(\phi )=Y_{3}/{\sqrt {1-X_{3}^{2}}}.}$

Ψάχνοντας για παρόμοιες εκφράσεις με τις προηγούμενες:

${\displaystyle \psi =\arcsin(X_{2}/{\sqrt {1-X_{3}^{2}}}),}$

${\displaystyle \theta =\arcsin(-X_{3}),}$

${\displaystyle \phi =\arcsin(Y_{3}/{\sqrt {1-X_{3}^{2}}}).}$

Τελευταίες παρατηρήσεις

Σημειώστε ότι οι αντίστροφες ημιτονικές και συνημιτονικές συναρτήσεις παρέχουν δύο πιθανές τιμές για το όρισμα. Σε αυτήν τη γεωμετρική περιγραφή ισχύει μόνο μία από τις λύσεις. Όταν οι γωνίες Euler ορίζονται ως μια σειρά περιστροφών, όλες οι λύσεις μπορεί να είναι έγκυρες, αλλά θα υπάρχει μόνο μία εντός ευρών τιμών των γωνιών. Αυτό συμβαίνει επειδή η ακολουθία περιστροφών για την επίτευξη του πλαισίου στόχου δεν είναι μοναδική, εάν δεν έχουν καθοριστεί προηγουμένως τα εύρη τιμών.^[2]

Για υπολογιστικούς σκοπούς, μπορεί να είναι χρήσιμο να απεικονίζονται οι γωνίες χρησιμοποιώντας τη συνάρτηση atan2(y, x) . Για παράδειγμα, στην περίπτωση κύριων γωνιών Euler:

${\displaystyle \alpha =\operatorname {atan2} (Z_{1},-Z_{2}),}$

${\displaystyle \gamma =\operatorname {atan2} (X_{3},Y_{3}).}$

Μετατροπή σε άλλες παραστάσεις για άλλους σκοπούς

Οι γωνίες Euler είναι ένας τρόπος αναπαράστασης των προσανατολισμών. Υπάρχουν και άλλοι, και είναι δυνατόν να αλλάξετε από και προς τις άλλες συμβάσεις. Απαιτούνται πάντα τρεις παράμετροι για την περιγραφή των προσανατολισμών σε έναν τρισδιάστατο ευκλείδειο χώρο . Μπορούν να δοθούν με διάφορους τρόπους, με τις γωνίες Euler να είναι μία από αυτές. δείτε γραφήματα στο SO (3) για άλλους.

Η αναπαράσταση προσανατολισμού που χρησιμοποιείται περισσότερο είναι οι πίνακες περιστροφής, η γωνία άξονα και τα τεταρτημόρια, επίσης γνωστά ως παράμετροι Euler-Rodrigues, οι οποίες παρέχουν έναν άλλο μηχανισμό για την αναπαράσταση τρισδιάστατων περιστροφών. Αυτό είναι ισοδύναμο με την περιγραφή της ειδικής ενιαίας ομάδας.

Η έκφραση των περιστροφών 3D σε unit quaternions αντί για πίνακες έχει ορισμένα πλεονεκτήματα:

• Οι συνεχόμενες περιστροφές είναι υπολογιστικά πιο γρήγορες και αριθμητικά πιο σταθερές.
• Η εξαγωγή της γωνίας και του άξονα περιστροφής είναι απλούστερη.
• Η παρεμβολή είναι πιο απλή. Δείτε για παράδειγμα slerp .
• Τα τεταρτημόρια δεν πάσχουν από κλειδώματα του Γυροσκοπίου (gimbal lock) όπως συμβαίνει με τιςγωνίες Euler.

Παρ' όλα αυτά, ο υπολογισμός του πίνακα περιστροφής είναι το πρώτο βήμα για τη λήψη των άλλων δύο αναπαραστάσεων.

Πίνακας περιστροφής

Όπως αναφέραμε παραπάνω οποιοσδήποτε προσανατολισμός μπορεί να επιτευχθεί συνθέτοντας τρεις στοιχειώδεις περιστροφές, ξεκινώντας από έναν γνωστό αρχικό προσανατολισμό. Ομοίως, κάθε πίνακας περιστροφής R μπορεί να αναπαρασταθεί ως γινόμενο τριών στοιχειωδών πινάκων περιστροφής. Για παράδειγμα:

${\displaystyle R=X(\alpha )Y(\beta )Z(\gamma )}$

είναι ένας πίνακας περιστροφής που μπορεί να χρησιμοποιηθεί για να αντιπροσωπεύει μια σύνθεση εξωγενών περιστροφών γύρω από τους άξονες z, y, x, (με αυτή τη σειρά), ή μια σύνθεση ενδογενών περιστροφών περί τους άξονες x - y ′ - z ″ (με αυτή τη σειρά). Ωστόσο, τόσο ο ορισμός των στοιχειωδών πινάκων περιστροφής X, Y, Z, όσο και η σειρά πολλαπλασιασμού τους, εξαρτώνται από τις επιλογές που έχει κάνει ο χρήστης σχετικά με τον ορισμό τόσο των πινάκων περιστροφής, όσο και των γωνιών Euler (βλέπε, για παράδειγμα, ασάφειες στον ορισμό των πινάκων περιστροφής ). Δυστυχώς, υιοθετούνται διαφορετικές συμβάσεις, από χρήστες σε διαφορετικά αντικείμενα. Ο παρακάτω πίνακας δημιουργήθηκε σύμφωνα με το ακόλουθο σύνολο συμβάσεων:

1. Κάθε πίνακας προορίζεται να λειτουργεί με προ-πολλαπλασιασμό διανυσμάτων στήλης ${\textstyle {\begin{bmatrix}x\\y\\z\end{bmatrix}}}$ (βλ. ασάφιες στον ορισμό των πινάκων περιστροφής )
2. Κάθε πίνακας προορίζεται να αντιπροσωπεύει μια ενεργή περιστροφή (οι συνιστώντες και συντιθέμενοι πίνακες υποτίθεται ότι δρουν στις συντεταγμένες των διανυσμάτων που ορίζονται στο αρχικό σταθερό πλαίσιο αναφοράς, και δίνουν σαν αποτέλεσμα τις συντεταγμένες του περιστραμένου διανύσματος πάλι στο αρχικό σύστημα αναφοράς).
3. Κάθε πίνακας προρίζεται να αντιπροσωπεύει, πρωτίστως, τη σύνθεση εξωγενών περιστροφών (που αντιστοιχεί στην κατασκευή του πίνακα R με τον πολλαπλασιασμό τριών στοιχειωδών πινάκων) και, δευτερευόντως, τη σύνθεση τριών μη στοιχειωδών πινάκων που αντιπροσωπεύουν γενικά ενδογενείς περιστροφές (γύρω από τους άξονες του περιστρεφόμενου συστήματος αναφοράς, με αντίστροφη σειρά).
4. Υιοθετούνται δεξιόστροφα συστήματα αναφοράς και χρησιμοποιείται ο κανόνας του δεξιού χεριού για τον προσδιορισμό του προσήμου των γωνιών α, β, γ .

Για λόγους απλότητας, ο ακόλουθος πίνακας του γινομένου των πινάκων χρησιμοποιεί την ακόλουθη ονοματολογία:

1. Τα 1, 2, 3 αντιπροσωπεύουν τις γωνίες α, β και γ αντίστοιχα, δηλαδή τις γωνίες που αντιστοιχούν στην πρώτη, δεύτερη και τρίτη στοιχειώδη περιστροφή αντίστοιχα.
2. Τα Χ, Υ, Ζ είναι οι πίνακες που αντιπροσωπεύουν τις στοιχειώδεις περιστροφές γύρω από τους άξονες x, y, z του σταθερού πλαισίου (π.χ., το X₁ αντιπροσωπεύει μια περιστροφή γύρω από τον άξονα x κατά γωνία α ).
3. Τα s και c αντιπροσωπεύουν ημίτονο και συνημίτονο (π.χ., το s₁ αντιπροσωπεύει το ημίτονο του α ).

Κύριες Γωνίες Euler	Gvn;iew Tait–Bryan
${\displaystyle X_{1}Z_{2}X_{3}={\begin{bmatrix}c_{2}&-c_{3}s_{2}&s_{2}s_{3}\\c_{1}s_{2}&c_{1}c_{2}c_{3}-s_{1}s_{3}&-c_{3}s_{1}-c_{1}c_{2}s_{3}\\s_{1}s_{2}&c_{1}s_{3}+c_{2}c_{3}s_{1}&c_{1}c_{3}-c_{2}s_{1}s_{3}\end{bmatrix}}}$	${\displaystyle X_{1}Z_{2}Y_{3}={\begin{bmatrix}c_{2}c_{3}&-s_{2}&c_{2}s_{3}\\s_{1}s_{3}+c_{1}c_{3}s_{2}&c_{1}c_{2}&c_{1}s_{2}s_{3}-c_{3}s_{1}\\c_{3}s_{1}s_{2}-c_{1}s_{3}&c_{2}s_{1}&c_{1}c_{3}+s_{1}s_{2}s_{3}\end{bmatrix}}}$
${\displaystyle X_{1}Y_{2}X_{3}={\begin{bmatrix}c_{2}&s_{2}s_{3}&c_{3}s_{2}\\s_{1}s_{2}&c_{1}c_{3}-c_{2}s_{1}s_{3}&-c_{1}s_{3}-c_{2}c_{3}s_{1}\\-c_{1}s_{2}&c_{3}s_{1}+c_{1}c_{2}s_{3}&c_{1}c_{2}c_{3}-s_{1}s_{3}\end{bmatrix}}}$	${\displaystyle X_{1}Y_{2}Z_{3}={\begin{bmatrix}c_{2}c_{3}&-c_{2}s_{3}&s_{2}\\c_{1}s_{3}+c_{3}s_{1}s_{2}&c_{1}c_{3}-s_{1}s_{2}s_{3}&-c_{2}s_{1}\\s_{1}s_{3}-c_{1}c_{3}s_{2}&c_{3}s_{1}+c_{1}s_{2}s_{3}&c_{1}c_{2}\end{bmatrix}}}$
${\displaystyle Y_{1}X_{2}Y_{3}={\begin{bmatrix}c_{1}c_{3}-c_{2}s_{1}s_{3}&s_{1}s_{2}&c_{1}s_{3}+c_{2}c_{3}s_{1}\\s_{2}s_{3}&c_{2}&-c_{3}s_{2}\\-c_{3}s_{1}-c_{1}c_{2}s_{3}&c_{1}s_{2}&c_{1}c_{2}c_{3}-s_{1}s_{3}\end{bmatrix}}}$	${\displaystyle Y_{1}X_{2}Z_{3}={\begin{bmatrix}c_{1}c_{3}+s_{1}s_{2}s_{3}&c_{3}s_{1}s_{2}-c_{1}s_{3}&c_{2}s_{1}\\c_{2}s_{3}&c_{2}c_{3}&-s_{2}\\c_{1}s_{2}s_{3}-c_{3}s_{1}&c_{1}c_{3}s_{2}+s_{1}s_{3}&c_{1}c_{2}\end{bmatrix}}}$
${\displaystyle Y_{1}Z_{2}Y_{3}={\begin{bmatrix}c_{1}c_{2}c_{3}-s_{1}s_{3}&-c_{1}s_{2}&c_{3}s_{1}+c_{1}c_{2}s_{3}\\c_{3}s_{2}&c_{2}&s_{2}s_{3}\\-c_{1}s_{3}-c_{2}c_{3}s_{1}&s_{1}s_{2}&c_{1}c_{3}-c_{2}s_{1}s_{3}\end{bmatrix}}}$	${\displaystyle Y_{1}Z_{2}X_{3}={\begin{bmatrix}c_{1}c_{2}&s_{1}s_{3}-c_{1}c_{3}s_{2}&c_{3}s_{1}+c_{1}s_{2}s_{3}\\s_{2}&c_{2}c_{3}&-c_{2}s_{3}\\-c_{2}s_{1}&c_{1}s_{3}+c_{3}s_{1}s_{2}&c_{1}c_{3}-s_{1}s_{2}s_{3}\end{bmatrix}}}$
${\displaystyle Z_{1}Y_{2}Z_{3}={\begin{bmatrix}c_{1}c_{2}c_{3}-s_{1}s_{3}&-c_{3}s_{1}-c_{1}c_{2}s_{3}&c_{1}s_{2}\\c_{1}s_{3}+c_{2}c_{3}s_{1}&c_{1}c_{3}-c_{2}s_{1}s_{3}&s_{1}s_{2}\\-c_{3}s_{2}&s_{2}s_{3}&c_{2}\end{bmatrix}}}$	${\displaystyle Z_{1}Y_{2}X_{3}={\begin{bmatrix}c_{1}c_{2}&c_{1}s_{2}s_{3}-c_{3}s_{1}&s_{1}s_{3}+c_{1}c_{3}s_{2}\\c_{2}s_{1}&c_{1}c_{3}+s_{1}s_{2}s_{3}&c_{3}s_{1}s_{2}-c_{1}s_{3}\\-s_{2}&c_{2}s_{3}&c_{2}c_{3}\end{bmatrix}}}$
${\displaystyle Z_{1}X_{2}Z_{3}={\begin{bmatrix}c_{1}c_{3}-c_{2}s_{1}s_{3}&-c_{1}s_{3}-c_{2}c_{3}s_{1}&s_{1}s_{2}\\c_{3}s_{1}+c_{1}c_{2}s_{3}&c_{1}c_{2}c_{3}-s_{1}s_{3}&-c_{1}s_{2}\\s_{2}s_{3}&c_{3}s_{2}&c_{2}\end{bmatrix}}}$	${\displaystyle Z_{1}X_{2}Y_{3}={\begin{bmatrix}c_{1}c_{3}-s_{1}s_{2}s_{3}&-c_{2}s_{1}&c_{1}s_{3}+c_{3}s_{1}s_{2}\\c_{3}s_{1}+c_{1}s_{2}s_{3}&c_{1}c_{2}&s_{1}s_{3}-c_{1}c_{3}s_{2}\\-c_{2}s_{3}&s_{2}&c_{2}c_{3}\end{bmatrix}}}$

These tabular results are available in numerous textbooks.^[3] For each column the last row constitutes the most commonly used convention.

To change the formulas for passive rotations (or find reverse active rotation), transpose the matrices (then each matrix transforms the initial coordinates of a vector remaining fixed to the coordinates of the same vector measured in the rotated reference system; same rotation axis, same angles, but now the coordinate system rotates, rather than the vector).

The following table contains formulas for angles α, β and γ from elements of a rotation matrix ${\displaystyle R}$.^[4]

Κύριες Γωνίες Euler		Γωνίε Tait–Bryan
${\displaystyle X_{1}Z_{2}X_{3}}$	${\displaystyle {\begin{aligned}\alpha &=\arctan \left({\frac {R_{31}}{R_{21}}}\right)\\\beta &=\arctan \left({\frac {\sqrt {1-R_{11}^{2}}}{R_{11}}}\right)\\\gamma &=\arctan \left({\frac {R_{13}}{-R_{12}}}\right)\end{aligned}}}$	${\displaystyle X_{1}Z_{2}Y_{3}}$	${\displaystyle {\begin{aligned}\alpha &=\arctan \left({\frac {R_{32}}{R_{22}}}\right)\\\beta &=\arctan \left({\frac {-R_{12}}{\sqrt {1-R_{12}^{2}}}}\right)\\\gamma &=\arctan \left({\frac {R_{13}}{R_{11}}}\right)\end{aligned}}}$
${\displaystyle X_{1}Y_{2}X_{3}}$	${\displaystyle {\begin{aligned}\alpha &=\arctan \left({\frac {R_{21}}{-R_{31}}}\right)\\\beta &=\arctan \left({\frac {\sqrt {1-R_{11}^{2}}}{R_{11}}}\right)\\\gamma &=\arctan \left({\frac {R_{12}}{R_{13}}}\right)\end{aligned}}}$	${\displaystyle X_{1}Y_{2}Z_{3}}$	${\displaystyle {\begin{aligned}\alpha &=\arctan \left({\frac {-R_{23}}{R_{33}}}\right)\\\beta &=\arctan \left({\frac {R_{13}}{\sqrt {1-R_{13}^{2}}}}\right)\\\gamma &=\arctan \left({\frac {-R_{12}}{R_{11}}}\right)\end{aligned}}}$
${\displaystyle Y_{1}X_{2}Y_{3}}$	${\displaystyle {\begin{aligned}\alpha &=\arctan \left({\frac {R_{12}}{R_{32}}}\right)\\\beta &=\arctan \left({\frac {\sqrt {1-R_{22}^{2}}}{R_{22}}}\right)\\\gamma &=\arctan \left({\frac {R_{21}}{-R_{23}}}\right)\end{aligned}}}$	${\displaystyle Y_{1}X_{2}Z_{3}}$	${\displaystyle {\begin{aligned}\alpha &=\arctan \left({\frac {R_{13}}{R_{33}}}\right)\\\beta &=\arctan \left({\frac {-R_{23}}{\sqrt {1-R_{23}^{2}}}}\right)\\\gamma &=\arctan \left({\frac {R_{21}}{R_{22}}}\right)\end{aligned}}}$
${\displaystyle Y_{1}Z_{2}Y_{3}}$	${\displaystyle {\begin{aligned}\alpha &=\arctan \left({\frac {R_{32}}{-R_{12}}}\right)\\\beta &=\arctan \left({\frac {\sqrt {1-R_{22}^{2}}}{R_{22}}}\right)\\\gamma &=\arctan \left({\frac {R_{23}}{R_{21}}}\right)\end{aligned}}}$	${\displaystyle Y_{1}Z_{2}X_{3}}$	${\displaystyle {\begin{aligned}\alpha &=\arctan \left({\frac {-R_{31}}{R_{11}}}\right)\\\beta &=\arctan \left({\frac {R_{21}}{\sqrt {1-R_{21}^{2}}}}\right)\\\gamma &=\arctan \left({\frac {-R_{23}}{R_{22}}}\right)\end{aligned}}}$
${\displaystyle Z_{1}Y_{2}Z_{3}}$	${\displaystyle {\begin{aligned}\alpha &=\arctan \left({\frac {R_{23}}{R_{13}}}\right)\\\beta &=\arctan \left({\frac {\sqrt {1-R_{33}^{2}}}{R_{33}}}\right)\\\gamma &=\arctan \left({\frac {R_{32}}{-R_{31}}}\right)\end{aligned}}}$	${\displaystyle Z_{1}Y_{2}X_{3}}$	${\displaystyle {\begin{aligned}\alpha &=\arctan \left({\frac {R_{21}}{R_{11}}}\right)\\\beta &=\arctan \left({\frac {-R_{31}}{\sqrt {1-R_{31}^{2}}}}\right)\\\gamma &=\arctan \left({\frac {R_{32}}{R_{33}}}\right)\end{aligned}}}$
${\displaystyle Z_{1}X_{2}Z_{3}}$	${\displaystyle {\begin{aligned}\alpha &=\arctan \left({\frac {R_{13}}{-R_{23}}}\right)\\\beta &=\arctan \left({\frac {\sqrt {1-R_{33}^{2}}}{R_{33}}}\right)\\\gamma &=\arctan \left({\frac {R_{31}}{R_{32}}}\right)\end{aligned}}}$	${\displaystyle Z_{1}X_{2}Y_{3}}$	${\displaystyle {\begin{aligned}\alpha &=\arctan \left({\frac {-R_{12}}{R_{22}}}\right)\\\beta &=\arctan \left({\frac {R_{32}}{\sqrt {1-R_{32}^{2}}}}\right)\\\gamma &=\arctan \left({\frac {-R_{31}}{R_{33}}}\right)\end{aligned}}}$

</br> Για να αλλάξετε τους τύπους για παθητικές περιστροφές (ή να βρείτε αντίστροφη ενεργή περιστροφή), αναστρέψτε τους πίνακες (τότε κάθε πίνακας μετατρέπει τις αρχικές συντεταγμένες ενός διανύσματος που παραμένουν σταθερές στις συντεταγμένες του ίδιου φορέα που μετριούνται στο περιστρεφόμενο σύστημα αναφοράς. Ίδιος άξονας περιστροφής, ίδιος γωνίες, αλλά τώρα το σύστημα συντεταγμένων περιστρέφεται, αντί του διανύσματος).

Ιδιότητες

Οι γωνίες Euler σχηματίζουν ένα γράφημα σε όλα τα SO (3), την ειδική ορθογώνια ομάδα περιστροφών σε 3D χώρο. Το γράφημα είναι ομαλό, εκτός από την ανωμαλία (singularity) σε αναπαράσταση πολικών συνταταγμένονων συντεταγμένου κατά μήκος του β = 0 . Δείτε διαγράμματα στο SO (3) για μια πιο ολοκληρωμένη ανάλυση.

Ο χώρος των περιστροφών ονομάζεται γενικά "Η Υπερσφαίρα των περιστροφών ", αν και αυτό είναι ένα ψευδές όνομα: η ομάδα Spin (3) είναι ισομετρική προς την υπερσφαίρα S ³, αλλά ο χώρος περιστροφής SO (3) είναι αντίθετα ισομετρικός στον πραγματικό προβολικό χώρο RP ³ που είναι ένας 2-fold quotient space της υπερσφαίρας. Αυτή η ασάφεια 2 προς 1 είναι η μαθηματική προέλευση του spin στη φυσική .

Μια παρόμοια αποσύνθεση τριών γωνιών ισχύει για το SU (2), την ειδική μονάδα περιστροφής στον Complex 2D χώρο, με τη διαφορά ότι το β κυμαίνεται από 0 έως 2π. Αυτές ονομάζονται επίσης γωνίες Euler.

Το μέτρο Haar για SO (3) σε γωνίες Euler δίνεται από την παραμετροποίηση γωνίας Hopf του SO (3), ${\displaystyle {\textrm {d}}V\propto \sin \alpha .{\textrm {d}}\alpha .{\textrm {d}}\beta .{\textrm {d}}\gamma }$,^[5] όπου ${\displaystyle (\alpha ,\beta )}$ παραμετροποιεί το ${\displaystyle S^{2}}$, το χώρος των αξόνων περιστροφής.

Για παράδειγμα, για να δημιουργήσετε ομοιόμορφα τυχαίους προσανατολισμούς, αφήστε τα α και γ να είναι ομοιόμορφα από 0 έως 2π, αφήστε το ζ να είναι ομοιόμορφο από − 1 έως 1 και αφήστε το β = arccos(z) .

Γεωμετρική άλγεβρα

Άλλες ιδιότητες των γωνιών Euler και γενικότερα των περιστροφών μπορούν να βρεθούν από τη Γεωμετρική άλγεβρα (GA). Η GA είναι μια αφαίρεση υψηλότερου επιπέδου, στην οποία τα τεταρτημόρια είναι πλήρης υποάλγεβρα. Το κύριο εργαλείο στη GA είναι ο ρότορας ${\displaystyle \mathbf {\mathbb {R} } =[\cos(\theta /2)-Iu\sin(\theta /2)]}$ όπου ${\displaystyle \mathbf {\theta } =}$ γωνία περιστροφής, ${\displaystyle \mathbf {(} u)=}$ άξονας περιστροφής (μοναδιαίο διάνυσμα) και ${\displaystyle \mathbf {(} I)=}$ ψευδοβαθμωτό (trivector στο ${\displaystyle \mathbb {R} ^{3}}$ )

Υψηλότερες διαστάσεις

Είναι δυνατόν να οριστούν παράμετροι ανάλογες με τις γωνίες Euler σε διαστάσεις μεγαλύτερες από τρεις.

Το πλήθος των βαθμών ελευθερίας ενός πίνακα περιστροφής, είναι πάντα μικρότερος από τη διάσταση του τετραγωνικού πίνακα. Δηλαδή, τα στοιχεία ενός πίνακας περιστροφής δεν είναι όλα εντελώς ανεξάρτητα. Για παράδειγμα, ο πίνακας περιστροφής στη διάσταση 2 έχει μόνο έναν βαθμό ελευθερίας, καθώς και τα τέσσερα στοιχεία του εξαρτώνται από μία μόνο γωνία περιστροφής. Ένας πίνακας περιστροφής με διάσταση 3 (ο οποίος έχει εννέα στοιχεία) έχει τρεις βαθμούς ελευθερίας, που αντιστοιχούν σε κάθε ανεξάρτητη περιστροφή, για παράδειγμα από τις τρεις γωνίες του Euler ή ένα τεταρτημόριο ενός (μονάδα) μεγέθους.

Στο SO (4) ο πίνακας περιστροφής ορίζεται από δύο τεταρτημόρια, και επομένως είναι 6-παραμετρικός (τρεις βαθμοί ελευθερίας για κάθε τεταρτημόριο). Οι πίνακες περιστροφής 4× 4 έχουν επομένως 6 ανεξάρτητες συνιστώσες από τις 16.

Οποιοδήποτε σύνολο 6 παραμέτρων που ορίζουν τον πίνακα περιστροφής θα μπορούσε να θεωρηθεί επέκταση των γωνιών Euler στην διάσταση 4.

Γενικά, το πλήθος των γωνιών euler στη διάσταση D είναι τετραγωνικός σε D. δεδομένου ότι οποιαδήποτε περιστροφή συνίσταται στην επιλογή δύο διαστάσεων για περιστροφή μεταξύ τους, ο συνολικός αριθμός περιστροφών που διατίθενται σε διάσταση ${\displaystyle D}$ είναι ${\displaystyle N_{rot}={\binom {D}{2}}=D(D-1)/2}$, για το οποίο ${\displaystyle D=2,3,4}$ αποδόσεις ${\displaystyle N_{rot}=1,3,6}$ .

Εφαρμογές

Ένα γυροσκόπιο διατηρεί τον άξονα περιστροφής του σταθερό. Επομένως, οι γωνίες που μετρώνται σε αυτό το σύστημα αναφοράς είναι ισοδύναμες με τις γωνίες που μετρώνται στο εργαστηριακό σύστημα αναφοράς.

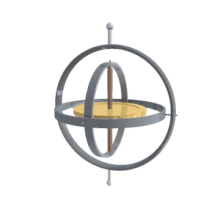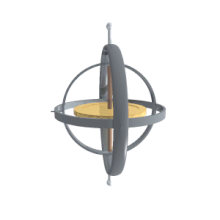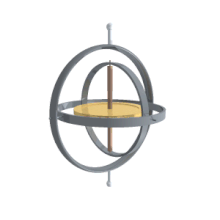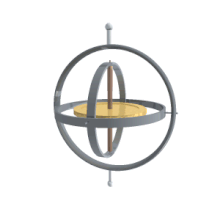
Οχήματα και κινούμενα πλαίσια

Το κύριο πλεονέκτημά τους έναντι άλλων περιγραφών προσανατολισμού, είναι ότι είναι οι γωνίες είναι άμεσα μετρήσιμες από ένα γυροσκόπιο (gimbal) στερεωμένο σε ένα όχημα. Καθώς τα γυροσκόπια διατηρούν τον άξονα περιστροφής σταθερό, οι γωνίες που μετρώνται σε ένα γυροσκόπιο, είναι ίσες με τις γωνίες που μετρώνται στο σύστημα αναφοράς του εργαστηρίου.

Ως εκ τούτου, τα γυροσκόπια χρησιμοποιούνται για να γνωρίζουμε τον πραγματικό προσανατολισμό των κινούμενων διαστημικών σκαφών, και οι γωνίες του Euler είναι άμεσα μετρήσιμες. Η εγγενής γωνία περιστροφής δεν μπορεί να διαβαστεί από ένα μόνο γυροσκόπιο , οπότε πρέπει να υπάρχουν περισσότερα από ένα γυροσκόπια σε ένα διαστημικό σκάφος. Κανονικά υπάρχουν τουλάχιστον τρία για πλεονασμό αλλά και για το γνωστό πρόβλημα της μηχανικής: του κλειδώματος του γυροσκοπίου ^[6]   .

Γενικά κατά τη μελέτη των στερεών σωμάτων, χρησιμοποιούμε δύο συστήματα συντεταγμένων. Το ένα είναι ένα αδρανειακό σύστημα αναφοράς, το οποίο το θεωρούμε ακίνητο και συμβολίζεται συνήθως με τα μικρά γράμματα με xyz, και το άλλο είναι στερεωμένο ακλόνητα πάνω στο στερεό σώμα, το σύστημα του σώματος, το οποίο και κινείται μαζί με αυτό και συμβολίζεται με τα κεφαλαία γράμματα XYZ .

Οι υπολογισμοί που αφορούν επιτάχυνση, γωνιακή επιτάχυνση, γωνιακή ταχύτητα,στροφορμή και κινητική ενέργεια είναι συχνά ευκολότεροι στο σύστημα αναφοράς του σώματος, επειδή τότε ο τανυστής της ροπής αδράνειας δεν αλλάζει με το χρόνο. Ο τανυστής αυτός είναι ένας πίνακας 3x3. Εάν κάποιος διαγωνιοποιήσει τον τανυστή αυτό (ο οποίος πριν από τη διαγωνοποίηση έχει εννέα στοιχεία, έξι από τα οποία είναι ανεξάρτητα), τότε έχει ένα σύστημα συντεταγμένων (που ονομάζονται οι κύριοι άξονες του τανυστή αδρανείας) όπου η ροπή αδράνειας έχει μόνο τρεις συνιστώσες.

Χρησιμοποιώντας τις γωνίες Euler, η γωνιακή ταχύτητα ενός στερεού σώματος παίρνει στο κινούμενο σύστημα αναφοράς, μία απλή μορφή. Επίσης, oι εξισώσεις Euler του στερεού σώματος είναι απλούστερες, επειδή στο κινούμενο σύστημα αναφοράς ο τανυστής αδράνειας είναι σταθερός.

Κρυσταλλογραφική υφή

Πολικές εικόνες (Pole figures) που δείχνουν την κρυσταλλογραφική υφή του γάμμα-TiAl σε ένα κράμα άλφα2-γ, όπως μετράται με ακτίνες Χ υψηλής ενέργειας.^[7]

Στην επιστήμη υλικών, η κρυσταλλογραφική υφή-texture (ή προτιμώμενος προσανατολισμός) μπορεί να περιγραφεί χρησιμοποιώντας τις γωνίες Euler. Στην ανάλυση υφής, οι γωνίες Euler παρέχουν μια μαθηματική απεικόνιση του προσανατολισμού των μεμονωμένων κρυσταλλιτών μέσα σε ένα πολυκρυσταλλικό υλικό, επιτρέποντας την ποσοτική περιγραφή του μακροσκοπικού υλικού.^[8] Ο πιο κοινός ορισμός των γωνιών οφείλεται στο Bunge και αντιστοιχεί στη σύμβαση ZXZ . Είναι σημαντικό, ωστόσο, να σημειωθεί ότι η εφαρμογή περιλαμβάνει γενικά μετασχηματισμούς άξονων των ποσοτήτων τανυστή, δηλαδή παθητικές περιστροφές. Έτσι, ο πίνακας που αντιστοιχεί στις γωνίες Bunge Euler, είναι ο ανάστροφος αυτού που φαίνεται στον παραπάνω πίνακα.^[9]

Άλλα

Βιομηχανικό ρομπότ που λειτουργεί σε χυτήριο

Οι γωνίες Euler, συνήθως στη σύμβαση Tait-Bryan, χρησιμοποιούνται επίσης στη ρομποτική όταν αναφερόμαστε στους βαθμούς ελευθερίας ενός βραχίονα . Χρησιμοποιούνται επίσης στον ηλεκτρονικό έλεγχο σταθερότητας με παρόμοιο τρόπο.

Τα συστήματα ελέγχου πυρός των κανονιών απαιτούν διορθώσεις των γωνιών προσανατολισμού τους (κατεύθυνση και ανύψωση) για να αντισταθμίσουν την κλίση του καταστρώματος (pitch and roll). Στα παραδοσιακά συστήματα, ένα σταθεροποιημένο γυροσκόπιο με κατακόρυφο άξονα περιστροφής διορθώνει την κλίση του καταστρώματος και σταθεροποιεί τα οπτικά σημεία και την κεραία ραντάρ. Ωστόσο, οι κάνες των κανονιών δείχνουν προς μια κατεύθυνση διαφορετική από την οπτική γωνία προς τον στόχο, για να αντιμετωπίσουν την κίνηση του στόχου και την πτώση του βλήματος, μεταξύ άλλων παραγόντων, και λόγω βαρύτητας. Η βάση του κανονιού περιστρέφεται με το επίπεδο του καταστρώματος και απαιτεί διόρθωση. Οι προσανατολισμοί των κανονιών περιλαμβάνουν γωνίες που υπολογίζονται από τα κατακόρυφα γυροσκοπικά δεδομένα, και αυτοί οι υπολογισμοί περιλαμβάνουν γωνίες Euler.

Οι γωνίες Euler χρησιμοποιούνται επίσης εκτενώς στην κβαντική μηχανική της γωνιακής ορμής. Στην κβαντική μηχανική, οι ρητές περιγραφές των αναπαραστάσεων του SO (3) είναι πολύ σημαντικές για τους υπολογισμούς και σχεδόν όλη η εργασία έχει γίνει με γωνίες Euler. Στην πρώιμη ιστορία της κβαντικής μηχανικής, όταν οι φυσικοί και οι χημικοί είχαν μια έντονα αρνητική αντίδραση στις αφηρημένες θεωρητικές μεθόδους της ομάδας (που ονομάζονται Gruppenpest ), η εξάρτηση από τις γωνίες του Euler ήταν επίσης απαραίτητη για τη βασική θεωρητική εργασία.

Πολλές φορητές υπολογιστικές συσκευές περιέχουν επιταχυνσιόμετρα που μπορούν να προσδιορίσουν τις γωνίες Euler αυτών των συσκευών, σε σχέση με το διάνυσμα της βαρύτητας της γης. Αυτά χρησιμοποιούνται σε εφαρμογές όπως παιχνίδια, προσομοιώσεις αλφαδιών φυσαλίδων και καλειδοσκόπια .  

Δείτε επίσης

• Προβολή 3D
• Αναπαράσταση γωνίας άξονα
• Μετατροπή μεταξύ τεταρτημορίων και γωνιών Euler
• Διαδοχικές περιστροφές Davenport
• Θεώρημα περιστροφής του Euler
• Κλείδωμα Gimbal
• Τεταρτημόρια
• Τεταρτημόρια και χωρική περιστροφή
• Φορμαλισμοί περιστροφής σε τρεις διαστάσεις
• Σφαιρικό σύστημα συντεταγμένων

Παραπομπές

1. Novi Commentarii academiae scientiarum Petropolitanae 20, 1776, pp. 189–207 (E478) PDF
2. «Gregory G. Slabaugh, Computing Euler angles from a rotation matrix» (PDF). Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 11 Ιανουαρίου 2020. Ανακτήθηκε στις 29 Δεκεμβρίου 2022. 
3. E.g. Appendix I (p. 483) of: Roithmayr, Carlos M.; Hodges, Dewey H. (2016), Dynamics: Theory and Application of Kane's Method (1st έκδοση), Cambridge University Press, ISBN 978-1107005693 
4. Henderson, D. M. (1977-06-09) (στα αγγλικά). Euler angles, quaternions, and transformation matrices for space shuttle analysis, σελ. 12–24. https://ntrs.nasa.gov/citations/19770019231. 
5. Section 8 - Derivation of Hopf parametrisation : Generating Uniform Incremental Grids on SO(3) Using the Hopf Fibration  .
6. The relation between the Euler angles and the Cardan suspension is explained in chap. 11.7 of the following textbook: U. Krey, A. Owen, Basic Theoretical Physics – A Concise Overview, New York, London, Berlin, Heidelberg, Springer (2007) .
7. «High energy X-rays: A tool for advanced bulk investigations in materials science and physics». Textures Microstruct. 35 (3/4): 219–52. 2003. doi:10.1080/07303300310001634952. 
8. Kocks, U.F.; Tomé, C.N.; Wenk, H.-R. (2000), Texture and Anisotropy: Preferred Orientations in Polycrystals and their effect on Materials Properties, Cambridge, ISBN 978-0-521-79420-6 
9. Bunge, H. (1993), Texture Analysis in Materials Science: Mathematical Methods, Cuvillier Verlag