Εισαγωγή στη γενική σχετικότητα
| Αυτό το λήμμα χρειάζεται επιμέλεια ώστε να ανταποκρίνεται σε υψηλότερες προδιαγραφές ορθογραφικής και συντακτικής ποιότητας ή μορφοποίησης. Αίτιο: τυπογραφικά λάθη, επιμέλεια μετάφρασης για συντακτικά-μεταφραστικά λάθη, ομοιομορφία ονομάτων Για περαιτέρω βοήθεια, δείτε τα λήμματα πώς να επεξεργαστείτε μια σελίδα και τον οδηγό μορφοποίησης λημμάτων. |
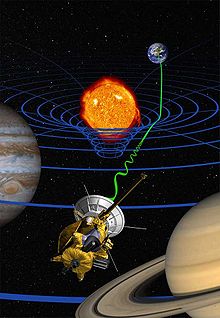
Η γενική σχετικότητα είναι μια θεωρία της βαρύτητας που αναπτύχθηκε από τον Άλμπερτ Αϊνστάιν (Albert Einstein) μεταξύ 1907 και 1915. Σύμφωνα με τη γενική σχετικότητα, η παρατηρούμενη βαρυτική επίδραση μεταξύ μαζών είναι αποτέλεσμα της στρέβλωσης του χωροχρόνου που τις περιβάλλει.
Μέχρι τις αρχές του 20ού αιώνα, ο νόμος της παγκόσμιας έλξης του Νεύτωνα είχε γίνει δεκτός για περισσότερα από διακόσια χρόνια ως μια έγκυρη περιγραφή της βαρυτικής δύναμης μεταξύ μαζών. Στο μοντέλο του Νεύτωνα, η βαρύτητα είναι το αποτέλεσμα μιας ελκτικής δύναμης μεταξύ αντικειμένων με μεγάλη μάζα. Παρά το γεγονός ότι ακόμα και ο Νεύτωνας ήταν προβληματισμένος από την άγνωστη φύση αυτής της δύναμης[1], το βασικό πλαίσιο ήταν εξαιρετικά επιτυχές στην περιγραφή της κίνησης.
Τα πειράματα και οι παρατηρήσεις δείχνουν ότι η περιγραφή του Αϊνστάιν για τη βαρύτητα, εξηγεί διάφορα αποτελέσματα τα οποία είναι ανεξήγητα από το νόμο του Νεύτωνα, όπως λεπτομερειακές ανωμαλίες στις τροχιές του Ερμή και άλλων πλανητών. Η γενική σχετικότητα προβλέπει επίσης καινοτόμες συνέπειες της βαρύτητας, όπως τα κύματα βαρύτητας, βαρυτικό εστιασμό και την επίδραση της βαρύτητας στο χρόνο, γνωστή ως βαρυτική διαστολή του χρόνου. Πολλές από αυτές τις προβλέψεις έχουν επιβεβαιωθεί πειραματικά, ενώ άλλοι αποτελούν αντικείμενο της εν εξελίξει έρευνας. Για παράδειγμα, αν και υπάρχουν έμμεσες ενδείξεις για τα βαρυτικά κύματα, άμεση απόδειξη της ύπαρξής τους εξακολουθούν να αναζητούνται από αρκετές ομάδες επιστημόνων σε πειράματα όπως τα προγράμματα LIGO και GEO 600.
Η γενική σχετικότητα έχει εξελιχθεί σε ένα βασικό εργαλείο της σύγχρονης αστροφυσικής. Παρέχει τα θεμέλια για την τρέχουσα κατανόηση των μαύρων τρυπών, περιοχές του διαστήματος όπου η βαρυτική επίδραση είναι τόσο ισχυρή ώστε ούτε το φως δεν μπορεί να ξεφύγει. Η ισχυρή βαρύτητά τους πιστεύεται ότι είναι υπεύθυνη για την έντονη ακτινοβολία που εκπέμπεται από ορισμένους τύπους των αστρονομικών αντικειμένων (όπως ενεργούς γαλαξιακούς πυρήνες ή μικροκβάζαρς (microquasars)). Η γενική σχετικότητα είναι επίσης μέρος του πλαισίου του καθιερωμένου μοντέλου της Μεγάλη Έκρηξης (Big Bang) της κοσμολογίας.
Παρά το γεγονός ότι η γενική σχετικότητα δεν είναι η μόνη σχετικιστική θεωρία της βαρύτητας, είναι η απλούστερη τέτοια θεωρία που είναι συνεπής με τα πειραματικά δεδομένα. Παρ 'όλα αυτά, μια σειρά από αναπάντητα ερωτήματα παραμένουν, το πιο θεμελιώδες από τα οποία είναι το πώς η γενική σχετικότητα μπορεί να συμβιβαστεί με τους νόμους της κβαντικής φυσικής για να παράγουν μία πλήρη και αυτο-συνεπή θεωρία κβαντικής βαρύτητας.
Από την ειδική στη γενική σχετικότητα
[Επεξεργασία | επεξεργασία κώδικα]Τον Σεπτέμβριο του 1905, ο Άλμπερτ Αϊνστάιν δημοσίευσε τη θεωρία της ειδικής σχετικότητας, η οποία συμβιβάζει τους νόμους της κίνησης του Νεύτωνα με την ηλεκτροδυναμική (αλληλεπίδραση μεταξύ των αντικειμένων με ηλεκτρικό φορτίο). Η Ειδική Σχετικότητα εισήγαγε ένα νέο πλαίσιο για το σύνολο της φυσικής προτείνοντας νέες έννοιες του χώρου και του χρόνου. Μερικές αποδεκτές θεωρίες της φυσικής εκείνη την εποχή, ήταν ασυμβίβαστες με το πλαίσιο. Ένα βασικό παράδειγμα ήταν η θεωρία της βαρύτητας του Νεύτωνα, που περιγράφει την αμοιβαία έλξη που υπόκεινται τα σώματα εξαιτίας της μάζας τους.
Αρκετοί φυσικοί, συμπεριλαμβανομένου του Αϊνστάιν, έψαξε για μια θεωρία που θα συμβιβάσει το νόμο της βαρύτητας του Νεύτωνα και την ειδική θεωρία της σχετικότητας. Μόνο η θεωρία του Αϊνστάιν αποδείχθηκε να είναι συνεπής με τα πειράματα και παρατηρήσεις. Για να κατανοήσει κάποιος τις βασικές ιδέες της θεωρίας, είναι διδακτικό να ακολουθήσει το σκεπτικό του Αϊνστάιν μεταξύ 1907 και 1915, από το απλό του πείραμα σκέψης που συμπεριλαμβάνει ένα παρατηρητή σε ελεύθερη πτώση, μέχρι την πλήρη γεωμετρική θεωρία της βαρύτητας.[2]
Αρχή της ισοδυναμίας
[Επεξεργασία | επεξεργασία κώδικα]Το πείραμα σκέψης ήταν το εξής: ένα άτομο που βρίσκεται σε ελεύθερη πτώση μέσα σε ένα ασανσέρ βιώνει την έλλειψη βάρους, ενώ τα αντικείμενα είτε επιπλέουν ακίνητα ή παρασύρονται με σταθερή σχετική ταχύτητα. Δεδομένου ότι τα πάντα στο ασανσέρ πέφτουν μαζί, καμία βαρυτική επίδραση δε μπορεί να παρατηρηθεί. Με τον τρόπο αυτό, οι εμπειρίες που βιώνει ένας παρατηρητής σε ελεύθερη πτώση δεν έχουν διαφορά από εκείνες ενός παρατηρητή στο βαθύ διάστημα, μακριά από οποιαδήποτε σημαντική πηγή βαρύτητας. Οι εν λόγω παρατηρητές είναι οι "προνομιούχοι" (αδρανειακοί) παρατηρητές που ο Αϊνστάιν περιέγραψε στη θεωρία του για την ειδική σχετικότητα: παρατηρητές για τους οποίους το φως ταξιδεύει σε ευθείες γραμμές με σταθερή ταχύτητα.[3]
Ο Αϊνστάιν υπέθεσε ότι οι παρόμοιες εμπειρίες των παρατηρητών χωρίς βάρος και των αδρανειακών παρατηρητών στην ειδική σχετικότητα αντιπροσώπευε μια θεμελιώδη ιδιότητα της βαρύτητας, την οποία έκανε τον ακρογωνιαίο λίθο της θεωρίας του της γενικής σχετικότητας και επισημοποιήθηκε στην αρχή της ισοδυναμίας του. Σε γενικές γραμμές, η αρχή αναφέρει ότι ένα άτομο σε ελεύθερη πτώση μέσα σε ασανσέρ δεν μπορεί διακρίνει αν όντως είναι σε ελεύθερη πτώση ή όχι. Κάθε πείραμα σε ένα τέτοιο περιβάλλον με ελεύθερη πτώση έχει τα ίδια αποτελέσματα που θα είχε ένας παρατηρητής σε ηρεμία ή κινούμενος με σταθερή ταχύτητα στο βαθύ διάστημα, μακριά από όλες τις πηγές βαρύτητας.[4]
Βαρύτητα και επιτάχυνση
[Επεξεργασία | επεξεργασία κώδικα]
Οι περισσότερες επιδράσεις της βαρύτητας εξαφανίζονται σε ελεύθερη πτώση, αλλά τα αποτελέσματα που φαίνονται τα ίδια με εκείνα της βαρύτητας μπορεί να παράγονται από ένα επιταχυνόμενο πλαίσιο αναφοράς. Ένας παρατηρητής σε ένα κλειστό δωμάτιο δεν μπορεί να πει ποια από τα παρακάτω είναι αληθές:
- Αντικείμενα πέφτουν στο πάτωμα επειδή το δωμάτιο είναι ακίνητο πάνω στην επιφάνεια της Γης και τα αντικείμενα έλκονται προς τα κάτω από τη βαρύτητα.
- Αντικείμενα πέφτουν στο πάτωμα επειδή το δωμάτιο είναι πάνω σε ένα πύραυλο στο διάστημα, το οποίο επιταχύνεται κατά 9,81 m/s2 και είναι μακριά από κάθε πηγή βαρύτητας. Τα αντικείμενα έλκονται προς το πάτωμα από την ίδια "αδρανειακή δύναμη" που πιέζει τον οδηγό ενός αυτοκινήτου που επιταχύνεται στην πλάτη του καθίσματος του.
Αντίθετα, οι τυχόν επιπτώσεις που παρατηρήθηκαν σε ένα επιταχυνόμενο σύστημα αναφοράς πρέπει επίσης να παρατηρηθούν σε ένα βαρυτικό πεδίο αντίστοιχης δύναμης. Αυτή η αρχή επέτρεψε τον Αϊνστάιν να προβλέψει αρκετά νέα αποτελέσματα της βαρύτητας το 1907, όπως εξηγείται και στην επόμενη ενότητα.
Ένας παρατηρητής σε ένα επιταχυνόμενο σύστημα αναφοράς πρέπει να εισάγει αυτό που οι φυσικοί αποκαλούν φανταστικές δυνάμεις (ή ψευδοδυνάμεις) για να τεκμηριώσει την επιτάχυνση στην οποία υπόκειται και τα αντικείμενα γύρω του. Ένα παράδειγμα που έχει ήδη αναφερθεί, είναι η δύναμη που πιέζει τον οδηγό ενός επιταχυνόμενου αυτοκινήτου στο κάθισμά του. Άλλο ένα είναι η δύναμη που μπορεί να νιώσει κάποιος με το μάζεμα και τέντωμα των χεριών εάν προσπαθήσει να γυρίσει γύρω γύρω σαν σβούρα. Η κύρια διορατική εικόνα του Αϊνστάιν ήταν ότι η σταθερή και γνωστή έλξη του βαρυτικού πεδίου της Γης, είναι ουσιαστικά το ίδιο με αυτές τις φανταστικές δυνάμεις.[5] Το φαινομενικό μέγεθος των φανταστικών δυνάμεων εμφανίζεται πάντα να είναι ανάλογο προς τη μάζα του κάθε αντικειμένου στο οποίο ενεργούν. Για παράδειγμα, το κάθισμα του οδηγού ασκεί ακριβώς τόση δύναμη ώστε να επιταχυνθεί ο οδηγός με τον ίδιο ρυθμό όπως και το αυτοκίνητο. Κατ 'αναλογία, ο Αϊνστάιν πρότεινε ότι ένα αντικείμενο σε ένα βαρυτικό πεδίο θα πρέπει να αισθάνεται μια βαρυτική δύναμη ανάλογη με τη μάζα του, όπως ενσωματώνεται στο νόμο της βαρύτητας του Νεύτωνα.[6]
Φυσικές συνέπειες
[Επεξεργασία | επεξεργασία κώδικα]
Το 1907, ο Αϊνστάιν ήταν ακόμα οκτώ χρόνια μακριά από την ολοκλήρωση της γενικής θεωρίας της σχετικότητας. Παρ 'όλα αυτά, ήταν σε θέση να κάνει μια σειρά από καινοτόμες, ελέγξιμες προβλέψεις που βασίστηκαν στο σημείο εκκίνησης του για την ανάπτυξη της νέας θεωρίας του: Την αρχή της ισοδυναμίας.[7]
Το πρώτο νέο αποτέλεσμα είναι η βαρυτική μετατόπιση συχνότητας του φωτός. Θεωρήστε δύο παρατηρητές πάνω σε έναν επιταχυνόμενο διαστημόπλοιο. Σε ένα τέτοιο όχημα, υπάρχει μια φυσική έννοια του "πάνω" και του "κάτω": Η κατεύθυνση στην οποία το όχημα επιταχύνει είναι "πάνω" και μη προσκολλημένα αντικείμενα επιταχύνονται προς την αντίθετη κατεύθυνση, πέφτοντας "προς τα κάτω". Ας υποθέσουμε ότι ένας από τους παρατηρητές είναι "πιο ψηλά" από τον άλλο. Όταν ο κατώτερος παρατηρητής στέλνει ένα φωτεινό σήμα στον υψηλότερο παρατηρητή, η επιτάχυνση αναγκάζει το φως να μετατοπιστεί προς το ερυθρό (κόκκινο), όπως μπορεί να υπολογιστεί από την ειδική σχετικότητα. Ο δεύτερος παρατηρητής θα μετρήσει μια χαμηλότερη συχνότητα για το φως από την πρώτο. Αντίθετα, το φως που αποστέλλεται από τον πάνω παρατηρητή στον κάτω είναι μετατοπισμένο προς το κυανό (μπλε), δηλαδή, μετατοπίζεται προς υψηλότερες συχνότητες.[8] Ο Αϊνστάιν υποστήριξε ότι αυτές οι μετατοπίσεις συχνότητας θα πρέπει επίσης να παρατηρηθούν σε ένα βαρυτικό πεδίο. Αυτό απεικονίζεται στο σχήμα στα αριστερά, το οποίο δείχνει ένα κύμα φωτός που σταδιακά μετατοπίζεται προς το ερυθρό όπως αυτό προχωράει προς τα πάνω αντίθετα της επιτάχυνσης της βαρύτητας. Αυτό το αποτέλεσμα έχει επιβεβαιωθεί πειραματικά, όπως περιγράφεται παρακάτω.
Αυτή η βαρυτική μετατόπιση συχνότητας αντιστοιχεί σε μια βαρυτική διαστολή του χρόνου: εφόσον ο "ανώτερος" παρατηρητής μετρά στο ίδιο κύμα φωτός μία χαμηλότερη συχνότητα από τον "κατώτερο" παρατηρητή, ο χρόνος πρέπει να διέρχεται κυλάει ταχύτερα για τον υψηλότερο παρατηρητή. Έτσι, ο χρόνος κυλάει πιο αργά για τους παρατηρητές οι οποίοι βρίσκονται χαμηλότερα σε ένα βαρυτικό πεδίο.
Είναι σημαντικό να τονιστεί ότι για κάθε παρατηρητή, δεν υπάρχουν παρατηρήσιμες μεταβολές της ροής του χρόνου για γεγονότα ή διαδικασίες που βρίσκονται σε κατάσταση ηρεμίας στο δικό του σύστημα αναφοράς. Π.χ. αυγά που βράζουν πέντε λεπτά όπως χρονομετρούνται από το ρολόι του κάθε παρατηρητή έχουν την ίδια συνοχή. Όταν ένας χρόνος περνάει σε κάθε ρολόι, ο κάθε παρατηρητής μεγαλώνει κατά την ίδια ποσότητα. Εν ολίγοις, κάθε ρολόι είναι σε τέλεια συμφωνία με όλες τις διαδικασίες που συμβαίνουν στο άμεσο περιβάλλον του. Μόνο όταν τα ρολόγια συγκριθούν μεταξύ διαφορετικών παρατηρητών, μπορεί κανείς να παρατηρήσει ότι ο χρόνος κυλάει πιο αργά για τον κατώτερο παρατηρητή από ότι για τον ανώτερο.[9] Αυτό το αποτέλεσμα είναι πολύ μικρό, αλλά έχει επίσης επιβεβαιωθεί πειραματικά σε πολλαπλά πειράματα, όπως περιγράφεται παρακάτω.
Κατά παρόμοιο τρόπο, ο Αϊνστάιν προέβλεψε την βαρυτική εκτροπή του φωτός: μέσα σε ένα βαρυτικό πεδίο, το φως εκτρέπεται ακολουθώντας το καμπύλο τμήμα του χωροχρόνου. Ποσοτικά, τα αποτελέσματά του διέφεραν από τη θεωρία κατά δύο φορές. Η σωστή προέλευση της θεωρίας απαιτεί μια πιο ολοκληρωμένη διατύπωση της θεωρίας της γενικής σχετικότητας, όχι μόνο της αρχής της ισοδυναμίας.[10]
Παλιρροιακά φαινόμενα
[Επεξεργασία | επεξεργασία κώδικα]
Η ισοδυναμία μεταξύ βαρυτικών και αδρανειακών φαινομένων δεν αποτελεί μια πλήρη θεωρία της βαρύτητας. Όταν πρόκειται για την εξήγηση της βαρύτητας κοντά στην δική μας θέση στην επιφάνεια της Γης, προσφέρει μια κατάλληλη εξήγηση, σημειώνοντας ότι το σύστημα αναφοράς μας δεν είναι σε ελεύθερη πτώση έτσι ώστε να αναμένονται φανταστικές δυνάμεις. Αλλά ένα πλαίσιο αναφοράς που είναι σε ελεύθερη πτώση στη μία πλευρά της Γης, δεν μπορεί να εξηγήσει γιατί οι άνθρωποι στην αντίθετη πλευρά της Γης αισθάνονται μια βαρυτική έλξη στην αντίθετη κατεύθυνση.
Μια πιο βασική εκδήλωση του ίδιου αποτελέσματος περιλαμβάνει δύο σώματα που πέφτουν δίπλα-δίπλα προς τη Γη. Σε ένα σύστημα αναφοράς που είναι σε ελεύθερη πτώση παραπλεύρως με αυτά τα σώματα, φαίνονται να αιωρούνται χωρίς βάρος, αλλά δεν είναι ακριβώς έτσι. Αυτά τα σώματα φορείς δεν πέφτουν ακριβώς στην ίδια κατεύθυνση, αλλά προς ένα μοναδικό σημείο στο χώρο: το κέντρο της βαρύτητας της Γης. Συνεπώς, υπάρχει μία συνιστώσα της κίνησης του κάθε σώματος προς το άλλο (βλέπε σχήμα. Σε ένα μικρό περιβάλλον, όπως σε ένα ανελκυστήρα που είναι σε ελεύθερη πτώση, αυτή η σχετική επιτάχυνση είναι αμελητέα, ενώ για skydivers (αλεξιπτωτιστές) στις αντίθετες πλευρές της Γης, η επίδραση είναι μεγάλη. Αυτές οι διαφορές στις δυνάμεις είναι επίσης υπεύθυνες για τις παλίρροιες στους ωκεανούς της Γης, έτσι ο όρος "παλιρροιακή επίδραση" χρησιμοποιείται για το φαινόμενο αυτό.
Η ισοδυναμία μεταξύ αδράνειας και βαρύτητας δεν μπορεί να εξηγήσει παλιρροιακά φαινόμενα.[11] Δεν μπορεί να εξηγήσει διακυμάνσεις στο βαρυτικό πεδίο. Για αυτό το λόγο, είναι απαραίτητη μια θεωρία η οποία περιγράφει τον τρόπο με τον οποίο η ύλη (όπως η μεγάλη μάζα της Γης) επηρεάζει την αδρανειακό περιβάλλον γύρω από αυτή.
Από την επιτάχυνση στη γεωμετρία
[Επεξεργασία | επεξεργασία κώδικα]Στη διερεύνηση της ισοδυναμίας της βαρύτητας και της επιτάχυνσης καθώς επίσης και στο το ρόλο των παλιρροιακών δυνάμεων, ο Αϊνστάιν ανακάλυψε πολλές αναλογίες με τη γεωμετρία επιφανειών. Ένα παράδειγμα είναι η μετάβαση από ένα αδρανειακό σύστημα αναφοράς (στο οποίο ελεύθερα σωματίδια κινούνται κατά μήκος ευθειών σε σταθερές ταχύτητες) σε ένα περιστρεφόμενο σύστημα αναφοράς (στο οποίο επιπλέον όροι που αντιστοιχούν σε εικονικές δυνάμεις πρέπει να εισαχθούν προκειμένου να εξηγήθεί η κίνηση των σωματιδίων). Αυτό είναι ανάλογο με τη μετάβαση από ένα καρτεσιανό σύστημα συντεταγμένων (στο οποίο οι γραμμές συντεταγμένων είναι ευθείες γραμμές) σε ένα καμπυλόγραμμο σύστημα συντεταγμένων (όπου δεν είναι απαραίτητο οι γραμμές συντεταγμένων να είναι ευθείες).
Μια βαθύτερη αναλογία συσχετίζει τις παλιρροιακές δυνάμεις με μια ιδιότητα των επιφανειών που ονομάζεται καμπυλότητα. Για βαρυτικά πεδία, η απουσία ή η παρουσία παλιρροιακών δυνάμεων καθορίζει αν η επιρροή της βαρύτητας μπορεί να εξαλειφθεί με την επιλογή ενός συστήματος αναφοράς σε ελεύθερη πτώση. Ομοίως, η απουσία ή παρουσία καμπυλότητας καθορίζει αν μια επιφάνεια είναι ισοδύναμη με ένα επίπεδο. Το καλοκαίρι του 1912 εμπνευσμένος από αυτές τις αναλογίες, ο Αϊνστάιν έψαξε για μια γεωμετρική διαμόρφωση της βαρύτητας.[12]
Τα στοιχειώδη αντικείμενα της γεωμετρίας - σημεία, γραμμές, τρίγωνα - κλασικά ορίζονται στο τρισδιάστατο χώρο ή σε δισδιάστατες επιφάνειες. Το 1907, ο μαθηματικός Hermann Minkowski (ο οποίος ήταν πρώην καθηγητής μαθηματικών του Αϊνστάιν στο Ελβετικό Ομοσπονδιακό Πολυτεχνείο) εισήγαγε μια γεωμετρική διαμόρφωση της ειδικής σχετικότητας του Αϊνστάιν στο οποίο η γεωμετρία περιλαμβάνει όχι μόνο χώρο, αλλά και χρόνο. Ο βασική ιδεά αυτής της νέας γεωμετρίας είναι ο τετραδιάστατος χωροχρόνος. Οι τροχιές των κινούμενων σωμάτων είναι καμπύλες στο χωροχρόνο. Οι τροχιές των κινούμενων σωμάτων που κινούνται με σταθερή ταχύτητα χωρίς να αλλάξουν κατεύθυνση αντιστοιχούν σε ευθείες γραμμές.[13]
Για επιφάνειες, η γενίκευση από τη γεωμετρία του επιπέδου - μια επίπεδη επιφάνεια - σε εκείνη μιας γενικής κυρτής επιφάνειας είχε περιγραφεί στις αρχές του 19ου αιώνα από τον Καρλ Φρίντριχ Γκάους (Carl Friedrich Gauss). Η περιγραφή αυτή είχε με τη σειρά της γενικευτεί σε χώρους υψηλότερων διαστάσεων σε ένα μαθηματικό φορμαλισμό που εισήγαγε ο Μπέρναρντ Ρίμαν (Bernhard Riemann) στη δεκαετία του 1850. Με τη βοήθεια της Γεωμετρίας του Riemann, ο Αϊνστάιν διατύπωσε μια γεωμετρική περιγραφή της βαρύτητας στην οποία ο χωροχρόνος Μινκόφσκι (Minkowski) έχει αντικατασταθεί από τον στρεβλωμένο και καμπύλο χωροχρόνο, ακριβώς όπως και οι καμπύλες επιφάνειες αποτελούν μια γενίκευση των απλών επίπεδων επιφάνειες.[14]
Αφού είχε συνειδητοποιήσει την ισχύ αυτής της γεωμετρικής αναλογίας,ο Αιστάιν χρειάστηκε τρία επιπλέον χρόνια για να βρει τον ακρογωνιαίο λίθο που έλειπε από τη θεωρία του: οι εξισώσεις που περιγράφουν πώς η ύλη επηρεάζει την καμπυλότητα του χωροχρόνου. Έχοντας διατυπώσει αυτές που είναι τώρα γνωστές ως εξισώσεις του Αϊνστάιν (ή ακριβέστερα, εξισώσεις πεδίου βαρύτητας), παρουσίασε τη νέα του θεωρία της βαρύτητας σε αρκετές συνεδρίες της Πρωσικής Ακαδημίας Επιστημών στα τέλη του 1915.[15]
Γεωμετρία και βαρύτητα
[Επεξεργασία | επεξεργασία κώδικα]Παραφράζοντας τον John Wheeler, η γεωμετρική θεωρία της βαρύτητας του Αϊνστάιν μπορεί να συνοψιστεί ως εξής: ο χωροχρόνος λέει στην ύλη πώς να κινηθεί και η ύλη λέει στο χωροχρόνο πώς να καμπυλωθεί.[16] Η ερμηνεία αυτής της φράσης συζητείται στις ακόλουθες τρεις ενότητες, οι οποίες διερευνούν την κίνηση των αποκαλούμενων σωματιδίων δοκιμής, εξετάζουν ποιες ιδιότητες της ύλης χρησιμεύουν ως πηγή για τη βαρύτητα και τέλος, να εισαγάγουν τις εξισώσεις του Αϊνστάιν που συσχετίζουν αυτές τις ιδιότητες ύλης με την καμπυλότητα του χωροχρόνου.
Ανίχνευση του Βαρυτικού πεδίου
[Επεξεργασία | επεξεργασία κώδικα]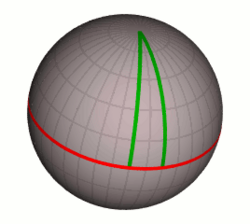
Για να χαρτογραφηθεί η βαρυτική επίδραση ενός σώματος, είναι χρήσιμο να σκεφτούμε τι οι φυσικοί αποκαλούν σωματίδια δοκιμής (ή εξέτασης): σωματίδια που επηρεάζονται από τη βαρύτητα, αλλά είναι τόσο μικρά και ελαφρά που μπορούμε να παραμελήσουμε τη δική τους βαρυτική επίδραση. Σε απουσία της βαρύτητας και άλλων εξωτερικών δυνάμεων, ένα σωματίδιο δοκιμής κινείται κατά μήκος μιας ευθείας γραμμής με σταθερή ταχύτητα. Στη γλώσσα του χωροχρόνου, αυτό είναι ισοδύναμο με το να πούμε ότι αυτά τα σωματίδια κινούνται κατά μήκος ευθείων καθολικών γραμμών στον χωροχρόνο. Η καθολική γραμμή ενός αντικειμένου είναι η μοναδική διαδρομή του καθώς αυτό ταξιδεύει μέσα στον 4-διάστατο χωροχρόνο (χωροχρόνος Minkowski). Με την παρουσία της βαρύτητας, ο χωρόχρονος είναι μη Ευκλείδιος ή καμπυλωμένος και σε καμπύλο χωροχρόνο οι ευθείες καθολικές γραμμές ίσως να μην υπάρχουν. Αντίθετα, τα σωματίδια δοκιμής κινούνται κατά μήκος των γραμμών που ονομάζονται γεωδαισιακές (geodesics), οι οποίες είναι οι πιο ευθείες κατά το δυνατόν.
Μια απλή αναλογία είναι η εξής: Στη Γεωδαισία, την επιστήμη της μέτρησης του μεγέθους και το σχήματος της Γης, μία γεωδαισιακή καμπύλη είναι η συντομότερη διαδρομή μεταξύ δύο σημείων στην επιφάνεια της Γης. Προσεγγιστικά, μια τέτοια διαδρομή είναι ένα τμήμα ενός μεγάλου κύκλου, όπως μια γραμμή γεωγραφικού μήκους (μεσημβρινός) ή ο ισημερινός. Αυτές οι διαδρομές σίγουρα δεν είναι ευθείες, απλά επειδή πρέπει να ακολουθούν την καμπυλότητα της επιφάνειας της Γης. Αλλά είναι τόσο ευθείες όσο είναι δυνατόν, εφόσον υπόκεινται σε αυτόν τον περιορισμό.
Οι ιδιότητες των γεωδαισιακών διαφέρουν από εκείνες των ευθειών γραμμών. Για παράδειγμα, σε ένα επίπεδο οι παράλληλες γραμμές ποτέ δεν τέμνονται, αλλά αυτό δεν ισχύει για γεωδαισιακές στην επιφάνεια της Γης: για παράδειγμα, οι γραμμές του γεωγραφικού μήκους είναι παράλληλες στον ισημερινό, αλλά τέμνονται στους πόλους. Ανάλογα, οι καθολικές γραμμές των σωματιδίων δοκιμής σε ελεύθερη πτώση είναι γεωδαισιακές χωροχρόνου, οι πιο ευθείες κατά το δυνατόν γραμμές στο χωροχρόνο. Αλλά ακόμα υπάρχουν κρίσιμες διαφορές μεταξύ αυτών και των πραγματικά ευθειών γραμμών που μπορούν να εντοπιστούν στο χωροχρόνο μηδενικής βαρύτητας της ειδικής σχετικότητας. Στην ειδική σχετικότητα, παράλληλες γεωδαισιακές παραμένουν παράλληλες. Σε ένα βαρυτικό πεδίο με παλιρροιακές επιδράσεις, γενικά, αυτό δε θα είναι η περίπτωση. Αν για παράδειγμα δύο σώματα είναι αρχικά σε μεταξύ τους, αλλά στη συνέχεια ρίχνονται στο πεδίο βαρύτητας της Γης, θα κινηθούν το ένα προς το άλλο καθώς πέφτουν προς το κέντρο της Γης.[17]
Σε σύγκριση με τους πλανήτες και άλλα αστρονομικά σώματα, τα αντικείμενα της καθημερινής ζωής (άνθρωποι, αυτοκίνητα, σπίτια, ακόμη και τα βουνά) έχουν μικρή μάζα. Όσον αφορά αυτά τα αντικείμενα, οι νόμοι που διέπουν τη συμπεριφορά των σωματιδίων δοκιμής είναι επαρκείς για να περιγράψουν το τι συμβαίνει. Συγκεκριμένα, προκειμένου να εκτραπεί ένα σωματίδιο δοκιμής από τη γεωδαιτική πορεία του, μία εξωτερική δύναμη πρέπει να ασκηθεί. Ένα άτομο που κάθεται σε μια καρέκλα τείνει να ακολουθήσει μια γεωδαισιακή, που είναι η ελεύθερη πτώση προς το κέντρο της Γης. Αλλά η καρέκλα εφαρμόζει μια εξωτερική δύναμη προς τα πάνω εμποδίζοντας το άτομο να πέσει. Με αυτόν τον τρόπο, η γενική σχετικότητα εξηγεί την καθημερινή εμπειρία της βαρύτητας πάνω στην επιφάνεια της Γης όχι σαν προς τα κάτω έλξη μιας βαρυτικής δύναμης, αλλά σαν προς τα πάνω ώθηση των εξωτερικών δυνάμεων. Αυτές οι δυνάμεις εκτρέπουν όλα τα σώματα που εδράζονται στην επιφάνεια της Γης από τις γεωδαιτικές που διαφορετικά θα ακολουθούσαν.[18] Για υλικά αντικείμενα των οποίων η δικιά τους βαρυτική επίδραση δεν μπορεί να αγνοηθεί, οι νόμοι της κίνησης είναι κάπως πιο περίπλοκοι από ότι για τα σωματίδια δοκιμών, αν και παραμένει αληθές ότι ο χωροχρόνος λέει στην ύλη πώς να κινηθεί.[19]
Πηγές της βαρύτητας
[Επεξεργασία | επεξεργασία κώδικα]Στην περιγραφή της βαρύτητας από το Νεύτωνα, η βαρυτική δύναμη προκαλείται από την ύλη. Ακριβέστερα, προκαλείται από μια ειδική ιδιότητα των υλικών αντικειμένων: τη μάζα τους. Στη θεωρία του Αϊνστάιν και στις σχετικές θεωρίες της βαρύτητας, η καμπυλότητα σε κάθε σημείο του χωροχρόνου προκαλείται επίσης από οποιαδήποτε ύλη είναι παρούσα. Εδώ επίσης, η μάζα είναι μια ιδιότητα κλειδί για τον προσδιορισμό της βαρυτικής επίδρασης της ύλης. Αλλά σε μια σχετικιστική θεωρία της βαρύτητας, η μάζα δεν μπορεί να είναι η μόνη πηγή της βαρύτητας. Η σχετικότητα συνδέει τη μάζα με την ενέργεια και την ενέργεια με την ορμή.
Η ισοδυναμία μεταξύ μάζας και ενέργειας, όπως αυτή εκφράζεται από τον τύπο E = mc2, είναι η πιο διάσημη συνέπεια της ειδικής σχετικότητας. Στην σχετικότητα, η μάζα και η ενέργεια είναι δύο διαφορετικοί τρόποι περιγραφής μιας φυσικής ποσότητας (υλοενέργεια). Εάν ένα φυσικό σύστημα έχει ενέργεια, έχει επίσης και την αντίστοιχη μάζα, και αντιστρόφως. Ειδικότερα, όλες οι ιδιότητες ενός σώματος που σχετίζονται με την ενέργεια, όπως η θερμοκρασία ή η ενέργεια σύνδεσης συστημάτων όπως πυρήνες ή μόρια, συμβάλλουν στην μάζα αυτού του σώματος και συνεπώς ενεργούν ως πηγές βαρύτητας.[20]
Στην ειδική σχετικότητα, η ενέργεια συνδέεται στενά με την ορμή. Ακριβώς όπως ο χώρος και ο χρόνος σε αυτή τη θεωρία, είναι διαφορετικές πτυχές μιας πιο ολοκληρωμένης οντότητας με την ονομασία χωροχρόνος, η ενέργεια και η ορμή είναι απλώς διαφορετικές πτυχές μιας ενοποιημένης τετραδιάστατης ποσότητας που οι φυσικοί αποκαλούν τετρα-ορμή. Συνεπώς, εάν η ενέργεια είναι μία πηγή βαρύτητας, τότε και η ορμή πρέπει να είναι επίσης μια πηγή. Το ίδιο ισχύει και για ποσότητες που έχουν άμεση σχέση με την ενέργεια και την ορμή, δηλαδή την εσωτερική πίεση και την ένταση. Συνολικά, στη γενική σχετικότητα ως πηγές βαρύτητας λειτουργούν η μάζα, η ενέργεια, η ορμή, η πίεση και η ένταση. Αυτές ευθύνονται για το γεγονός ότι η ύλη λέει στο χωροχρόνο πώς να καμπυλωθεί. Στη μαθηματική διατύπωση της θεωρίας, όλες αυτές οι ποσότητες δεν είναι παρά πτυχές μιας γενικότερης φυσικής ποσότητας που ονομάζεται τανυστής ενέργειας-ορμής.[21]
Εξισώσεις του Αϊνστάιν
[Επεξεργασία | επεξεργασία κώδικα]
Οι εξισώσεις του Αϊνστάινείναι το επίκεντρο της γενικής σχετικότητας. Παρέχουν μια ακριβή διατύπωση της σχέσης μεταξύ της γεωμετρίας του χωροχρόνου και των ιδιοτήτων της ύλης, χρησιμοποιώντας τη γλώσσα των μαθηματικών. Πιο συγκεκριμένα, αυτές διαμορφώνονται με τη χρήση των εννοιών της γεωμετρίας Riemann, στην οποία οι γεωμετρικές ιδιότητες ενός χώρου (ή χωροχρόνου) περιγράφονται από μία ποσότητα που ονομάζεται μετρική . Η μετρική κωδικοποιεί τις πληροφορίες που απαιτούνται για τον υπολογισμό των βασικών γεωμετρικών εννοιών της απόστασης και της γωνίας σε ένα καμπύλο χώρο (ή χωροχρόνο).
Μια σφαιρική επιφάνεια όπως αυτή της Γης παρέχει ένα απλό παράδειγμα. Η θέση οποιουδήποτε σημείου πάνω στην επιφάνεια μπορεί να περιγραφεί με δύο συντεταγμένες: το γεωγραφικό πλάτος και το γεωγραφικό μήκος. Σε αντίθεση με τις καρτεσιανές συντεταγμένες του επιπέδου, οι διαφορές συντεταγμένων δεν είναι οι ίδιες με τις αποστάσεις στην επιφάνεια, όπως φαίνεται στο σχήμα δεξιά: για κάποιον στον ισημερινό που κινείται 30 μοίρες γεωγραφικού μήκους δυτικά (μωβ γραμμή) αντιστοιχεί σε μια απόσταση περίπου 3.300 χιλιόμετρα (2.100 mi). Από την άλλη πλευρά, κάποιος σε γεωγραφικό πλάτος 55 μοιρών, που κινείται 30 μοίρες γεωγραφικού μήκους δυτικά (μπλε γραμμή) καλύπτει μια απόσταση περίπου 1.900 χιλιόμετρα (1.200 mi). Οι συντεταγμένες συνεπώς δεν παρέχουν αρκετές πληροφορίες για να περιγράψουν τη γεωμετρία μιας σφαιρικής επιφάνειας, πόσο μάλλον τη γεωμετρία ενός πιο περίπλοκου χώρου ή χωροχρόνου. Οι εν λόγω πληροφορίες είναι ακριβώς αυτό που κωδικοποιείται στη μετρική, η οποία είναι μια συνάρτηση που ορίζεται σε κάθε σημείο της επιφάνειας (ή χώρου, ή χωροχρόνου) και συσχετίζει διαφορές συντεταγμένων με διαφορές στην απόσταση. Όλες οι άλλες ποσότητες που παρουσιάζουν ενδιαφέρον στη γεωμετρία, όπως το μήκος μιας οποιασδήποτε δεδομένης καμπύλης ή η γωνία στην οποία δύο καμπύλες συναντιούνται, μπορεί να υπολογιστεί από αυτή τη μετρική συνάρτηση.[22]
Η μετρική συνάρτηση και ο ρυθμός μεταβολής της από σημείο σε σημείο μπορεί να χρησιμοποιηθεί για να ορίσει μια γεωμετρική ποσότητα που ονομάζεται τανυστής καμπυλότητας Riemann, ο οποίος περιγράφει πώς ακριβώς ο χώρος (ή χωροχρόνος) είναι καμπυλωμένος σε κάθε σημείο. Στη γενική σχετικότητα, η μετρική και ο τανυστής καμπυλότητας Riemann είναι ποσότητες που ορίζονται σε κάθε σημείο στον χωροχρόνο. Όπως έχει ήδη αναφερθεί, το περιεχόμενο ύλης του χωροχρόνου ορίζει μια άλλη ποσότητα, τον τανυστή ενέργειας-ορμής T, και την αρχή ότι "ο χωροχρόνος λέει στην ύλη πώς να κινηθεί, και η ύλη λέει στον χωροχρόνο πώς να καμπυλωθεί" εννοώντας ότι οι ποσότητες αυτές πρέπει να συνδέονται η μία με την άλλη.Ο Einstein διατύπωσε αυτή τη σχέση με χρήση του τανυστή καμπυλότητας Riemann και της μετρικής για να ορίσει μια άλλη γεωμετρική ποσότητα G, που σήμερα ονομάζεται τανυστής Einstein, η οποία περιγράφει μερικές πτυχές του τρόπου με τον οποίο ο χωροχρόνος καμπυλώνεται. Η εξίσωση του Einstein δηλώνει στη συνέχεια ότι:
δηλαδή, μέχρι ένα σταθερό πολλαπλάσιο, η ποσότητα G (η οποία μετρά καμπυλότητα) εξισώνεται με την ποσότητα Τ (η οποία μετρά περιεχόμενο ύλης). Οι σταθερές που περιλαμβάνονται σε αυτήν την εξίσωση, αντικατοπτρίζουν τις διαφορετικές θεωρίες που χρησιμοποιήθηκαν για τη δημιουργία της: ο αριθμός π είναι μία από τις βασικές σταθερές της γεωμετρίας, G είναι η βαρυτική σταθερά που είναι ήδη παρούσα στη νευτώνεια βαρύτητα, και c είναι η ταχύτητα του φωτός, η σταθερά-κλειδί στην ειδική σχετικότητα.
Η εξίσωση αυτή συχνά αναφέρεται στον πληθυντικό, σαν εξισώσεις Einstein, εφόσον οι ποσότητες G και Τ προσδιορίζονται η καθεμιά με διάφορες συναρτήσεις των συντεταγμένων του χωροχρόνου, και οι εξισώσεις εξισώνουν κάθε μία από αυτές τις συναρτήσεις-συνιστώσες.[23] Κάθε λύση αυτών των εξισώσεων περιγράφουν μια συγκεκριμένη γεωμετρία τουχωροχρόνου. Για παράδειγμα, η λύση Schwarzschild περιγράφει τη γεωμετρία γύρω από μια σφαιρική, μη περιστρεφόμενη μάζα, όπως ένα άστρο ή μια μαύρη τρύπα, ενώ η λύση Kerr περιγράφει μια περιστρεφόμενη μαύρη τρύπα. Επιπλέον, άλλες λύσεις μπορεί να περιγράφουν ένα κύμα βαρύτητας ή στην περίπτωση της λύσης Friedmann-Lemaître-Robertson-Walker, ένα διαστελλόμενο σύμπαν. Η απλούστερη λύση είναι ο μη καμπυλωμένος χωροχρόνος Minkowski, ο χωροχρόνος που περιγράφεται από την ειδική σχετικότητα.[24]
Οι πειραματικές δοκιμές
[Επεξεργασία | επεξεργασία κώδικα]Καμία επιστημονική θεωρία δεν είναι αποδεδειγμένα σωστή. Κάθε μία είναι ένα μοντέλο που πρέπει να ελέγχεται πειραματικά. Ο νόμος της βαρύτητας του Νεύτωναέγινε αποδεκτός διότι εξηγούσε την κίνηση των πλανητών και των δορυφόρων του ηλιακού συστήματος με μεγάλη ακρίβεια. Καθώς η ακρίβεια των πειραματικών μετρήσεων βελτιώθηκε σταδιακά, παρατηρήθηκαν ορισμένες αποκλίσεις από τις προβλέψεις του Νεύτωνα, οι οποίες δικαιολογούνται στη γενική θεωρία της σχετικότητας. Ομοίως, οι προβλέψεις της γενικής σχετικότητας πρέπει επίσης να ελέγχονται πειραματικά, έτσι και ο ίδιος ο Αϊνστάιν επινόησε τρεις δοκιμές γνωστές πλέον ως τα κλασικά τεστ της θεωρίας:

- Η Νευτώνεια βαρύτητα προβλέπει ότι η τροχιά στην οποία περιστρέφεται ένας μεμονωμένος πλανήτης γύρω από έναν εντελώς σφαιρικό αστέρα θα πρέπει να είναι μια έλλειψη . Η θεωρία του Αϊνστάιν προβλέπει μια πιο περίπλοκη καμπύλη: ο πλανήτης συμπεριφέρεται σαν να κινούνταν έλλειπτικά, αλλά την ίδια στιγμή η έλλειψη σαν σύνολο περιστρέφεται αργά γύρω από το άστρο. Στο διάγραμμα στα δεξιά, η έλλειψη που προβλέπεται από τη νευτώνεια βαρύτητα εμφανίζεται με κόκκινο χρώμα, ενώ μέρος της τροχιάς που προβλέπεται από τον Einstein σε μπλε χρώμα. Για ένα πλανήτη που είναι σε τροχιά γύρω από τον Ήλιο, αυτή η απόκλιση από τις τροχιές του Νεύτωνα είναι γνωστή ως η (ανώμαλη) μετακίνηση του περιηλίου. Η πρώτη μέτρηση αυτής της επίδρασης, για τον πλανήτη Ερμή, χρονολογείται το 1859. Τα πιο ακριβή αποτελέσματα για τον Ερμή και άλλους πλανήτες, μέχρι σήμερα βασίζονται στις μετρήσεις που πραγματοποιήθηκαν μεταξύ 1966 και 1990,όπου χρησιμοποιήθηκαν ραδιοτηλεσκόπια.[25] Η γενική σχετικότητα προβλέπει τη σωστή μετακίνηση του περιηλίου για όλους τους πλανήτες όπου αυτό μπορεί να μετρηθεί με ακρίβεια ( Ερμής , Αφροδίτη και Γη ).
- Σύμφωνα με τη γενική σχετικότητα, το φως δεν ταξιδεύει σε ευθείες γραμμές όταν διαδίδεται σε ένα βαρυτικό πεδίο. Αντιθέτως, εκτρέπεται με την παρουσία σωμάτων με μάζα. Συγκεκριμένα, το αστρικό φώς (από ένα μακρινό άστρο) εκτρέπεται καθώς περνά κοντά από τον Ήλιο, κάτι που οδηγεί σε φαινόμενες μετατοπίσεις μέχρι 1,75 arcsec (δευτερόλεπτα τόξου) στις θέσεις των άστρων στον ουρανό (ένα δευτερόλεπτο τόξου μοίρας είναι ίσο με το 1/3600 της μίας μοίρας. Στο πλαίσιο της νευτώνειας βαρύτητας, ένα πειραματικό επιχείρημα μπορεί να γίνει που οδηγεί σε εκτροπή του φωτός κατά το μισό αυτής της ποσότητας. Οι διαφορετικές προβλέψεις μπορούν να ελεγχθούν παρατηρώντας τα άστρα που βρίσκονται κοντά στον ήλιο κατά τη διάρκεια μιας ηλιακής έκλειψης. Με τον τρόπο αυτό, μια βρετανική αποστολή στη Δυτική Αφρική το 1919, που διευθύνθηκε από τον Arthur Eddington, επιβεβαίωσε ότι η πρόβλεψη του Αϊνστάιν ήταν σωστή και οι Νευτώνειες προβλέψεις λάθος, μέσω της παρατήρησης της ηλιακής έκλειψης το Μάιο του 1919. Τα αποτελέσματα του Eddington δεν ήταν πολύ ακριβή. Μεταγενέστερες παρατηρήσεις της εκτροπής του φωτός των μακρινών κβάζαρ από τον Ήλιο, που χρησιμοποιούν εξαιρετικά ακριβείς τεχνικές της ραδιοαστρονομίας, επιβεβαίωσαν τα αποτελέσματα του Eddington με σημαντικά μεγαλύτερη ακρίβεια (οι πρώτες τέτοιες μετρήσεις χρονολογούνται το 1967, η πιο πρόσφατη ολοκληρωμένη ανάλυση το 2004).[26]
- Η βαρυτική μετατόπιση προς το ερυθρό (gravitational redshift) μετρήθηκε για πρώτη φορά σε ένα εργαστήριο το 1959 από τους Poundκαι Rebka. Έχει επίσης παρατηρηθεί σε αστροφυσικές μετρήσεις, ειδικά στο φως που διαφεύγει από το λευκό νάνο Sirius Β. Η σχετική επίδραση της βαρυτικής διαστολής του χρόνου έχει μετρηθεί με τη μεταφορά ατομικών ρολογιών σε υψόμετρα μεταξύ δεκάδων και δεκάδων χιλιάδων χιλιομέτρων (πρώτα από τους Hafele και Keating το 1971 και τα ακριβέστερα μέχρι στιγμής από το δορυφόρο Gravity Probe A που ξεκίνησε το 1976).[27]
Από τις δοκιμές αυτές, μόνο η ανοδική πορεία του περιηλίου του Ερμή ήταν γνωστή πριν από την τελική δημοσίευση του Αϊνστάιν για τη γενική σχετικότητα το 1916. Η επακόλουθη πειραματική επιβεβαίωση άλλων προβλέψεών του, ειδικά οι πρώτες μετρήσεις της παραμόρφωσης του φωτός από τον Ήλιο το 1919, εκτόξευσε τον Einstein στο διεθνές επιστημονικό στερέωμα.[28] Αυτές οι τρεις πειραματικές δοκιμές δικαιολογούν την επικράτηση της γενικής σχετικότητας σε σχέση με τη θεωρία του Νεύτωνα και παρεμπιπτόντως, σε σχέση με αρκετές εναλλακτικές θεωρίες της γενικής σχετικότητας που είχαν προταθεί.
Περαιτέρω δοκιμές της γενικής σχετικότητας περιλαμβάνουν μετρήσεις ακριβείας του φαινομένου Shapiro ή αλλιώς τη βαρυτική χρονική καθυστέρηση του φωτός, και πιο πρόσφατα το 2002 από το διαστημικό σκάφος Cassini. Ένα σύνολο δοκιμών επικεντρώνεται στα αποτελέσματα που προβλέπoνται από τη γενική σχετικότητα για τη συμπεριφορά των γυροσκοπίων που ταξιδεύουν μέσα στο χώρο. Ένα από αυτά τα αποτελέσματα, η γεωδαιτική μετάπτωση, έχει δοκιμαστεί με το πείραμα Lunar Laser Ranging (μετρήσεις υψηλής ακρίβειας της τροχιάς της Σελήνης). Ένα άλλο, το οποίο σχετίζεται με περιστρεφόμενες μάζες, ονομάζεται frame-dragging (ή βαρυτομαγνητισμός ή φαινόμενο Λένζε-Tίρρινγκ). Τα αποτελέσματα γεωδαιτικής μετάπτωσης και frame dragging ελέγχθηκαν και τα δύο από το πείραμα με το δορυφόρο Gravity Probe B που ξεκίνησε το 2004, επιβεβαιώνοντας τη σχετικότητα με ακρίβεια 0,5% και 15% αντίστοιχα, το Δεκέμβριο του 2008.[29]
Σε κοσμικές κλίμακες, η βαρύτητα μέσα στο ηλιακό σύστημα είναι αδύναμη. Δεδομένου ότι οι διαφορές ανάμεσα στις προβλέψεις του Αϊνστάιν και τις θεωρίες του Νεύτωνα είναι πιο έντονες όταν η βαρύτητα είναι ισχυρή, οι φυσικοί έχουν εδώ και πολύ καιρό ενδιαφερθεί για τη δοκιμή διάφορων σχετικιστικών αποτελεσμάτων σε ένα περιβάλλον με συγκριτικά ισχυρά βαρυτικά πεδία. Αυτό έχει καταστεί δυνατό χάρη στις ακριβείς παρατηρήσεις ακριβείας των δυαδικών πάλσαρ (binary pulasrs). Σε ένα τέτοιο σύστημα αστέρων, δύο εξαιρετικά συμπαγείς αστέρες νετρονίων είναι σε τροχιά ο ένας γύρω από τον άλλον. Τουλάχιστον ένας από αυτούς είναι πάλσαρ - ένα αστρονομικό αντικείμενο που εκπέμπει μια στενή δέσμη ραδιοκυμάτων. Αυτές οι ακτίνες προσπίππτουν στη Γη σε πολύ τακτά χρονικά διαστήματα, παρόμοια με τον τρόπο που η περιστρεφόμενη ακτίνα ενός φάρου εμφανίζεται σε ένα παρατηρητή ο οποίος βλέπει την αναλαμπή του φάρου, και μπορεί να παρατηρηθεί ως μία πολύ τακτική σειρά παλμών. Η γενική σχετικότητα προβλέπει συγκεκριμένες αποκλίσεις από την τακτικότητα αυτών των ραδιοφωνικών παλμών. Για παράδειγμα, όταν κατά καιρούς τα ραδιοκύματα περνούν κοντά στο άλλο άστρο νετρονίων, αυτά πρέπει να εκτρέπονται από το βαρυτικό πεδίο του άστρου. Τα παρατηρούμενα μοτίβα παλμών είναι εντυπωσιακά κοντά σε αυτά που προβλέπονται από τη γενική σχετικότητα.[30]
Ένα συγκεκριμένο σύνολο παρατηρήσεων σχετίζονται με κατ 'εξοχήν χρήσιμες πρακτικές εφαρμογές, συγκεκριμένα στα δορυφορικά συστήματα πλοήγησης όπως το GPS(Παγκόσμιο Σύστημα Εντοπισμού Θέσης) που χρησιμοποιούνται τόσο για την ακριβή εντοπισμό θέσης όσο και για την ακριβή χρονομέτρηση. Τα συστήματα αυτά βασίζονται σε δύο ομάδες ατομικών ρολογιών: ρολόγια πάνω σε δορυφόρους σε τροχιά γύρω από τη Γη και ρολόγια αναφοράς τοποθετημένα στην επιφάνεια της Γης. Η γενική σχετικότητα προβλέπει ότι αυτά τα δύο σετ ρολογιών θα πρέπει να χτυπούν σε ελαφρώς διαφορετικούς ρυθμούς, λόγω των διαφορετικών κινήσεών τους (ένα αποτέλεσμα που έχει ήδη προβλεφθεί από την ειδική σχετικότητα) και των διαφορετικών θέσεων τους μέσα στο βαρυτικό πεδίο της Γης. Προκειμένου να εξασφαλιστεί η ακρίβεια του συστήματος, τα δορυφορικά ρολόγια είτε επιβραδύνονται από ένα σχετικιστικό συντελεστή, ή ο ίδιος συντελεστής γίνεται μέρος του αλγορίθμου αξιολόγησης. Με τη σειρά τους, οι δοκιμές της ακρίβειας του συστήματος (ειδικά οι πολύ ενδελεχείς μετρήσεις που αποτελούν μέρος του ορισμού του Συγχρονισμένου Παγκόσμιου Χρόνου UTC ) είναι η απόδειξη για την εγκυρότητα των σχετικιστικών προβλέψεων.[31]
Αρκετές άλλες δοκιμές έχουν εξετάσει την εγκυρότητα των διάφορων εκδοχών της αρχής της ισοδυναμίας. Αυστηρά μιλώντας, όλες οι μετρήσεις της βαρυτικής διαστολής του χρόνου είναι δοκιμές της ασθενής εκδοχής της εν λόγω αρχής, όχι της ίδιας της γενικής σχετικότητας. Μέχρι στιγμής, η γενική σχετικότητα έχει περάσει όλες τις δοκιμές παρατήρησης.[32]
Αστροφυσικές εφαρμογές
[Επεξεργασία | επεξεργασία κώδικα]Τα μοντέλα που βασίζονται στη γενική σχετικότητα διαδραματίζουν σημαντικό ρόλο στην αστροφυσική , και η επιτυχία αυτών των μοντέλων είναι η περαιτέρω απόδειξη για την εγκυρότητα της θεωρίας.
Βαρυτικός εστιασμός
[Επεξεργασία | επεξεργασία κώδικα]
Δεδομένου ότι το φως εκτρέπεται σε ένα βαρυτικό πεδίο, είναι πιθανόν για το φως ενός μακρινού αντικειμένου να φτάσει σε ένα παρατηρητή ακολουθώντας δύο ή περισσότερες διαδρομές. Για παράδειγμα, το φως από ένα πολύ μακρινό αντικείμενο όπως ένα κβάζαρ μπορεί να περάσει κατά μήκος της μιας πλευράς ενός μεγάλου γαλαξία και να εκτρέπεται ελαφρά έτσι ώστε να φθάσει σε έναν παρατηρητή στη Γη, ενώ το φως που διέρχεται κατά μήκος της απέναντι πλευράς του ίδιου γαλαξία εκτρέπεται επίσης, φτάνοντας στον ίδιο παρατηρητή από μια ελαφρώς διαφορετική κατεύθυνση. Ως εκ τούτου, ο συγκεκριμένος παρατηρητής θα βλέπει ένα αστρονομικό αντικείμενο σε δύο διαφορετικά σημεία στο νυχτερινό ουρανό. Αυτό το είδος της εστιασμού είναι αρκετά γνωστό, όταν πρόκειται για οπτικούς φακούς, και συνεπώς η αντίστοιχη βαρυτική επίδραση ονομάζεται βαρυτικός εστιασμός.[33]
Η παρατηρησιακή αστρονομία χρησιμοποιεί τα αποτελέσματα του εστιασμού σαν ένα σημαντικό εργαλείο για την εξαγωγή των ιδιοτήτων του εστιαζόμενου αντικειμένου. Ακόμη και σε περιπτώσεις όπου αυτό το αντικείμενο δεν είναι άμεσα ορατό, το σχήμα μιας εστιασμένης εικόνας παρέχει πληροφορίες σχετικά με την κατανομή της μάζας που είναι υπεύθυνη για την εκτροπή του φωτός. Πιο συγκεκριμένα, ο βαρυτικός εστιασμός παρέχει έναν τρόπο για να μετρηθεί η κατανομή της σκοτεινής ύλης, η οποία δεν εκπέμπει φως και μπορεί να παρατηρηθεί μόνο από τις βαρυτικές επίδρασεις της. Μια ιδιαίτερα ενδιαφέρουσα εφαρμογή είναι οι παρατηρήσεις μεγάλης-κλίμακας, όπου οι εστιαζόμενες μάζες απλώνονται πάνω από ένα σημαντικό τμήμα του ορατού σύμπαντος, και μπορεί να χρησιμοποιηθεί για τη λήψη πληροφοριών σχετικά με τις ιδιότητες μεγάλης-κλίμακας και εξέλιξη του Κόσμου μας.[34]
Τα βαρυτικά κύματα
[Επεξεργασία | επεξεργασία κώδικα]Τα βαρυτικά κύματα, μια άμεση συνέπεια της θεωρίας του Αϊνστάιν, είναι στρεβλώσεις της γεωμετρίας του ίδιου του χώρου που διαδίδονται με την ταχύτητα του φωτός, και μπορούν να θεωρηθούν ως κυματισμοί στον χωροχρόνο. Δεν πρέπει να συγχέονται με τα κύματα βαρύτητας της ρευστομηχανικής, τα οποία είναι μια διαφορετική έννοια (κυματισμοί του ρευστού).
Έμμεσα, η επίδραση των βαρυτικών κυμάτων έχει ανιχνευθεί σε παρατηρήσεις συγκεκριμένων δυαδικών αστέρων. Τέτοια ζεύγη αστέρων βρίσκονται σε τροχιά μεταξύ τους και καθώς το κάνουν, χάνουν σταδιακά ενέργεια εκπέμποντας βαρυτικά κύματα. Για τα συνηθισμένα άστρα σαν τον Ήλιο, αυτή η απώλεια ενέργειας θα είναι πολύ μικρή για να είναι ανιχνεύσιμη. Όμως, αυτή η απώλεια ενέργειας παρατηρήθηκε το 1974 σε ένα δυαδικό πάλσαρ που ονομάζεται PSR1913 +16. Σε ένα τέτοιο σύστημα, ένα από τα δύο περιστρεφόμενα αστέρια είναι ένα πάλσαρ. Αυτό έχει δύο συνέπειες: ένα πάλσαρ είναι ένα εξαιρετικά πυκνό αντικείμενο γνωστό ως αστέρας νετρονίων, για το οποίο η εκπομπή βαρυτικών κυμάτων είναι πολύ ισχυρότερη από ότι για τους απλούς ατέρες. Επίσης, ένα πάλσαρ εκπέμπει μια στενή δέσμη ηλεκτρομαγνητικής ακτινοβολίας από τους μαγνητικούς πόλους του. Καθώς το πάλσαρ περιστρέφεται, η δέσμη του σαρώνει πάνω στη Γη όπου παρατηρείται σαν μία τακτική σειρά ραδιοπαλμών, ακριβώς όπως ένα πλοίο στη θάλασσα παρατηρεί τις τακτικές λάμψεις από την περιστροφόμενο φως σε ένα φάρο. Αυτό το τακτικό μοτίβο των ραδιοπαλμών λειτουργεί ως ένα εξαιρετικά ακριβές "ρολόι". Μπορεί να χρησιμοποιηθεί για να χρονομετρηθεί η περίοδος της τροχιάς του δυαδικού άστρου και αντιδρά με ευαισθησία σε στρεβλώσεις του χωροχρόνου στην άμεση γειτονιά του.
Στους εξερευνητές του PSR1913 +16, Russell Hulse και Joseph Taylor, απονεμήθηκε το βραβείο Νόμπελ Φυσικής το 1993. Από τότε, αρκετά άλλα δυαδικά πάλσαρ έχουν ανακαλυφθεί. Τα πιο χρήσιμα είναι εκείνα στα οποία και τα δύο άστρα είναι πάλσαρ, δεδομένου ότι παρέχουν τις πιο ακριβείς δοκιμές της γενικής σχετικότητας.[35]
Επί του παρόντος, ένας σημαντικός στόχος της έρευνας στη σχετικότητα είναι η άμεση ανίχνευση των βαρυτικών κυμάτων. Για το σκοπό αυτό, μια σειρά από επίγειους ανιχνευτές βαρυτικών κυμάτων είναι σε λειτουργία, ενώ μια αποστολή για να ξεκινήσει ένας διαστημικός ανιχνευτής LISA βρίσκεται υπό ανάπτυξη, με πρόδρομη αποστολή το LISA Pathfinder που αναμένεται να ξεκινήσει το 2015. Εάν ανιχνευθούν τα κύματα βαρύτητας, θα μπορούσαν να χρησιμοποιηθούν για τη συλλογή πληροφοριών σχετικά με συμπαγή αντικείμενα όπως τα αστέρια νετρονίων και μαύρες τρύπες, καθώς επίσης και να εξετάσει την κατάσταση του πρώιμου σύμπαντος κλάσματα του δευτερολέπτου μετά τη Μεγάλη Έκρηξη (Big Bang).[36]
Μαύρες τρύπες
[Επεξεργασία | επεξεργασία κώδικα]
Όταν η μάζα συγκεντρώνεται μέσα σε μία επαρκώς συμπαγή περιοχή του χώρου, η γενική σχετικότητα προβλέπει το σχηματισμό μιας μαύρη τρύπα - μία περιοχή του χώρου με βαρυτική επίδραση τόσο ισχυρή ώστε ούτε το φως να μη μπορεί να διαφύγει. Συγκεκριμένοι τύποι μαύρων τρυπών πιστεύεται οτι είναι το τελικό στάδιο στην εξέλιξη των μεγάλων αστέρων. Απ΄την άλλη, υπερμεγέθεις μαύρες τρύπες με τη μάζα εκατομμυρίων ή και δισεκατομμυρίων ηλιακών μαζών θεωρούνται ότι υπάρχουν στους πυρήνες των περισσότερων γαλαξιών και παίζουν καθοριστικό ρόλο στα τωρινά μοντέλα του πως σχηματίστηκαν οι γαλαξίες στη διάρκεια δισεκατομμυρίων ετών που πέρασαν.[37]
Η ύλη που πέφτει σε ένα συμπαγές αντικείμενο είναι ένας από τους πιο αποτελεσματικούς μηχανισμούς για την απελευθέρωση ενέργειας, με τη μορφή της ακτινοβολίας, ενώ ύλη που πέφτει μέσα σε μαύρες τρύπες θεωρείται υπεύθυνη για μερικά από τα λαμπρότερα αστρονομικά φαινόμενα. Αξιοσημείωτα παραδείγματα με μεγάλο ενδιαφέρον για τους αστρονόμους είναι τα κβάζαρ και άλλοι τύποι ενεργών γαλαξιακών πυρήνων. Υπό τις κατάλληλες συνθήκες, η ύλη που πέφτει και συσσωρεύεται γύρω από μια μαύρη τρύπα μπορεί να οδηγήσει στο σχηματισμό πιδάκων, στους οποίους στγκεντρωμένες δέσμες ύλης διαφεύγουν μακριά στο διάστημα με ταχύτητες κοντά σε αυτήν του φωτός.[38]
Υπάρχουν αρκετές ιδιότητες που κάνουν τις μαύρες τρύπες τις πλέον υποσχόμενες πηγές των βαρυτικών κυμάτων. Ένας λόγος είναι ότι οι μαύρες τρύπες είναι τα πιο συμπαγή αντικείμενα που μπορούν να βρίσκονται σε τροχιά μεταξύ τους ως μέρος ενός δυαδικού συστήματος. Σαν αποτέλεσμα, τα βαρυτικά κύματα που εκπέμπονται από ένα τέτοιο σύστημα είναι ιδιαίτερα ισχυρά. Ένας άλλος λόγος προκύπτει από τα αποκαλούμενα θεωρήματα μοναδικότητας της μαύρης τρύπας: με την πάροδο του χρόνου, οι μαύρες τρύπες διατηρούν μόνο ένα ελάχιστο σύνολο διακριτικών χαρακτηριστικών (εφόσον τα διαφορετικά στυλ μαλλιών είναι καθοριστικά στοιχεία που δίνουν σε διαφορετικούς ανθρώπους διαφορετικές εμφανίσεις, αυτά τα θεωρήματα έχουν γίνει γνωστά ως θεωρήματα "χωρίς μαλλιά" ("no-hair") ). Για παράδειγμα, μακροπρόθεσμα, η κατάρρευση ενός υποθετικού κύβου ύλης δεν θα οδηγήσει στο σχηματισμό μιας μαύρης τρύπας σχήματος κύβου. Αντίθετα, η προκύπτουσα μαύρη τρύπα δε θα διακρίνεται από μια μαύρη τρύπα που σχηματίστηκε από την κατάρρευση μιας σφαιρικής μάζας, αλλά με μια σημαντική διαφορά: κατά τη μετάβασή της σε σφαιρικό σχήμα, η μαύρη τρύπα που σχηματίζεται από την κατάρρευση ενός κύβου θα εκπέμπει βαρυτικά κύματα.[39]
Κοσμολογία
[Επεξεργασία | επεξεργασία κώδικα]Μία από τις πιο σημαντικές πτυχές της γενικής σχετικότητας είναι ότι μπορεί να εφαρμοστεί στο σύμπαν ως σύνολο. Ένα βασικό σημείο είναι ότι στις μεγάλες κλίμακες, το σύμπαν μας φαίνεται να έχει κατασκευαστεί σύμφωνα με πολύ απλές γραμμές. Όλες οι τρέχουσες παρατηρήσεις υποδεικνύουν ότι κατά μέσο όρο, η δομή του σύμπαντος πρέπει να είναι περίπου η ίδια, ανεξάρτητα από τη θέση ενός παρατηρητή ή την κατεύθυνση της παρατήρησης. Το σύμπαν είναι προσεγγιστικά ομοιογενές και ισότροπο. Τέτοια σχετικά απλά σύμπαντα μπορούν να περιγραφούν από απλές λύσεις των εξισώσεων του Αϊνστάιν. Τα τρέχοντα κοσμολογικά μοντέλα του σύμπαντος προκύπτουν από το συνδυασμό αυτών των απλών λύσεων της γενικής σχετικότητας με τις θεωρίες που περιγράφουν τις ιδιότητες της ύλης του σύμπαντος, δηλαδή την Θερμοδυναμική, την πυρηνική φυσική και την σωματιδιακή φυσική. Σύμφωνα με αυτά τα μοντέλα, το σημερινό σύμπαν μας προέκυψε από μια εξαιρετικά πυκνή και υψηλής θερμοκρασίας κατάσταση, τη Μεγάλη Έκρηξη (Big Bang), περίπου πριν 14 δισεκατομμύρια χρόνια και επεκτείνεται από τότε.[40]
Οι εξισώσεις του Αϊνστάιν μπορούν να γενικευθούν με την προσθήκη ενός όρου που ονομάζεται κοσμολογική σταθερά. Όταν αυτός ο όρος είναι παρών, ο κενός χώρος ενεργεί ως πηγή έλξης ή ασυνήθιστα, ως απωθητική βαρύτητα. Ο Einstein εισήγαγε αρχικά τον όρο αυτό στην πρωτοποριακή εργασία του 1917 για την κοσμολογία, με ένα πολύ συγκεκριμένο κίνητρο: η κοσμολογική σκέψη εκείνης της εποχής θεωρούσε το σύμπαν στατικό και ο πρόσθετος όρος απαιτούνταν για την κατασκευή στατικών συμπαντικών μοντέλων στο πλαίσιο της γενικής σχετικότητας. Όταν έγινε φανερό ότι το σύμπαν δεν είναι στατικό αλλά επεκτείνεται, ο Αϊνστάιν γρήγορα απέρριψε αυτόν τον όρο, πρόωρα όπως γνωρίζουμε σήμερα. Από το 1998 περίπου και μετά, σταθερά συσσωρευόμενα αστρονομικά στοιχεία έχουν δείξει ότι η διαστολή του σύμπαντος επιταχύνεται με τρόπο που υποδηλώνει την παρουσία μιας κοσμολογικής σταθεράς ή ισοδύναμα, μιας σκοτεινής ενέργειας με συγκεκριμένες ιδιότητες που διαπερνά όλο το χώρο.[41]
Η σύγχρονη έρευνα: η γενική σχετικότητα και παραπέρα
[Επεξεργασία | επεξεργασία κώδικα]Η γενική σχετικότητα είναι πολύ επιτυχής παρέχοντας ένα πλαίσιο για ακριβή μοντέλα που περιγράφουν μια εντυπωσιακή σειρά από φυσικά φαινόμενα. Από την άλλη πλευρά, υπάρχουν πολλά ενδιαφέροντα ανοικτά ερωτήματα, και ειδικότερα, η θεωρία ως σύνολο είναι σχεδόν σίγουρα ατελής.[42]
Σε αντίθεση με όλες τις άλλες σύγχρονες θεωρίες των θεμελιωδών αλληλεπιδράσεων, η γενική σχετικότητα είναι μια κλασική θεωρία: δεν περιλαμβάνει τις επιπτώσεις της κβαντικής φυσικής. Η αναζήτηση για μια κβαντική έκδοση της γενικής σχετικότητας αντιμετωπίζει ένα από τα πιο θεμελιώδη αναπάντητα ερωτήματα της φυσικής. Ενώ υπάρχουν υποσχόμενοι υποψήφιοι για μια τέτοια θεωρία της κβαντικής βαρύτητας, και ιδίως η θεωρία χορδών και η κβαντική βαρύτητα βρόχων, δεν υπάρχει επί του παρόντος καμία συνεπής και πλήρης θεωρία. Εδώ και καιρό υπάρχει η ελπίδα ότι μια θεωρία της κβαντικής βαρύτητας θα εξαλείψει επίσης ένα άλλο προβληματικό χαρακτηριστικό της γενικής σχετικότητας: την παρουσία των ιδιομορφιών του χωροχρόνου. Αυτές οι ανωμαλίες είναι τα σύνορα ("αιχμηρά άκρα") του χωροχρόνου στο οποίο η γεωμετρία γίνεται ασαφής, με συνέπεια η γενική σχετικότητα η ίδια να χάνει τη δύναμη πρόβλεψής της. Επιπλέον, υπάρχουν λεγόμενα θεωρήματα ανωμαλίας που προβλέπουν ότι τέτοιες ανωμαλίες πρέπει να υπάρχουν μέσα στο σύμπαν, αν οι νόμοι της γενικής σχετικότητας ίσχυαν χωρίς οποιεσδήποτε κβαντικές τροποποιήσεις. Τα πιο γνωστά παραδείγματα είναι οι ανωμαλίες που σχετίζονται με σύμπαντα μοντέλο που περιγράφουν τις μαύρες τρύπες και την αρχή του σύμπαντος.[43]
Άλλες προσπάθειες για να τροποποιηθεί η γενική σχετικότητα έχουν γίνει στο πλαίσιο της κοσμολογίας. Στα σύγχρονα κοσμολογικά μοντέλα, η περισσότερη ενέργεια στο σύμπαν είναι σε μορφές που δεν έχουν ανιχνευτεί άμεσα ποτέ, δηλαδή η σκοτεινή ενέργεια και η σκοτεινή ύλη. Υπήρξαν πολλές αμφιλεγόμενες προτάσεις για να αποφευχθεί η ανάγκη για αυτές τις αινιγματικές μορφές ύλης και ενέργειας, τροποποιώντας τους νόμους που διέπουν τη βαρύτητα και τη δυναμική της κοσμικής διαστολής, για παράδειγμα Τροποποιημένη Νευτώνεια Δυναμική.[44]
Πέρα από τις προκλήσεις των κβαντικών επιπτώσεων και της κοσμολογίας, η έρευνα για τη γενική σχετικότητα είναι πλούσια με δυνατότητες για περαιτέρω διερεύνηση: μαθηματικοί σχετικιστές εξερευνούν τη φύση των ανωμαλιών και τις θεμελιώδεις ιδιότητες των εξισώσεων του Αϊνστάιν,[45] λειτουργούν όλο και πιο ολοκληρωμένες προσομοιώσεις υπολογιστών των συγκεκριμένων χωροχρόνων (όπως εκείνες που περιγράφουν συγχωνευόμενες μαύρες τρύπες),[46] και ο αγώνας για την πρώτη άμεση ανίχνευση των βαρυτικών κυμάτων συνεχίζεται με γοργούς ρυθμούς.[47] Περισσότερα από ενενήντα χρόνια μετά την έκδοση της θεωρίας για πρώτη φορά, η έρευνα είναι πιο δραστήρια από ποτέ.[48]
Σημειώσεις
[Επεξεργασία | επεξεργασία κώδικα]- ↑ -Η Κατασκευή της Σύγχρονης Επιστήμης: Μηχανισμοί και Μηχανικοί, από τον Richard S. Westfall. Cambridge University Press. 1978
- ↑ Η εξέλιξη αυτή εντοπίστηκε π.χ. στο Renn 2005, σ.110ff., Στα κεφάλαια 9 έως 15 του Pais 1982, και στο Janssen 2005. Μία περίληψη της νευτώνειας βαρύτητας μπορεί να βρεθεί στο Schutz 2003, κεφάλαια 2-4. Είναι αδύνατο να πούμε αν το πρόβλημα της νευτώνειας βαρύτητας διέσχισε το μυαλό του Αϊνστάιν πριν από το 1907, αλλά από δική του παραδοχή, η πρώτη σοβαρή προσπάθεια του να συμβιβάσει τη θεωρία αυτή με ειδική σχετικότητα χρονολογείται αυτή τη χρονιά, βλ. Pais 1982, σ.178.
- ↑ Αυτό περιγράφεται αναλυτικά στο κεφάλαιο 2 του Wheeler 1990
- ↑ Ενώ η αρχή της ισοτιμίας εξακολουθεί να είναι μέρος της σύγχρονης έκθεσης της γενικής σχετικότητας, υπάρχουν ορισμένες διαφορές μεταξύ στη σύγχρονη εκδοχή και πρωτότυπη ιδέα του Αϊνστάιν, βλ. Norton 1985.
- ↑ Π.χ. Janssen 2005, σ.64f. Ο ίδιος ο Αϊνστάιν εξηγεί αυτό στο κεφάλαιο XX στο μη-τεχνικό βιβλίο του Αϊνστάιν 1961. Μετά τις ιδέες από τον Ernst Mach, ο Αϊνστάιν διερεύνησε επίσης τις φυγοκεντρικές δυνάμεις και τη βαρυτική τους αναλογία, βλ. Stachel 1989.
- ↑ Ο Einstein το εξηγεί αυτό στην ενότητα XX του Einstein 1961.Θεώρησε ένα αντικείμενο να "αναστέλλεται" με ένα σχοινί από την οροφή ενός δωματίου, πάνω σε έναν πύραυλο επιτάχυνσης: από το εσωτερικό του δωματίου φαίνεται ότι η βαρύτητα έλκει το αντικείμενο προς τα κάτω με δύναμη ανάλογη με τη μάζα του, αλλά από έξω φαίνεται ότι το σχοινί είναι η απλή μεταφορά της επιτάχυνσης του πυραύλου με το αντικείμενο, και θα πρέπει, συνεπώς, να ασκήσει μόνο την «δύναμη».
- ↑ Πιο συγκεκριμένα, οι υπολογισμοί του Einstein,bοι οποίοι περιγράφονται στο κεφάλαιο 11b του Pais 1982, χρησιμοποιεί την αρχή της ισοδυναμίας, της ισοδυναμίας την δυνάμεων βαρύτητας και αδράνειας,και τα αποτελέσματα της ειδικής σχετικότητας για τη διάδοση του φωτός και για την ταχύτερη παρατήρηση (το τελευταίο με την εξέταση, σε κάθε στιγμή, το στιγμιαίο αδρανειακό σύστημα αναφοράς σχετίζεται με μια τέτοια επιταχυνόμενη παρατήρηση).
- ↑ Η επίδραση αυτή μπορεί να προέρχεται απευθείας μέσα από την ειδική συχνότητα,είτε παρατηρώντας την αντίστοιχη κατάσταση των δύο παρατηρητών σε μια επιτάχυνση πυραύλου-πλοίου ή παρατηρώντας μια πτώση ασανσέρ: και στις δυο περιπτώσεις, η μετατόπιση της συχνότητας έχει ισοδύναμη περιγραφή ως μετατόπιση Doppler μεταξύ ορισμένων αδρανειακών συστημάτων. Για απλά παράγωγα αυτού, βλέπε Harrison 2002.
- ↑ Δείτε το κεφάλαιο 12 του Mermin 2005.
- ↑ βλ. Ehlers & Rindler 1997: για μια μη-τεχνική παρουσίαση, δείτε Pössel 2007.
- ↑ Αυτά και άλλα παλιρροιακά φαινόμενα περιγράφονται στο Wheeler 1990, σελίδες 83–91.
- ↑ Οι παλίρροιες και η γεωμετρική τους ερμηνεία εξηγείται στο κεφάλαιο 5 το Wheeler 1990. Αυτό το κομμάτι της ιστορικής εξέλιξης εντοπίζεται στην Pais 1982, section 12b, στο τμήμα 12b.
- ↑ Για στοιχειώδη παρουσιάσεις της έννοιας του χωροχρόνου, ανατρέξτε στην πρώτη ενότητα του κεφαλαίου 2 του Thorne 1994, και Greene 2004, σσ. 47–61. Πιο ολοκληρωμένες κατεργασίες σε ένα αρκετά στοιχειώδες επίπεδο μπορεί να βρεθεί π.χ. στο Mermin 2005 και στο Wheeler 1990, κεφάλαια 8 και 9.
- ↑ Δείτε Wheeler 1990, κεφάλαια 8 και 9, για ζωντανές απεικονίσεις των καμπύλων χωροχρόνου.
- ↑ Ο αγώνας του Einstein για την εύρεση των σωστών εξισώσεων επιπέδου εντοπίζεται στα κεφάλαια 13-15 του Pais 1982.
- ↑ π.χ. σ. xi στο Wheeler 1990 .
- ↑ Μια εμπεριστατωμένη, διαθέσιμη ακόμη έκθεση της βασικής διαφορικής γεωμετρίας και της εφαρμογής της στη γενική σχετικότητα μπορεί να βρεθεί Geroch 1978.
- ↑ Δείτε το κεφάλαιο 10 στο Wheeler 1990.
- ↑ Στην πραγματικότητα, ξεκινώντας από την πλήρη θεωρία, η εξίσωση του Einstein μπορεί να χρησιμοποιηθεί για to derive these more complicated laws of motion for matter as a consequence of geometry, but deriving from this the motion of idealized test particles is a highly non-trivial task βλ. Poisson 2004.
- ↑ Μια απλή εξήγηση της μάζας-ενέργειας ισοδυναμίας μπορεί να βρεθεί στα σημεία 3.8 και 3.9 του Giulini 2005.
- ↑ Δείτε το κεφάλαιο 6 του Wheeler 1990.
- ↑ Για έναν πιο λεπτομερή ορισμό της μετρικής, αλλά έναν που είναι όχι τόσο επίσημος από μια παρουσίαση βιβλίου, δείτε το κεφάλαιο 14.4 του Penrose 2004.
- ↑ Η γεωμετρική ερμηνεία των εξισώσεων του Einstein έχει διερευνηθεί στα κεφάλαια 7 και 8 του Wheeler 1990: βλ. box 2.6 στο Thorne 1994. Μια εισαγωγή χρησιμοποιώντας μόνο απλά μαθηματικά δίνεται στο κεφάλαιο 19 του Schutz 2003.
- ↑ Οι πιο σημαντικές λύσεις αναφέρονται σε κάθε βιβλίο της γενικής σχετικότητας: για την (τεχνική) περίληψη των σημερινών μας γνώσεων, βλ. Friedrich 2005.
- ↑ Πιο συγκεκριμένα, αυτά είναι VLBI μετρήσεις των θέσεων των πλανητών: δείτε κεφάλαιο 5 από Will 1993 και το τμήμα 3.5 από Will 2006.
- ↑ Για τις ιστορικές μετρήσεις, δείτε Hartl 2005, Kennefick 2005, και Kennefick 2007: η αυθεντική παραγωγή του Soldner στο πλαίσιο της θεωρίας του Νεύτων βρίσκεται στο Soldner 1804. Για τις πιο ακριβείς μετρήσεις μέχρι σήμερα, δείτε Bertotti 2005.
- ↑ Δείτε Kennefick 2005 και στο κεφάλαιο 3 του Will 1993. Για τις μετρήσεις του Sirius B, δείτε Trimble & Barstow 2007.
- ↑ Pais 1982, Mercury στις σελ. 253-254,η άνοδος της φήμης του Αϊνστάιν στα τμήματα 16b και 16c.
- ↑ Everitt, C.W.F.; Parkinson, B.W. (2009), Gravity Probe B Science Results—NASA Final Report, http://einstein.stanford.edu/content/final_report/GPB_Final_NASA_Report-020509-web.pdf, ανακτήθηκε στις 2009-05-02
- ↑ Kramer 2004.
- ↑ Παγκόσμιο σύστημα εντοπισμού θέσης μπορεί να βρεθεί στο Ashby 2002: λεπτομέρειες δίνονται στο Ashby 2003.
- ↑ Μια προσιτή εισαγωγή στις δοκιμές της γενικής σχετικότητας βρίσκεται στο Will 1993.
- ↑ Η γεωμετρία των καταστάσεων αυτών έχει διερευνηθεί στο κεφάλαιο 23 του Schutz 2003.
- ↑ Εισαγωγές του βαρυτικού εστιασμού και εφαρμογές του μπορούν να βρεθούν στις ιστοσελίδες Newbury 1997 και Lochner 2007.
- ↑ Schutz 2003, σελ.317-321, Bartusiak 2000, σελ. 70-86.
- ↑ Η αναζήτηση για τα κύματα βαρύτητας περιγράφεται στο Bartusiak 2000 και στο Blair & McNamara 1997.
- ↑ Για μια επισκόπηση της ιστορίας των μαύρων τρυπών από το ξεκίνημα στις αρχές του 20ου αιώνα μέχρι τη σύγχρονη εποχή, δείτε την ευανάγνωστη άποψη από Thorne 1994.
- ↑ Δείτε το κεφάλαιο 8 από Sparkeand Gallagher 2007 και Disney 1998. Επίσης δείτε Rodson 1996.
- ↑ Μια στοιχειώδης εισαγωγή στο θεώρημα μοναδικότητας της μαύρης τρύπας μπορεί να βρεθεί στο Chrusciel 2006 και στο Thorne 1994, σελ. 272-286.
- ↑ Αναλυτικές πληροφορίες μπορούν να βρεθούν στο Ned Wright's Cosmology Tutorial and FAQ, Wright 2007: μια ευανάγνωστη εισαγωγή είναι το Hogan 1999. Χρησιμοποιώντας προπτυχιακά μαθηματικά, αλλά αποφεύγοντας τα προηγμένα μαθηματικά εργαλεία της γενικής σχετικότητας, το Berry 1989 παρέχει μια πιο ολοκληρωμένη παρουσίαση.
- ↑ Το αυθεντικό έγγραφο του Einstein είναι το Einstein 1917: καλές περιγραφές των πιο σύγχρονων εξελίξεων μπορείτε να βρείτε στο Cowen 2001 και στο Caldwell 2004.
- ↑ βλ. Maddox: Penrose 2004, τμήμα 34.1 και κεφάλαιο 30.
- ↑ Με έμφαση στη θεωρία των χορδών, η αναζήτηση για την κβαντική βαρύτητα περιγράφεται στο Greene 1999: από τη σκοπιά της κβαντικής βαρύτητας βρόχων, δείτε Smolin 2001.
- ↑ Για τη σκοτεινή ύλη, δείτε Milgrom 2002. Για τη σκοτεινή ενέργεια, δείτε Caldwell 2004.
- ↑ Δείτε Friedrich 2005.
- ↑ Μια ανασκόπηση των διαφορων προβλημάτων και των τεχνικών που αναπτύσσονται για την αντιμετώπισή τους, δείτε Lehner 2002.
- ↑ Δείτε Bartusiak 2000.
- ↑ Ένα καλό σημείο εκκίνησης για ένα στιγμιότυπο της σημερινής έρευνας ως προς τη σχετικότητα είναι το ηλεκτρονικό περιοδικό Living Reviews in Relativity Αρχειοθετήθηκε 2016-12-27 στο Wayback Machine..
Παραπομπές
[Επεξεργασία | επεξεργασία κώδικα]- Ashby, Neil (2002), «Relativity and the Global Positioning System», Physics Today 55 (5): 41–47, doi:, http://www.ipgp.jussieu.fr/~tarantola/Files/Professional/GPS/Neil_Ashby_Relativity_GPS.pdf
- Ashby, Neil (2003), «Relativity in the Global Positioning System», Living Reviews in Relativity 6: 1, doi:, http://relativity.livingreviews.org/Articles/lrr-2003-1/index.html, ανακτήθηκε στις 2007-07-06
- Bartusiak, Marcia (2000), Einstein's Unfinished Symphony: Listening to the Sounds of Space-Time, Berkley, ISBN 978-0-425-18620-6
- Berry, Michael V. (1989), Principles of Cosmology and Gravitation (2nd έκδοση), Institute of Physics Publishing, ISBN 0-85274-037-9
- Bertotti, Bruno (2005), «The Cassini Experiment: Investigating the Nature of Gravity», στο: Renn, Jürgen, επιμ., One hundred authors for Einstein, Wiley-VCH, σελ. 402–405, ISBN 3-527-40574-7
- Blair, David; McNamara, Geoff (1997), Ripples on a Cosmic Sea. The Search for Gravitational Waves, Perseus, ISBN 0-7382-0137-5, https://archive.org/details/isbn_9780738201375
- Caldwell, Robert R.; Crittenden, R (2004), «Dark Energy», Physics World 17(5) (6969): 37–42, doi:, PMID 14702078, http://physicsweb.org/articles/world/17/5/7
- Chrusciel, Piotr (2006), «How many different kinds of black hole are there?», Einstein Online, http://www.einstein-online.info/spotlights/bh_uniqueness/, ανακτήθηκε στις 2007-07-15
- Cowen, Ron (2001), «A Dark Force in the Universe», Science News (Society for Science &) 159 (14): 218, doi:
- Disney, Michael (1998), «A New Look at Quasars», Scientific American 6 (6): 52–57, doi:
- Ehlers, Jürgen; Rindler, Wolfgang (1997), «Local and Global Light Bending in Einstein's and other Gravitational Theories», General Relativity and Gravitation 29 (4): 519–529, doi:
- Einstein, Albert (1917), «Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie», Sitzungsberichte der Preußischen Akademie der Wissenschaften: 142
- Einstein, Albert (1961), Relativity. The special and general theory, Crown Publishers, http://www.gutenberg.org/etext/5001
- Friedrich, Helmut (2005), «Is general relativity 'essentially understood'?», Annalen Phys. 15 (1–2): 84–108, doi:
- Geroch, Robert (1978), General relativity from A to B, University of Chicago Press, ISBN 0-226-28864-1
- Giulini, Domenico (2005), Special relativity. A first encounter, Oxford University Press, ISBN 0-19-856746-4
- Gnedin, Nickolay Y. (2005), «Digitizing the Universe», Nature 435 (7042): 572–573, doi:, PMID 15931201
- Greene, Brian (1999), The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory, Vintage, ISBN 0-375-70811-1
- Greene, Brian (2004), The Fabric of the Cosmos: Space, Time, and the Texture of Reality, A. A. Knopf, ISBN 0-375-41288-3
- Harrison, David M. (2002), A Non-mathematical Proof of Gravitational Time Dilation, http://www.upscale.utoronto.ca/GeneralInterest/Harrison/GenRel/TimeDilation.pdf, ανακτήθηκε στις 2007-05-06
- Hartl, Gerhard (2005), «The Confirmation of the General Theory of Relativity by the British Eclipse Expedition of 1919», στο: Renn, Jürgen, επιμ., One hundred authors for Einstein, Wiley-VCH, σελ. 182–187, ISBN 3-527-40574-7
- Hogan, Craig J. (1999), The Little Book of the Big Bang. A Cosmic Primer, Springer, ISBN 0-387-98385-6
- Janssen, Michel (2005), «Of pots and holes: Einstein's bumpy road to general relativity», Ann. Phys. (Leipzig) 14 (S1): 58–85, doi:, https://netfiles.umn.edu/users/janss011/home%20page/potsandholes.pdf, ανακτήθηκε στις 2016-01-14
- Kennefick, Daniel (2005), «Astronomers Test General Relativity: Light-bending and the Solar Redshift», στο: Renn, Jürgen, επιμ., One hundred authors for Einstein, Wiley-VCH, σελ. 178–181, ISBN 3-527-40574-7
- Kennefick, Daniel (2007), «Not Only Because of Theory: Dyson, Eddington and the Competing Myths of the 1919 Eclipse Expedition», Proceedings of the 7th Conference on the History of General Relativity, Tenerife, 2005, 0709, σελ. 685
- Kramer, Michael (2004), «Millisecond Pulsars as Tools of Fundamental Physics», στο: Karshenboim, S. G.; Peik, E., επιμ., Astrophysics, Clocks and Fundamental Constants (Lecture Notes in Physics Vol. 648), Springer, σελ. 33–54 (E-Print at astro-ph/0405178 Αρχειοθετήθηκε 2017-11-05 στο Wayback Machine.)
- Lehner, Luis (2002), «Numerical Relativity: Status and Prospects», Proceedings of the 16th International Conference on General Relativity and Gravitation, held 15–21 July 2001 in Durban, σελ. 210, doi:, ISBN 978-981-238-171-2
- Lochner, Jim, επιμ.. (2007), «Gravitational Lensing», Imagine the Universe website (NASA GSFC), http://imagine.gsfc.nasa.gov/docs/features/news/grav_lens.html, ανακτήθηκε στις 2007-06-12
- Maddox, John (1998), What Remains To Be Discovered, Macmillan, ISBN 0-684-82292-X, https://archive.org/details/whatremainstobed00madd
- Mermin, N. David (2005), It's About Time. Understanding Einstein's Relativity, Princeton University Press, ISBN 0-691-12201-6
- Milgrom, Mordehai (2002), «Does dark matter really exist?», Scientific American 287 (2): 30–37, doi:, http://www.sciamdigital.com/index.cfm?fa=Products.ViewIssuePreview&ARTICLEID_CHAR=724C1E4B-FFD5-46F4-963E-7610EC8B7EC&sc=I100322, ανακτήθηκε στις 2016-01-14
- Norton, John D. (1985), «What was Einstein's principle of equivalence?», Studies in History and Philosophy of Science 16 (3): 203–246, doi:, http://www.pitt.edu/~jdnorton/papers/ProfE_re-set.pdf, ανακτήθηκε στις 2007-06-11
- Newbury, Pete (1997), Gravitational lensing webpages, http://www.iam.ubc.ca/old_pages/newbury/lenses/research.html, ανακτήθηκε στις 2007-06-12
- Nieto, Michael Martin (2006), «The quest to understand the Pioneer anomaly», EurophysicsNews 37 (6): 30–34, doi:, http://www.europhysicsnews.com/full/42/article4.pdf, ανακτήθηκε στις 2016-01-14
- Pais, Abraham (1982), 'Subtle is the Lord ...' The Science and life of Albert Einstein, Oxford University Press, ISBN 0-19-853907-X, https://archive.org/details/subtleislordscie00pais
- Penrose, Roger (2004), The Road to Reality, A. A. Knopf, ISBN 0-679-45443-8, https://archive.org/details/roadtorealitycom00penr_0
- Pössel, M. (2007), «The equivalence principle and the deflection of light», Einstein Online, http://www.einstein-online.info/en/spotlights/equivalence_deflection/index.html, ανακτήθηκε στις 2007-05-06
- Poisson, Eric (2004), «The Motion of Point Particles in Curved Spacetime», Living Rev. Relativity 7, doi:, http://www.livingreviews.org/lrr-2004-6, ανακτήθηκε στις 2007-06-13
- Renn, Jürgen, επιμ.. (2005), Albert Einstein – Chief Engineer of the Universe: Einstein's Life and Work in Context, Berlin: Wiley-VCH, ISBN 3-527-40571-2
- Robson, Ian (1996), Active galactic nuclei, John Wiley, ISBN 0-471-95853-0
- Schutz, Bernard F. (2003), Gravity from the ground up, Cambridge University Press, ISBN 0-521-45506-5
- Smolin, Lee (2001), Three Roads to Quantum Gravity, Basic, ISBN 0-465-07835-4
- von Soldner, Johann Georg (1804), «Ueber die Ablenkung eines Lichtstrals von seiner geradlinigen Bewegung, durch die Attraktion eines Weltkörpers, an welchem er nahe vorbei geht», Berliner Astronomisches Jahrbuch: 161–172.
- Sparke, Linda S.; Gallagher, John S. (2007), Galaxies in the universe – An introduction, Cambridge University Press, ISBN 0-521-85593-4
- Springel, Volker; White, Simon D. M.; Jenkins, Adrian; Frenk, Carlos S.; Yoshida, N; Gao, L; Navarro, J; Thacker, R και άλλοι. (2005), «Simulations of the formation, evolution and clustering of galaxies and quasars», Nature 435 (7042): 629–636, doi:, PMID 15931216
- Stachel, John (1989), «The Rigidly Rotating Disk as the 'Missing Link in the History of General Relativity'», στο: Howard, D.; Stachel, J., επιμ., Einstein and the History of General Relativity (Einstein Studies, Vol. 1), Birkhäuser, σελ. 48–62, ISBN 0-8176-3392-8
- Thorne, Kip (1994), Black Holes and Time Warps: Einstein's Outrageous Legacy, W W Norton & Company, ISBN 0-393-31276-3
- Trimble, Virginia; Barstow, Martin (2007), «Gravitational redshift and White Dwarf stars», Einstein Online, http://www.einstein-online.info/spotlights/redshift_white_dwarfs/, ανακτήθηκε στις 2007-06-13
- Wheeler, John A. (1990), A Journey Into Gravity and Spacetime, Scientific American Library, San Francisco: W. H. Freeman, ISBN 0-7167-6034-7
- Will, Clifford M. (1993), Was Einstein Right?, Oxford University Press, ISBN 0-19-286170-0
- Will, Clifford M. (2006), «The Confrontation between General Relativity and Experiment», Living Rev. Relativity 9: 3, doi:, http://www.livingreviews.org/lrr-2006-3, ανακτήθηκε στις 2007-06-12
- Wright, Ned (2007), Cosmology tutorial and FAQ, University of California at Los Angeles, http://www.astro.ucla.edu/~wright/cosmolog.htm, ανακτήθηκε στις 2007-06-12
Επιπλέον Σύνδεσμοι
[Επεξεργασία | επεξεργασία κώδικα]Επιπλέον πόροι, μπορούν να βρεθούν στην προτεινόμενη βιβλιογραφία που εμπεριέχει περισσότερο προχωρημένο υλικό.
- Einstein Online Διαδικτυακός τόπος που χαρακτηρίζει τα άρθρα σχετικά με διάφορες πτυχές της σχετικιστικής φυσικής για ένα γενικό ακροατήριο, το οποίο φιλοξενείται από το Max Planck Institute for Gravitational Physics.
- NCSA Spacetime Wrinkles .Διαδικτυακός τόπος που παράγεται από την ομάδα της αριθμητικής σχετικότητας στο National Center for Supercomputing Applications , με μια στοιχειώδη εισαγωγή στη γενική σχετικότητα, μαύρες τρύπες και βαρυτικά κύματα.
| Στο λήμμα αυτό έχει ενσωματωθεί κείμενο από το λήμμα Introduction to general relativity της Αγγλικής Βικιπαίδειας, η οποία διανέμεται υπό την GNU FDL και την CC-BY-SA 4.0. (ιστορικό/συντάκτες). |
