Δεκάγραμμα

Κανονικό δεκάγραμμα

Κανονικό δεκάγραμμα (10/3)
Τύπος Κανονικό πολύγωνο
Πλευρές και κορυφές 10
Schläfli {10/3}  ή  t{5/3}
Coxeter-Dynkin  ή 
Συμμετρία Διεδρική D10
Εσωτερική γωνία 72°
Διπλό πολύγωνο το ίδιο
Ιδιότητες αστεροειδές, κυκλικό, ισόπλευρο, ισογώνιο, ισότοξο

Στη γεωμετρία, το δεκάγραμμα είναι ένα αστεροειδές πολύγωνο που έχει δέκα πλευρές. Υπάρχει μόνο ένα κανονικό δεκάγραμμα, που περιέχει τις κορυφές ενός κανονικού δεκαγώνου, αλλά συνδέεται σε κάθε τρίτο σημείο. Επισημαίνεται με το σύμβολο Schläfli {10/3}.[1]

Η λέξη δεκάγραμμα συνδυάζει το αριθμητικό πρόθεμα δέκα- με το επίθεμα -γραμμή.[2]

Κανονικό δεκάγραμμα

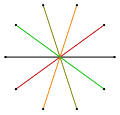
[Επεξεργασία | επεξεργασία κώδικα]

Για ένα κανονικό δεκάγραμμα με μήκος ακμής την μονάδα, οι αναλογίες των σημείων διέλευσης σε κάθε ακμή είναι όπως φαίνεται παρακάτω:

Συναφή σχήματα

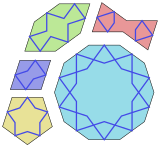
[Επεξεργασία | επεξεργασία κώδικα]

Ένα κανονικό δεκάγραμμα είναι ένα δεκάπλευρο πολύγραμμα, που επισημαίνεται με το σύμβολο Schläfli {10/n}, και περιέχει τις κορυφές ενός κανονικού δεκαγώνου. Μόνο ένα από τα πολυγράμματα αυτά, το {10/3}, έχει τη μορφή κανονικού αστεροειδούς πολυγώνου, αλλά υπάρχουν ακόμα τρία πολυγράμματα δέκα κορυφών, τα οποία μπορούν να ερμηνευθούν ως κανονικές ενώσεις:[3][4]

Κυρτό Ένωση Αστεροειδές Ενώσεις
{10/1} = {10} {10/2} = 2{5} {10/3} {10/4} = 2{5/2} {10/5} = 5{2}

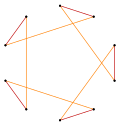
Με βαθύτερες περικοπές του κανονικού πενταγώνου και του πενταγράμμου μπορεί να παραχθούν ενδιάμεσες μορφές αστεροειδών πολυγώνων με δέκα ισαπέχουσες κορυφές και δύο μήκη ακμών που παραμένουν ισογώνιες (ανά δύο οι κορυφές μπορούν να μετατραπούν η μία στην άλλη με τη συμμετρία του σχήματος).[5][6][7]

Ισογώνιες περικοπές του πενταγώνου και του πενταγράμμου
Σχεδόν-κανονικό Ισογώνια Σχεδόν-κανονικό
(διπλή επικάλυψη)

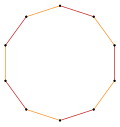t{5} = {10}
t{5/4} = {10/4} = 2{5/2}

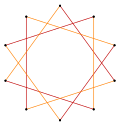t{5/3} = {10/3}
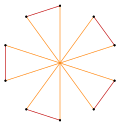
t{5/2} = {10/2} = 2{5}

Εφαρμογές

[Επεξεργασία | επεξεργασία κώδικα]

Τα δεκαγράμματα έχουν χρησιμοποιηθεί ως ένα από τα διακοσμητικά μοτίβα στις πλάκες girih της ισλαμικής αρχιτεκτονικής.[8]

Παραπομπές

[Επεξεργασία | επεξεργασία κώδικα]
  1. ↑ Barnes, John (2012), Gems of Geometry, Springer, σελ. 28–29, ISBN 978-3-6423-0964-9, https://books.google.com/books?id=7YCUBUd-4BQC&pg=PA28 .
  2. ↑ Liddell, Henry George· Scott, Robert. «A Greek-English Lexicon: γραμμή». Perseus. 
  3. ↑ Coxeter, Harold Scott MacDonald (1948). Regular polytopes, p.93-95, regular star polygons, regular star compounds
  4. ↑ Coxeter, Harold Scott MacDonald. (2nd edition), Introduction to Geometry: 2.8 Star polygons, p.36-38
  5. ↑ Branko Grünbaum (1994). The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, Metamorphoses of polygons.
  6. ↑ Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). «Uniform polyhedra». Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences (The Royal Society) 246 (916): 411. doi:10.1098/rsta.1954.0003. ISSN 0080-4614.
    MR 0062446
    .     
  7. ↑ Coxeter, Harold Scott MacDonald. The Densities of the Regular polytopes I, p.43
  8. ↑ Sarhangi, Reza (2012), «Polyhedral Modularity in a Special Class of Decagram Based Interlocking Star Polygons», Bridges 2012: Mathematics, Music, Art, Architecture, Culture, σελ. 165–174, http://archive.bridgesmathart.org/2012/bridges2012-165.pdf .

Εξωτερικοί σύνδεσμοι

[Επεξεργασία | επεξεργασία κώδικα]