Παιχνίδι του Χάους

Δημιουργία ενός τριγώνου Σιερπίνσκι με τη μέθοδο των παιχνιδιών χάους σε κινούμενη εικόνα

Ο τρόπος με τον οποίο λειτουργεί το "παιχνίδι του χάους" απεικονίζεται καλά όταν λαμβάνεται υπ' όψιν κάθε μονοπάτι.

Στα μαθηματικά, ο όρος παιχνίδι του χάους αναφερόταν αρχικά σε μια μέθοδο δημιουργίας ενός φράκταλ, χρησιμοποιώντας ένα πολύγωνο και ένα αρχικό σημείο που επιλέγεται τυχαία στο εσωτερικό του^[1][2]. Το φράκταλ δημιουργείται με την επαναληπτική δημιουργία μιας ακολουθίας σημείων, ξεκινώντας από το αρχικό τυχαίο σημείο, όπου κάθε σημείο στην ακολουθία είναι ένα δεδομένο κλάσμα της απόστασης μεταξύ του προηγούμενου σημείου και μιας από τις κορυφές του πολυγώνου- η κορυφή επιλέγεται τυχαία σε κάθε επανάληψη. Επαναλαμβάνοντας αυτή την επαναληπτική διαδικασία πολλές φορές, επιλέγοντας την κορυφή τυχαία σε κάθε επανάληψη και απορρίπτοντας τα πρώτα σημεία της ακολουθίας, συχνά (αλλά όχι πάντα) θα προκύψει ένα σχήμα φράκταλ. Χρησιμοποιώντας ένα κανονικό τρίγωνο και τον παράγοντα 1/2 θα προκύψει το τρίγωνο Σιερπίνσκι, ενώ η δημιουργία της κατάλληλης διάταξης με τέσσερα σημεία και τον παράγοντα 1/2 θα δημιουργήσει την απεικόνιση ενός "Τετραέδρου Σιερπίνσκι", του τρισδιάστατου αναλόγου του τριγώνου Σιερπίνσκι. Καθώς ο αριθμός των σημείων αυξάνεται σε έναν αριθμό Ν, η διάταξη σχηματίζει ένα αντίστοιχο (Ν-1)-διάστατο Σιερπίνσκι Simplex.

Ο όρος γενικεύτηκε για να αναφερθεί σε μια μέθοδο παραγωγής του ελκυστή ή του σταθερού σημείου οποιουδήποτε συστήματος επαναλαμβανόμενων συναρτήσεων (IFS). Ξεκινώντας με οποιοδήποτε σημείο x0, διαδοχικές επαναλήψεις σχηματίζονται x_k+1 = f_r(x_k), όπου f_r είναι ένα μέλος του συγκεκριμένου IFS που επιλέγεται τυχαία για κάθε επανάληψη. Οι επαναλήψεις συγκλίνουν στο σταθερό σημείο του IFS. Όποτε το x₀ ανήκει στον ελκυστή του IFS, όλες οι επαναλήψεις x_k παραμένουν εντός του ελκυστή και, με πιθανότητα 1, σχηματίζουν ένα πυκνό σύνολο σε αυτόν.

Η μέθοδος του " παιχνιδιού του χάους " απεικονίζει σημεία με τυχαία σειρά σε όλο τον ελκυστή. Αυτό έρχεται σε αντίθεση με άλλες μεθόδους σχεδίασης φράκταλ, οι οποίες ελέγχουν κάθε εικονοστοιχείο στην οθόνη για να δουν αν ανήκει στο φράκταλ. Το γενικό σχήμα ενός φράκταλ μπορεί να σχεδιαστεί γρήγορα με τη μέθοδο " παιχνίδι του χάους ", αλλά μπορεί να είναι δύσκολο να σχεδιαστεί λεπτομερώς ορισμένες περιοχές του φράκταλ.

Με τη βοήθεια του "παιχνιδιού του χάους" μπορεί να δημιουργηθεί ένα νέο φράκταλ και κατά τη δημιουργία του νέου φράκταλ μπορούν να ληφθούν ορισμένες παράμετροι. Αυτές οι παράμετροι είναι χρήσιμες για εφαρμογές της μορφοκλασματικής θεωρίας, όπως η ταξινόμηση και η ταυτοποίηση.^[3][4] Το νέο φράκταλ είναι αυτο-ομοειδές με το αρχικό σε ορισμένα σημαντικά χαρακτηριστικά, όπως η διάσταση φράκταλ.

Περιορισμένο παιχνίδι του χάους

Ένα σημείο μέσα σε ένα τετράγωνο μετακινείται επανειλημμένα κατά το ήμισυ της απόστασης προς μια τυχαία επιλεγμένη κορυφή. Δεν εμφανίζεται κανένα φράκταλ.

Αν το παιχνίδι του χάους διεξάγεται με ένα τετράγωνο, δεν εμφανίζεται κανένα φράκταλ και το εσωτερικό του τετραγώνου γεμίζει ομοιόμορφα με σημεία. Εντούτοις, εάν τεθούν περιορισμοί στην επιλογή των κορυφών, θα εμφανιστούν φράκταλ στο τετράγωνο. Για παράδειγμα, εάν η τρέχουσα κορυφή δεν μπορεί να επιλεγεί στην επόμενη επανάληψη, εμφανίζεται αυτό το φράκταλ:

Ένα σημείο μέσα σε ένα τετράγωνο μετακινείται επανειλημμένα κατά το ήμισυ της απόστασης προς μια τυχαία επιλεγμένη κορυφή, ωστόσο η τρέχουσα επιλεγμένη κορυφή δεν μπορεί να είναι η ίδια με την προηγούμενη επιλεγμένη κορυφή.

Εάν η τρέχουσα κορυφή δεν μπορεί να μετακινηθεί μία θέση (αριστερόστροφα) μακριά από την προηγουμένως επιλεγμένη κορυφή, τότε εμφανίζεται το συγκεκριμένο φράκταλ:

Ένα σημείο μέσα σε ένα τετράγωνο μετακινείται επανειλημμένα κατά το ήμισυ της αποστάσεως προς μια τυχαία επιλεγμένη κορυφή, αλλά η τρέχουσα επιλεγμένη κορυφή δεν μπορεί να απέχει 1 θέση αριστερόστροφα από την προηγούμενη επιλεγμένη κορυφή.

Εάν το σημείο εμποδίζεται να προσγειωθεί σε μια συγκεκριμένη περιοχή του τετραγώνου, το σχήμα αυτής της περιοχής θα αναπαραχθεί ως φράκταλ σε άλλα και φαινομενικά απεριόριστα μέρη του τετραγώνου.

Άλλοι περιορισμοί δημιουργούν πρόσθετα φράκταλ:

Ένα σημείο μέσα σε ένα τετράγωνο μεταπηδά επανειλημμένα κατά το ήμισυ της αποστάσεως προς μια τυχαία επιλεγμένη κορυφή, αλλά η τρέχουσα επιλεγμένη κορυφή δεν μπορεί να απέχει 2 θέσεις από την προηγούμενη επιλεγμένη κορυφή. Ένα σημείο μέσα σε ένα τετράγωνο μεταπηδά επανειλημμένα κατά το ήμισυ της αποστάσεως προς μια τυχαία επιλεγμένη κορυφή, αλλά η τρέχουσα επιλεγμένη κορυφή δεν μπορεί να απέχει 2 θέσεις από την προηγούμενη επιλεγμένη κορυφή.   Ένα σημείο μέσα σε ένα τετράγωνο μετακινείται διαρκώς κατά το ήμισυ της αποστάσεως προς μια τυχαία επιλεγμένη κορυφή, αλλά η τρέχουσα επιλεγμένη κορυφή δεν μπορεί να γειτνιάσει με την προηγουμένως επιλεγμένη κορυφή, εάν οι δύο προηγουμένως επιλεγμένες κορυφές είναι ίδιες. Ένα σημείο μέσα σε ένα τετράγωνο μετακινείται διαρκώς κατά το ήμισυ της αποστάσεως προς μια τυχαία επιλεγμένη κορυφή, αλλά η τρέχουσα επιλεγμένη κορυφή δεν μπορεί να γειτνιάσει με την προηγουμένως επιλεγμένη κορυφή, εάν οι δύο προηγουμένως επιλεγμένες κορυφές είναι ίδιες.   Ένα σημείο μέσα σε ένα πεντάγωνο μετακινείται συνεχώς κατά το ήμισυ της απόστασης προς μια τυχαία επιλεγμένη κορυφή, αλλά η τρέχουσα επιλεγμένη κορυφή δεν μπορεί να είναι η ίδια με την προηγούμενη επιλεγμένη κορυφή. Ένα σημείο μέσα σε ένα πεντάγωνο μετακινείται συνεχώς κατά το ήμισυ της απόστασης προς μια τυχαία επιλεγμένη κορυφή, αλλά η τρέχουσα επιλεγμένη κορυφή δεν μπορεί να είναι η ίδια με την προηγούμενη επιλεγμένη κορυφή.   Ένα σημείο μέσα σε ένα πεντάγωνο μετακινείται διαρκώς κατά το ήμισυ της απόστασης προς μια τυχαία επιλεγμένη κορυφή, αλλά η τρέχουσα επιλεγμένη κορυφή δεν μπορεί να γειτνιάσει με την προηγουμένως επιλεγμένη κορυφή, εάν οι δύο προηγουμένως επιλεγμένες κορυφές είναι ίδιες. Ένα σημείο μέσα σε ένα πεντάγωνο μετακινείται διαρκώς κατά το ήμισυ της απόστασης προς μια τυχαία επιλεγμένη κορυφή, αλλά η τρέχουσα επιλεγμένη κορυφή δεν μπορεί να γειτνιάσει με την προηγουμένως επιλεγμένη κορυφή, εάν οι δύο προηγουμένως επιλεγμένες κορυφές είναι ίδιες.

Άλματα εκτός του 1/2

Όταν το μήκος του άλματος προς μια κορυφή ή ένα άλλο σημείο δεν είναι 1/2, το παιχνίδι του χάους παράγει άλλα φράκταλ, μερικά από τα οποία είναι πολύ γνωστά. Για παράδειγμα, όταν το άλμα είναι 2/3 και το σημείο μπορεί επίσης να μεταβεί προς το κέντρο του τετραγώνου, το παίγνιο χάους παράγει το φράκταλ Vicsek:

Ένα φράκταλ Vicsek που παράγεται από το παιχνίδι του χάους

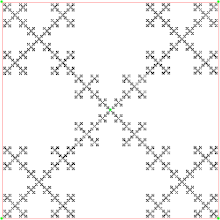
Όταν το άλμα είναι 2/3 και το σημείο μπορεί επίσης να μεταπηδήσει προς τα μέσα των τεσσάρων πλευρών, το παίγνιο χάους δημιουργεί το χαλί Σιερπίνσκι:

Ένα χαλί του Σιερπίνσκι που παράγεται από το παιχνίδι χάους

Όταν το άλμα είναι 1/φ και το σημείο κινείται τυχαία προς τη μία ή την άλλη από τις πέντε κορυφές ενός κανονικού πενταγώνου, το παιχνίδι του χάους παράγει ένα πενταγωνικό n-νιφάδα:

Μια πενταγωνική n-νιφάδα παράγεται από το παιχνίδι του χάους

Δείτε επίσης

• Αναδρομή
• Σύνολο Μάντελμπροτ
• Σύνολο Julia
• Οικοδομήσιμο Σύμπαν

βιβλιογραφία

• Warren Jr., Henry S. (2013). Hacker's Delight (2 έκδοση). Addison Wesley – Pearson Education, Inc. ISBN 978-0-321-84268-8. 
• McKenna, Douglas M. (2019). Hilbert Curves: Outside-In and Inside-Gone. Mathemaesthetics, Inc. ISBN 978-1-7332188-0-1. 

Παραπομπές

1. Weisstein, Eric W., "Chaos Game" από το MathWorld.
2. Barnsley, Michael (1993). Fractals Everywhere. Morgan Kaufmann. ISBN 978-0-12-079061-6. 
3. Jampour, Mahdi; Yaghoobi, Mahdi; Ashourzadeh, Maryam; Soleimani, Adel (1 September 2010). «A new fast technique for fingerprint identification with fractal and chaos game theory» (στα αγγλικά). Fractals 18 (3): 293–300. doi:10.1142/s0218348x10005020. ISSN 0218-348X. https://www.researchgate.net/publication/243541547. 
4. Jampour, Mahdi; Javidi, Mohammad M.; Soleymani, Adel; Ashourzadeh, Maryam; Yaghoobi, Mahdi (2010). «A New Technique in saving Fingerprint with low volume by using Chaos Game and Fractal Theory» (στα αγγλικά). International Journal of Interactive Multimedia and Artificial Intelligence 1 (3): 27. doi:10.9781/ijimai.2010.135. ISSN 1989-1660.