Παράδοξο Φάραντεϊ

Βούρτσα βούρτσα, στατικό μαγνητικό πεδίο B, περιστροφή ω, η εφαπτομενική συνιστώσα του v, δύναμη Lorentz v × B

Όταν ο δίσκος αλουμινίου περιστρέφεται, το βολτόμετρο λαμβάνει τάση. Αν, από την άλλη πλευρά, περιστρέφεται μόνο ο μαγνήτης, η ένδειξη τάσης παραμένει μηδενική. Εάν περιστραφούν τόσο ο μαγνήτης όσο και ο δίσκος αλουμινίου, μπορεί να μετρηθεί μια τάση.

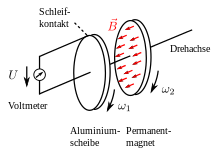
Το παράδοξο του Φάραντεϊ είναι πείραμα που περιγράφηκε για πρώτη φορά από τον Μάικλ Φαραντέι, το οποίο με την πρώτη ματιά φαίνεται να αντιφάσκει με τον νόμο της επαγωγής του.

Η πειραματική διάταξη αποτελείται από έναν κυλινδρικό μόνιμο μαγνήτη και έναν παρακείμενο αγώγιμο δίσκο, οι οποίοι είναι τοποθετημένοι έτσι ώστε να περιστρέφονται γύρω από έναν άξονα. Ο άξονας συμμετρίας του μαγνήτη και του δίσκου συμπίπτει με τον άξονα περιστροφής και ο μαγνήτης έχει την πόλωσή του στην αξονική κατεύθυνση (δηλαδή οι πόλοι βρίσκονται στον άξονα). Η ηλεκτρική τάση μετράται στο δίσκο μεταξύ του άξονα και της άκρης του- για το σκοπό αυτό, τοποθετούνται ολισθαίνουσες επαφές στο εξωτερικό του και κοντά στον άξονα.

Εάν ο δίσκος περιστραφεί ενώ ο μαγνήτης είναι σε ηρεμία, παράγεται τάση στους ακροδέκτες. Αυτό μπορεί να περιγραφεί με τη δύναμη Lorentz ή τον κανόνα της ροής (μονοπολική επαγωγή). Η τελική τάση εμφανίζεται επίσης όταν ο δίσκος και ο μαγνήτης συνδέονται μηχανικά και μετακινούνται μαζί. Αν, από την άλλη πλευρά, μόνο ο μαγνήτης κινείται και ο δίσκος είναι σε ηρεμία, δεν εμφανίζεται καμία τάση στον ακροδέκτη. Αυτό προβλημάτισε τον Φαραντέι, επειδή υπέθεσε ότι το μόνο που είχε σημασία για την εμφάνιση της τάσης ήταν ότι ο δίσκος κινούνταν ενάντια στον μαγνήτη.

Στην πραγματικότητα, όμως, το μαγνητικό πεδίο του μόνιμου μαγνήτη είναι (σε μεγάλο βαθμό) ανεξάρτητο από την περιστροφή του. Επομένως, δεν έχει καμία διαφορά αν περιστρέφεται ή όχι. Από την άλλη πλευρά, (για έναν παρατηρητή σε ηρεμία) η δύναμη Lorentz δρα στα ηλεκτρόνια του δίσκου μόλις αυτά μετακινηθούν μέσα στο μαγνητικό πεδίο. Επομένως, μετράται μια τάση μεταξύ των σταθερών επαφών ολίσθησης ακριβώς όταν ο δίσκος περιστρέφεται.

Αν εξετάσουμε το πείραμα όχι από τη σκοπιά του παρατηρητή σε ηρεμία, αλλά ως παρατηρητής που κινείται μαζί με το δίσκο (περιστρεφόμενος γύρω από τον άξονα), θα μετράμε πάντα μηδενική τάση μεταξύ του κέντρου και της άκρης του δίσκου- το μαγνητικό πεδίο είναι ανεξάρτητο από οποιαδήποτε περιστροφή του μαγνήτη. Από την άλλη πλευρά, μια επαγωγική τάση θα μετρηθεί στο κύκλωμα μεταξύ των (για τον συγκεκριμένο παρατηρητή) περιστρεφόμενων επαφών ολίσθησης, επειδή το κύκλωμα αυτό είναι ένας αγωγός που περιστρέφεται στο μαγνητικό πεδίο.

Αυτό το φαινόμενο, το οποίο δεν είναι εύκολο να κατανοηθεί, οδήγησε ξανά και ξανά σε παρεξηγήσεις και έτσι, για παράδειγμα, σε διάφορες προσπάθειες να κατασκευαστεί ένα είδος μηχανής αέναης κίνησης, η λεγόμενη μηχανή Ν, με βάση τη μονοπολική επαγωγή.

Σημειώσεις

Άλλα

• Michael Faraday, Experimental Researches in Electricity, Vol I, First Series, 1831 in Great Books of the Western World, Vol 45, R. M. Hutchins, ed., Encyclopædia Britannica, Inc., The University of Chicago, 1952. [1]
• "Electromagnetic induction: physics and flashbacks" (PDF) Αρχειοθετήθηκε 2018-02-19 στο Wayback Machine. by Giuseppe Giuliani – details of the Lorentz force in Faraday's disc
• "Homopolar Electric Dynamo" – contains derivation of equation for EMF of a Faraday disc
• Don Lancaster's "Tech Musings" column, Feb 1998 – on practical inefficiencies of Faraday disc
• "Faraday's Final Riddle; Does the Field Rotate with a Magnet?" (PDF) – contrarian theory, but contains useful references to Faraday's experiments
• P. J. Scanlon, R. N. Henriksen, and J. R. Allen, "Approaches to electromagnetic induction," Am. J. Phys. 37, 698–708 (1969). – describes how to apply Faraday's law to Faraday's disc
• Jorge Guala-Valverde, Pedro Mazzoni, Ricardo Achilles "The homopolar motor: A true relativistic engine," Am. J. Phys. 70 (10), 1052–1055 (Oct. 2002). – argues that only the Lorentz force can explain Faraday's disc and describes some experimental evidence for this
• Frank Munley, Challenges to Faraday's flux rule, Am. J. Phys. 72, 1478 (2004). – an updated discussion of concepts in the Scanlon reference above.
• Richard Feynman, Robert Leighton, Matthew Sands, "The Feynman Lectures on Physics Volume II", Chapter 17 – In addition to the Faraday "paradox" (where linked flux does not change but an emf is induced), he describes the "rocking plates" experiment where linked flux changes but no emf is induced. He shows that the correct physics is always given by the combination of the Lorentz force with the Maxwell–Faraday equation (see quotation box) and poses these two "paradoxes" of his own.
• The rotation of magnetic field by Vanja Janezic – describes a simple experiment that anyone can do. Because it only involves two bodies, its result is less ambiguous than the three-body Faraday, Kelly and Guala-Valverde experiments.
• W. F. Hughes and F. J. Young, The Electromagnetodynamics of Fluids, John Wiley & Sons (1965) LCCC #66-17631. Chapters 1. Principles of Special Relativity and 2. The Electrodynamics of Moving Media. From these chapters it is possible to work all induced emf problems and explain all the associated paradoxes found in the literature.