Penrosa kahelaro

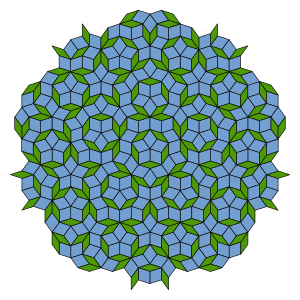
Penrosa kahelaro estas senperioda kahelaro, kiun naskas senperioda aro de prakaheloj.^[1] Penrosaj kahelaroj nomiĝas laŭ matematikisto kaj fizikisto Roger PENROSE, kiu esploris tiujn arojn dum la 1970-aj jaroj. La senperiodeco de la penrosaj prakaheloj implicas ke ŝoviĝita kopio de penrosa kahelaro neniam kongruas kun la originalo. Oni povas konstrui penrosan kahelaron tiel ke ĝi prezentas kaj reflektan simetrion kaj kvinoblan turnan simetrion.

Penrosa kahelaro havas multajn rimarkindajn trajtojn, plej precipe:

Ĝi ne periodas, kiu signifas ke ĝi mankas ajna translacia simetrio.
Ĝi memsimilas, tiel ke la samaj patroneoj okazas ĉe pli kaj pli grandaj skaloj. Tiel, la kahelaro estas atingebla tra "inflacio" aŭ "deflacio" (dilati aŭ redukti de la prakaheloj, kiun nomiĝas anstataŭa kahelaro), kaj ĉiu ajn finhava peceto de la kahelaro okazas senlime multajn fojojn.
Ĝi estas kvazaŭkristalo: kiel fizika strukturo, penrosa kahelaro produktos Bragg-difrakton, kaj ĝian difraktogram montras kaj la kvinoblan simetrion kaj la subkuŝan longdistancan ordon.

Diversaj metodoj por konstrui penrosajn kahelarojn estas malkovritaj, inkluzive de reguloj pri kongrueco, anstataŭa kahelaro, tranĉi- kaj projekci-skemoj kaj kovraĵoj.

Historio

Periodaj kaj senperiodaj kahelaroj

"Dudimensia patronea montras regulan, ripetitan arojn de bluaj kaj verdaj romboj. La izometra desegno povas doni la aspekton de multaj kuboj, ĉiu kun du alfronte bluaj facoj kaj unu supre verda faco." — Parto de regula, perioda kahelaro

Penrosaj kahelaroj estas simplaj ekzemploj de senperiodaj kahelaroj de la ebeno. Kahelaro kovras la ebenon per kaheloj kun neniuj superkuŝoj aŭ manklokoj; la kaheloj normale havas finhavan nombron da formoj, nomitaj prakaheloj, kaj oni diras, ke aro de prakaheloj allasas kahelaron aŭ kahelas la ebenon se ekzistas ebenkahelaro uzante nur kahelojn kiuj kongruas kun ĉi tiuj prakaheloj.^[2] La plej konataj kahelaroj (ekzemple, per kvaranguloj aŭ trianguloj) periodas: perfekta kopio de la kahelaro deriviĝas per translacio de ĉiuj kaheloj tra fiksa distanco en antaŭfiksita direkto. Tia translacio nomiĝas periodo de la kahelaro; pli neformale, tio signifas, ke finhava regiono de la kahelaro ripetas sin laŭ periodaj intervaloj. Se kahelaro havas neniujn periodojn, ĝi laŭdire estas neperioda. Aro de prakaheloj laŭdire estas senperioda se ĝi kahelas la ebenon sed ĉiu tia kahelaro ne periodas; kahelaroj de senperiodaj aroj de prakaheloj nomiĝas senperiodaj kahelaroj.^[3]

Penrosaj kahelaroj kun oraj trianguloj

Referencoj

↑ Ĝeneralaj referencoj por ĉi tiu artikolo inkluzivas Martin GARDNER, Penrose Tiles to Trapdoor Ciphers ("Penrosaj kaheloj al klappordaj ĉifroj"), 1997, Cambridge Univ. Press, paĝoj 1–30, ISBN 978-0-88385-521-8; Branko GRÜNBAUM kaj G. C. SHEPHARD, Tilings and Patterns ("Kahelaroj kaj patroneoj"), 1987, New York: W. H. Freeman, paĝoj 520–548, ISBN 0-7167-1193-1; kaj Marjorie SENECHAL, Quasicrystals and geometry ("Kvazaŭkristaloj kaj geometrio") 1996, Cambridge Univ. Press, paĝoj 170–206, ISBN 978-0-521-57541-6.
↑ Gardner, op. cit., 1997, paĝoj 20, 23
↑ Grünbaum kaj Shephard, op. cit., paĝo 520

Penrosa kahelaro en la Vikimedia Komunejo (Multrimedaj datumoj)
Kategorio Penrosa kahelaro en la Vikimedia Komunejo (Multrimedaj datumoj)

[enkonduko-1] Ĝeneralaj referencoj por ĉi tiu artikolo inkluzivas Martin GARDNER, Penrose Tiles to Trapdoor Ciphers ("Penrosaj kaheloj al klappordaj ĉifroj"), 1997, Cambridge Univ. Press, paĝoj 1–30, ISBN 978-0-88385-521-8; Branko GRÜNBAUM kaj G. C. SHEPHARD, Tilings and Patterns ("Kahelaroj kaj patroneoj"), 1987, New York: W. H. Freeman, paĝoj 520–548, ISBN 0-7167-1193-1; kaj Marjorie SENECHAL, Quasicrystals and geometry ("Kvazaŭkristaloj kaj geometrio") 1996, Cambridge Univ. Press, paĝoj 170–206, ISBN 978-0-521-57541-6.

[Gard20-2] Gardner, op. cit., 1997, paĝoj 20, 23

[Shep520-3] Grünbaum kaj Shephard, op. cit., paĝo 520

[1]

[2]

[3]