| Kombinaĵo
|
Simbolo
|
Bildo
|
Kvanto de pluredroj
|
Pluredroj
|
Edroj
|
Lateroj
|
Verticoj
|
Notoj
|
Geometria simetria grupo
|
Subgrupo limigita al unu komponanto
|
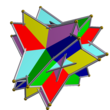
| Kombinaĵo de 6 kvaredroj kun turna libereco
|
UC01
|
|
6
|
Kvaredroj
|
24{3}
|
36
|
24
|
Turna libereco
|
Kvaredra simetrio Td
|
Cikla simetrio S4
|
| Kombinaĵo de 12 kvaredroj kun turna libereco
|
UC02
|

|
12
|
Kvaredroj
|
48{3}
|
72
|
48
|
Turna libereco
|
Okedra simetrio Oh
|
Cikla simetrio S4
|
| Kombinaĵo de 6 kvaredroj
|
UC03
|

|
6
|
Kvaredroj
|
24{3}
|
36
|
24
|
|
Okedra simetrio Oh
|
Duedra simetrio en tri dimensioj D2d
|
| Kombinaĵo de 2 kvaredroj
|
UC04
|

|
2
|
Kvaredroj
|
8{3}
|
12
|
8
|
Regula
|
Okedra simetrio Oh
|
Kvaredra simetrio Td
|
| Kombinaĵo de 5 kvaredroj
|
UC05
|

|
5
|
Kvaredroj
|
20{3}
|
30
|
20
|
Regula
|
Dudekedra simetrio I
|
Kvaredra simetrio T
|
| Kombinaĵo de 10 kvaredroj
|
UC06
|

|
10
|
Kvaredroj
|
40{3}
|
60
|
20
|
Regula
2 komponantaj pluredroj koincidas je ĉiu vertico
|
Dudekedra simetrio Ih
|
Kvaredra simetrio T
|
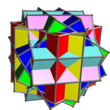
| Kombinaĵo de 6 kuboj kun turna libereco
|
UC07
|
|
6
|
Kuboj
|
(12+24){4}
|
72
|
48
|
Turna libereco
|
Okedra simetrio Oh
|
Cikla simetrio C4h
|
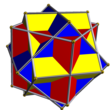
| Kombinaĵo de 3 kuboj
|
UC08
|
|
3
|
Kuboj
|
(6+12){4}
|
36
|
24
|
|
Okedra simetrio Oh
|
Duedra simetrio D4h
|
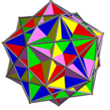
| Kombinaĵo de 5 kuboj
|
UC09
|
|
5
|
Kuboj
|
30{4}
|
60
|
20
|
Regula
2 komponantaj pluredroj koincidas je ĉiu vertico
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 4 okedroj kun turna libereco
|
UC10
|

|
4
|
Okedroj
|
(8+24){3}
|
48
|
24
|
Turna libereco
|
Kvaredra simetrio Th
|
Cikla simetrio S6
|
| Kombinaĵo de 8 okedroj kun turna libereco
|
UC11
|

|
8
|
Okedroj
|
(16+48){3}
|
96
|
48
|
Turna libereco
|
Okedra simetrio Oh
|
Cikla simetrio S6
|
| Kombinaĵo de 4 okedroj
|
UC12
|

|
4
|
Okedroj
|
(8+24){3}
|
48
|
24
|
|
Okedra simetrio Oh
|
Duedra simetrio D3d
|
| Kombinaĵo de 20 okedroj kun turna libereco
|
UC13
|

|
20
|
Okedroj
|
(40+120){3}
|
240
|
120
|
Turna libereco
|
Dudekedra simetrio Ih
|
Cikla simetrio S6
|
| Kombinaĵo de 20 okedroj
|
UC14
|

|
20
|
Okedroj
|
(40+120){3}
|
240
|
60
|
2 komponantaj pluredroj koincidas je ĉiu vertico
|
Dudekedra simetrio Ih
|
Cikla simetrio S6
|
| Kombinaĵo de 10 okedroj
|
UC15
|

|
10
|
Okedroj
|
(20+60){3}
|
120
|
60
|
|
Dudekedra simetrio Ih
|
Duedra simetrio D3d
|
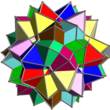
| Kombinaĵo de 10 okedroj
|
UC16
|
|
10
|
Okedroj
|
(20+60){3}
|
120
|
60
|
|
Dudekedra simetrio Ih
|
Duedra simetrio D3d
|
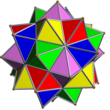
| Kombinaĵo de 5 okedroj
|
UC17
|
|
5
|
Okedroj
|
40{3}
|
60
|
30
|
Regula
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 5 kvar-duon-sesedroj
|
UC18
|

|
5
|
Kvar-duon-sesedroj
|
20{3}
15{4}
|
60
|
30
|
|
Dudekedra simetrio I
|
Kvaredra simetrio T
|
| Kombinaĵo de 20 kvar-duon-sesedroj
|
UC19
|

|
20
|
Kvar-duon-sesedroj
|
(20+60){3}
60{4}
|
240
|
60
|
2 komponantaj pluredroj koincidas je ĉiu vertico
|
Dudekedra simetrio I
|
Cikla simetrio C3
|
| Prisma kombinaĵo de prismoj kun turna libereco
|
UC20
|

|
2n
(n>0)
|
p/q-lateraj prismoj
|
4n{p/q}
2np{4}
|
6np
|
4np
|
Turna libereco
PGKD(p,q)=1, p/q>2
|
Duedra simetrio D(np)h
|
Cikla simetrio Cph
|
| Prisma kombinaĵo de prismoj
|
UC21
|

|
n
(n>1)
|
p/q-lateraj prismoj
|
2n{p/q}
np{4}
|
3np
|
2np
|
PGKD(p,q)=1, p/q>2
|
Duedra simetrio D(np)h
|
Duedra simetrio Dph
|
| Prisma kombinaĵo de kontraŭprismoj kun turna libereco
|
UC22
|

|
2n
(n>0)
|
p/q-lateraj kontraŭprismoj (kvaredroj se p/q=2)
(q nepara)
|
4n{p/q} (se ne p/q=2)
4np{3}
|
8np
|
4np
|
Turna libereco
PGKD(p,q)=1, p/q>3/2
|
Duedra simetrio D(np)d (se n nepara)
Duedra simetrio D(np)h (se n para)
|
Cikla simetrio S2p
|
| Prisma kombinaĵo de kontraŭprismoj
|
UC23
|

|
n
(n>1)
|
p/q-lateraj kontraŭprismoj (kvaredroj se p/q=2)
(q nepara)
|
2n{p/q} (se ne p/q=2)
2np{3}
|
4np
|
2np
|
PGKD(p,q)=1, p/q>3/2
|
Duedra simetrio D(np)d (se n nepara)
Duedra simetrio D(np)h (se n para)
|
Duedra simetrio Dpd
|
| Prisma kombinaĵo de kontraŭprismoj kun turna libereco
|
UC24
|

|
2n
(n>0)
|
p/q-lateraj kontraŭprismoj
(q para)
|
4n{p/q}
4np{3}
|
8np
|
4np
|
Turna libereco
PGKD(p,q)=1, p/q>3/2
|
Duedra simetrio D(np)h
|
Cikla simetrio Cph
|
| Prisma kombinaĵo de kontraŭprismoj
|
UC25
|

|
n
(n>1)
|
p/q-lateraj kontraŭprismoj
(q para)
|
2n{p/q}
2np{3}
|
4np
|
2np
|
PGKD(p,q)=1, p/q>3/2
|
Duedra simetrio D(np)h
|
Duedra simetrio Dph
|
| Kombinaĵo de 12 kvinlateraj kontraŭprismoj kun turna libereco
|
UC26
|

|
12
|
Kvinlateraj kontraŭprismoj
|
120{3}
24{5}
|
240
|
120
|
Turna libereco
|
Dudekedra simetrio Ih
|
Cikla simetrio S10
|
| Kombinaĵo de 6 kvinlateraj kontraŭprismoj
|
UC27
|

|
6
|
Kvinlateraj kontraŭprismoj
|
60{3}
12{5}
|
120
|
60
|
|
Dudekedra simetrio Ih
|
Duedra simetrio D5d
|
| Kombinaĵo de 12 stelokvinlateraj krucigitaj kontraŭprismoj kun turna libereco
|
UC28
|

|
12
|
Stelokvinlateraj krucigitaj kontraŭprismoj
|
120{3}
24{5/2}
|
240
|
120
|
Turna libereco
|
Dudekedra simetrio Ih
|
Cikla simetrio S10
|
| Kombinaĵo de 6 stelokvinlateraj krucigitaj kontraŭprismoj
|
UC29
|

|
6
|
Stelokvinlateraj krucigitaj kontraŭprismoj
|
60{3}
12{5/2}
|
120
|
60
|
|
Dudekedra simetrio Ih
|
Duedra simetrio D5d
|
| Kombinaĵo de 4 triangulaj prismoj
|
UC30
|

|
4
|
Triangulaj prismoj
|
8{3}
12{4}
|
36
|
24
|
|
Okedra simetrio O
|
Duedra simetrio D3
|
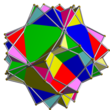
| Kombinaĵo de 8 triangulaj prismoj
|
UC31
|
|
8
|
Triangulaj prismoj
|
16{3}
24{4}
|
72
|
48
|
|
Okedra simetrio Oh
|
Duedra simetrio D3
|
| Kombinaĵo de 10 triangulaj prismoj
|
UC32
|

|
10
|
Triangulaj prismoj
|
20{3}
30{4}
|
90
|
60
|
|
Dudekedra simetrio I
|
Duedra simetrio D3
|
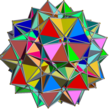
| Kombinaĵo de 20 triangulaj prismoj
|
UC33
|
|
20
|
Triangulaj prismoj
|
40{3}
60{4}
|
180
|
60
|
2 komponantaj pluredroj koincidas je ĉiu vertico
|
Dudekedra simetrio Ih
|
Duedra simetrio D3
|
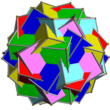
| Kombinaĵo de 6 kvinlateraj prismoj
|
UC34
|
|
6
|
Kvinlateraj prismoj
|
30{4}
12{5}
|
90
|
60
|
|
Dudekedra simetrio I
|
Duedra simetrio D5
|
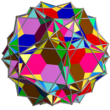
| Kombinaĵo de 12 kvinlateraj prismoj
|
UC35
|
|
12
|
Kvinlateraj prismoj
|
60{4}
24{5}
|
180
|
60
|
2 komponantaj pluredroj koincidas je ĉiu vertico
|
Dudekedra simetrio Ih
|
Duedra simetrio D5
|
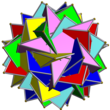
| Kombinaĵo de 6 stelokvinlateraj prismoj
|
UC36
|
|
6
|
Stelokvinlateraj prismoj
|
30{4}
12{5/2}
|
90
|
60
|
|
Dudekedra simetrio I
|
Duedra simetrio D5
|
| Kombinaĵo de 12 stelokvinlateraj prismoj
|
UC37
|

|
12
|
Stelokvinlateraj prismoj
|
60{4}
24{5/2}
|
180
|
60
|
2 komponantaj pluredroj koincidas je ĉiu vertico
|
Dudekedra simetrio Ih
|
Duedra simetrio D5
|
| Kombinaĵo de 4 seslateraj prismoj
|
UC38
|

|
4
|
Seslateraj prismoj
|
24{4}
8{6}
|
72
|
48
|
|
Okedra simetrio Oh
|
Duedra simetrio D3d
|
| Kombinaĵo de 10 seslateraj prismoj
|
UC39
|

|
10
|
Seslateraj prismoj
|
60{4}
20{6}
|
180
|
120
|
|
Dudekedra simetrio Ih
|
Duedra simetrio D3d
|
| Kombinaĵo de 6 deklateraj prismoj
|
UC40
|

|
6
|
Deklateraj prismoj
|
60{4}
12{10}
|
180
|
120
|
|
Dudekedra simetrio Ih
|
Duedra simetrio D5d
|
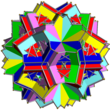
| Kombinaĵo de 6 stelodeklateraj prismoj
|
UC41
|
|
6
|
Stelodeklateraj prismoj
|
60{4}
12{10/3}
|
180
|
120
|
|
Dudekedra simetrio Ih
|
Duedra simetrio D5d
|
| Kombinaĵo de 3 kvadrataj kontraŭprismoj
|
UC42
|

|
3
|
Kvadrataj kontraŭprismoj
|
24{3}
6{4}
|
48
|
24
|
|
Okedra simetrio O
|
Duedra simetrio D4
|
| Kombinaĵo de 6 kvadrataj kontraŭprismoj
|
UC43
|

|
6
|
Kvadrataj kontraŭprismoj
|
48{3}
12{4}
|
96
|
48
|
|
Okedra simetrio Oh
|
Duedra simetrio D4
|
| Kombinaĵo de 6 stelokvinlateraj kontraŭprismoj
|
UC44
|

|
6
|
Stelokvinlateraj kontraŭprismoj
|
60{3}
12{5/2}
|
120
|
60
|
|
Dudekedra simetrio I
|
Duedra simetrio D5
|
| Kombinaĵo de 12 stelokvinlateraj kontraŭprismoj
|
UC45
|

|
12
|
Stelokvinlateraj kontraŭprismoj
|
120{3}
24{5/2}
|
240
|
120
|
|
Dudekedra simetrio Ih
|
Duedra simetrio D5
|
| Kombinaĵo de 2 dudekedroj
|
UC46
|

|
2
|
Dudekedroj
|
(16+24){3}
|
60
|
24
|
|
Okedra simetrio Oh
|
Kvaredra simetrio Th
|
| Kombinaĵo de 5 dudekedroj
|
UC47
|

|
5
|
Dudekedroj
|
(40+60){3}
|
150
|
60
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 2 grandaj dekduedroj
|
UC48
|

|
2
|
Grandaj dekduedroj
|
24{5}
|
60
|
24
|
|
Okedra simetrio Oh
|
Kvaredra simetrio Th
|
| Kombinaĵo de 5 grandaj dekduedroj
|
UC49
|

|
5
|
Grandaj dekduedroj
|
60{5}
|
150
|
60
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 2 malgrandaj steligitaj dekduedroj
|
UC50
|

|
2
|
Malgrandaj steligitaj dekduedroj
|
24{5/2}
|
60
|
24
|
|
Okedra simetrio Oh
|
Kvaredra simetrio Th
|
| Kombinaĵo de 5 malgrandaj steligitaj dekduedroj
|
UC51
|

|
5
|
Malgrandaj steligitaj dekduedroj
|
60{5/2}
|
150
|
60
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 2 grandaj dudekedroj
|
UC52
|

|
2
|
Grandaj dudekedroj
|
(16+24){3}
|
60
|
24
|
|
Okedra simetrio Oh
|
Kvaredra simetrio Th
|
| Kombinaĵo de 5 grandaj dudekedroj
|
UC53
|

|
5
|
Grandaj dudekedroj
|
(40+60){3}
|
150
|
60
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 2 senpintigitaj kvaredroj
|
UC54
|

|
2
|
Senpintigitaj kvaredroj
|
8{3}
8{6}
|
36
|
24
|
|
Okedra simetrio Oh
|
Kvaredra simetrio Td
|
| Kombinaĵo de 5 senpintigitaj kvaredroj
|
UC55
|

|
5
|
Senpintigitaj kvaredroj
|
20{3}
20{6}
|
90
|
60
|
|
Dudekedra simetrio I
|
Kvaredra simetrio T
|
| Kombinaĵo de 10 senpintigitaj kvaredroj
|
UC56
|

|
10
|
Senpintigitaj kvaredroj
|
40{3}
40{6}
|
180
|
120
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio T
|
| Kombinaĵo de 5 senpintigitaj kuboj
|
UC57
|

|
5
|
Senpintigitaj kuboj
|
40{3}
30{8}
|
180
|
120
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 5 steligitaj senpintigitaj kuboj
|
UC58
|

|
5
|
Steligitaj senpintigitaj kuboj
|
40{3}
30{8/3}
|
180
|
120
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 5 kubokedroj
|
UC59
|

|
5
|
Kubokedroj
|
40{3}
30{4}
|
120
|
60
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 5 kubo-duon-okedroj
|
UC60
|

|
5
|
Kubo-duon-okedroj
|
30{4}
20{6}
|
120
|
60
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 5 ok-duon-okedroj
|
UC61
|

|
5
|
Ok-duon-okedroj
|
40{3}
20{6}
|
120
|
60
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 5 malgrandaj rombokub-okedroj
|
UC62
|

|
5
|
Malgrandaj rombokub-okedroj
|
40{3}
(30+60){4}
|
240
|
120
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 5 malgrandaj rombo-sesedroj
|
UC63
|

|
5
|
Malgrandaj rombo-sesedroj
|
60{4}
30{8}
|
240
|
120
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 5 malgrandaj kubokubo-okedroj
|
UC64
|

|
5
|
Malgrandaj kubokubo-okedroj
|
40{3}
30{4}
30{8}
|
240
|
120
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 5 grandaj kubokubo-okedroj
|
UC65
|

|
5
|
Grandaj kubokubo-okedroj
|
40{3}
30{4}
30{8/3}
|
240
|
120
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 5 grandaj rombo-sesedroj
|
UC66
|

|
5
|
Grandaj rombo-sesedroj
|
60{4}
30{8/3}
|
240
|
120
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 5 unuformaj grandaj rombokub-okedroj
|
UC67
|

|
5
|
Unuformaj grandaj rombokub-okedroj
|
40{3}
(30+60){4}
|
240
|
120
|
|
Dudekedra simetrio Ih
|
Kvaredra simetrio Th
|
| Kombinaĵo de 2 riproĉaj kuboj
|
UC68
|

|
2
|
Riproĉaj kuboj
|
(16+48){3}
12{4}
|
120
|
48
|
|
Okedra simetrio Oh
|
Okedra simetrio O
|
| Kombinaĵo de 2 riproĉaj dekduedroj
|
UC69
|

|
2
|
Riproĉaj dekduedroj
|
(40+120){3}
24{5}
|
300
|
120
|
|
Dudekedra simetrio Ih
|
Dudekedra simetrio I
|
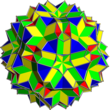
| Kombinaĵo de 2 grandaj riproĉaj dudek-dekduedroj
|
UC70
|
|
2
|
Grandaj riproĉaj dudek-dekduedroj
|
(40+120){3}
24{5/2}
|
300
|
120
|
|
Dudekedra simetrio Ih
|
Dudekedra simetrio I
|
| Kombinaĵo de 2 grandaj inversigitaj riproĉaj dudek-dekduedroj
|
UC71
|

|
2
|
Grandaj inversigitaj riproĉaj dudek-dekduedroj
|
(40+120){3}
24{5/2}
|
300
|
120
|
|
Dudekedra simetrio Ih
|
Dudekedra simetrio I
|
| Kombinaĵo de 2 grandaj malantaŭe riproĉaj dudek-dekduedroj
|
UC72
|

|
2
|
Grandaj malantaŭe riproĉaj dudek-dekduedroj
|
(40+120){3}
24{5/2}
|
300
|
120
|
|
Dudekedra simetrio Ih
|
Dudekedra simetrio I
|
| Kombinaĵo de 2 riproĉaj dekdu-dekduedroj
|
UC73
|

|
2
|
Riproĉaj dekdu-dekduedroj
|
120{3}
24{5}
24{5/2}
|
300
|
120
|
|
Dudekedra simetrio Ih
|
Dudekedra simetrio I
|
| Kombinaĵo de 2 inversigitaj riproĉaj dekdu-dekduedroj
|
UC74
|

|
2
|
Inversigitaj riproĉaj dekdu-dekduedroj
|
120{3}
24{5}
24{5/2}
|
300
|
120
|
|
Dudekedra simetrio Ih
|
Dudekedra simetrio I
|
| Kombinaĵo de 2 riproĉaj dudek-dekdu-dekduedroj
|
UC75
|

|
2
|
Riproĉaj dudek-dekdu-dekduedroj
|
(40+120){3}
24{5}
24{5/2}
|
360
|
120
|
|
Dudekedra simetrio Ih
|
Dudekedra simetrio I
|










































































