Anexo:Grupos de simetría esférica
 Simetría involutiva Cs, (*) [ ] = |
 Simetría cíclica Cnv, (*nn) [n] = |
 Simetría diédrica Dnh, (*n22) [n,2] = | |
| Grupo poliédrico, [n,3], (*n32) | |||
|---|---|---|---|
 Simetría tetraédrica Td, (*332) [3,3] = |
 Simetría octaédrica Oh, (*432) [4,3] = |
 Simetría icosaédrica Ih, (*532) [5,3] = | |
Los grupos de simetría esférica finita también se denominan grupos de puntos en tres dimensiones. Hay cinco clases de simetría que tienen dominios fundamentales triangulares: diédrico, cíclico, tetraédrico, octaédrico e icosaédrico.
Este artículo enumera los grupos utilizando la notación de Schoenflies, la notación de Coxeter,[1] y la notación orbifold,[2] y también figura su orden. John Conway utilizó una variación de la notación Schoenflies, basada en la estructura algebraica de los grupos de los cuaterniones, etiquetada con una o dos letras mayúsculas y subíndices de números enteros. El orden del grupo se define como el subíndice, a menos que el orden se duplique para los símbolos con un prefijo más o menos, "±", lo que implica una simetría central.[3]
También se proporciona la notación de Hermann-Mauguin (notación internacional). Los grupos cristalográficos, 32 en total, son un subconjunto con elementos de orden 2, 3, 4 y 6.[4]
Simetría involutiva
[editar]Hay cuatro grupos de simetría involutivas: sin simetría (C1), simetría especular (Cs), simetría rotacional doble (C2) y simetría central (Ci).
| Internac. | Geo |
Orbifold | Schöenflies | Conway | Coxeter | Orden | Abstracto | Dominio fundamental |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 11 | C1 | C1 | ][ [ ]+ |
1 | Z1 | 
|
| 2 | 2 | 22 | D1 = C2 |
D2 = C2 |
[2]+ | 2 | Z2 | 
|
| 1 | 22 | × | Ci = S2 |
CC2 | [2+,2+] | 2 | Z2 | 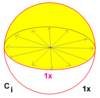
|
| 2 = m |
1 | * | Cs = C1v = C1h |
±C1 = CD2 |
[ ] | 2 | Z2 | 
|
Simetría cíclica
[editar]Hay cuatro familias de simetría cíclica infinitas, con n = 2 o superior. (n puede ser 1 como un caso especial, como sin simetría)
| Internac. | Geo |
Orbifold | Schöenflies | Conway | Coxeter | Orden | Abstracto | Dominio fundamental |
|---|---|---|---|---|---|---|---|---|
| 4 | 42 | 2× | S4 | CC4 | [2+,4+] | 4 | Z4 | 
|
| 2/m | 22 | 2* | C2h = D1d |
±C2 = ±D2 |
[2,2+] [2+,2] |
4 | Z4 | 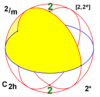
|
| Internac. | Geo |
Orbifold | Schöenflies | Conway | Coxeter | Orden | Abstracto | Dominio fundamental |
|---|---|---|---|---|---|---|---|---|
| 2 3 4 5 6 n |
2 3 4 5 6 n |
22 33 44 55 66 nn |
C2 C3 C4 C5 C6 Cn |
C2 C3 C4 C5 C6 Cn |
[2]+ [3]+ [4]+ [5]+ [6]+ [n]+ |
2 3 4 5 6 n |
Z2 Z3 Z4 Z5 Z6 Zn |

|
| 2mm 3m 4mm 5m 6mm nm (n es impar) nmm (n es par) |
2 3 4 5 6 n |
*22 *33 *44 *55 *66 *nn |
C2v C3v C4v C5v C6v Cnv |
CD4 CD6 CD8 CD10 CD12 CD2n |
[2] [3] [4] [5] [6] [n] |
4 6 8 10 12 2n |
D4 D6 D8 D10 D12 D2n |

|
| 3 8 5 12 - |
62 82 10.2 12.2 2n.2 |
3× 4× 5× 6× n× |
S6 S8 S10 S12 S2n |
±C3 CC8 ±C5 CC12 CC2n / ±Cn |
[2+,6+] [2+,8+] [2+,10+] [2+,12+] [2+,2n+] |
6 8 10 12 2n |
Z6 Z8 Z10 Z12 Z2n |

|
| 3/m=6 4/m 5/m=10 6/m n/m |
32 42 52 62 n2 |
3* 4* 5* 6* n* |
C3h C4h C5h C6h Cnh |
CC6 ±C4 CC10 ±C6 ±Cn / CC2n |
[2,3+] [2,4+] [2,5+] [2,6+] [2,n+] |
6 8 10 12 2n |
Z6 Z2×Z4 Z10 Z2×Z6 Z2×Zn ≅Z2n (n impar) |

|
Simetría diédrica
[editar]Hay tres familias de simetría diédrica infinitas, con n = 2 o superior (n puede ser 1 como caso especial).
| Internac. | Geo |
Orbifold | Schöenflies | Conway | Coxeter | Orden | Abstracto | Dominio fundamental |
|---|---|---|---|---|---|---|---|---|
| 222 | 2.2 | 222 | D2 | D4 | [2,2]+ | 4 | D4 | 
|
| 42m | 42 | 2*2 | D2d | DD8 | [2+,4] | 8 | D4 | 
|
| mmm | 22 | *222 | D2h | ±D4 | [2,2] | 8 | Z2×D4 | 
|
| Internac. | Geo |
Orbifold | Schöenflies | Conway | Coxeter | Orden | Abstracto | Dominio fundamental |
|---|---|---|---|---|---|---|---|---|
| 32 422 52 622 |
3.2 4.2 5.2 6.2 n.2 |
223 224 225 226 22n |
D3 D4 D5 D6 Dn |
D6 D8 D10 D12 D2n |
[2,3]+ [2,4]+ [2,5]+ [2,6]+ [2,n]+ |
6 8 10 12 2n |
D6 D8 D10 D12 D2n |
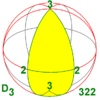
|
| 3m 82m 5m 12.2m |
62 82 10.2 12.2 n2 |
2*3 2*4 2*5 2*6 2*n |
D3d D4d D5d D6d Dnd |
±D6 DD16 ±D10 DD24 DD4n / ±D2n |
[2+,6] [2+,8] [2+,10] [2+,12] [2+,2n] |
12 16 20 24 4n |
D12 D16 D20 D24 D4n |

|
| 6m2 4/mmm 10m2 6/mmm |
32 42 52 62 n2 |
*223 *224 *225 *226 *22n |
D3h D4h D5h D6h Dnh |
DD12 ±D8 DD20 ±D12 ±D2n / DD4n |
[2,3] [2,4] [2,5] [2,6] [2,n] |
12 16 20 24 4n |
D12 Z2×D8 D20 Z2×D12 Z2×D2n ≅D4n (n impar) |

|
Simetría poliédrica
[editar]Hay tres tipos de simetría poliédrica: la simetría tetraédrica, la simetría octaédrica y la simetría icosaédrica, llamados así por los poliedros regulares de caras triangulares con estas simetrías.
| Internac. | Geo |
Orbifold | Schöenflies | Conway | Coxeter | Orden | Abstracto | Dominio fundamental |
|---|---|---|---|---|---|---|---|---|
| 23 | 3.3 | 332 | T | T | [3,3]+ = [4,3+]+ |
12 | A4 | 
|
| m3 | 43 | 3*2 | Th | ±T | [4,3+] | 24 | 2×A4 | 
|
| 43m | 33 | *332 | Td | TO | [3,3] = [1+,4,3] |
24 | S4 | 
|
| Internac. | Geo |
Orbifold | Schöenflies | Conway | Coxeter | Orden | Abstracto | Dominio fundamental |
|---|---|---|---|---|---|---|---|---|
| 432 | 4.3 | 432 | O | O | [4,3]+ = [[ 3,3]]+ |
24 | S4 | 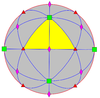
|
| m3m | 43 | *432 | Oh | ±O | [4,3] = [[ 3,3]] |
48 | 2×S4 | 
|
| Internac. | Geo |
Orbifold | Schöenflies | Conway | Coxeter | Orden | Abstracto | Dominio fundamental |
|---|---|---|---|---|---|---|---|---|
| 532 | 5.3 | 532 | I | I | [5,3]+ | 60 | A5 | 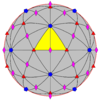
|
| 532/m | 53 | *532 | Ih | ±I | [5,3] | 120 | 2×A5 | 
|
Véase también
[editar]- Grupo de puntos cristalográficos
- Grupo triangular
- Anexo:Grupos de simetría plana
- Grupos de puntos en dos dimensiones
Referencias
[editar]- ↑ Johnson, 2015
- ↑ Conway, John H. (2008). The symmetries of things. Wellesley, Mass: A.K. Peters. ISBN 978-1-56881-220-5. OCLC 181862605.
- ↑ Conway, John; Smith, Derek A. (2003). On quaternions and octonions: their geometry, arithmetic, and symmetry. Natick, Mass: A.K. Peters. ISBN 978-1-56881-134-5. OCLC 560284450.
- ↑ Sands, 1993
Lecturas relacionadas
[editar]- Peter R. Cromwell, Polyhedra (1997), Appendix I
- Sands, Donald E. (1993). «Crystal Systems and Geometry». Introduction to Crystallography. Mineola, New York: Dover Publications, Inc. p. 165. ISBN 0-486-67839-3.
- On Quaternions and Octonions, 2003, John Horton Conway and Derek A. Smith ISBN 978-1-56881-134-5
- The Symmetries of Things 2008, John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ISBN 978-1-56881-220-5
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
- N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite symmetry groups, Table 11.4 Finite Groups of Isometries in 3-space
Enlaces externos
[editar]- Grupos de simetría esférica finita
- Weisstein, Eric W. «Schoenflies symbol». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Weisstein, Eric W. «Crystallographic point groups». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Poliedros canónicos más simples de cada tipo de simetría, por David I. McCooey