Brotes (juego)
Brotes (en inglés sprouts) o juego del drago es un juego de lápiz y papel con interesantes propiedades matemáticas. Los primeros que lo jugaron fueron los matemáticos John Horton Conway y Michael S. Paterson en la Universidad de Cambridge en 1967.
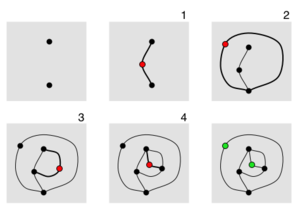
Se trata de un juego para dos o más jugadores, que comienza con unos pocos puntos (llamados brotes) en una hoja de papel. Por turnos, los jugadores van uniendo un brote con otro (o consigo mismo) mediante una línea (llamada rama) y añadiendo un nuevo brote sobre la línea recién dibujada. El dibujo de las nuevas ramas tiene ciertas restricciones:
- Puede tener cualquier trazado, siempre que no se corte a sí misma o a otra línea ya dibujada.
- Una rama no puede pasar por otros brotes distintos del inicial y el final de la misma.
- De ningún brote pueden salir más de tres ramas, quedando un brote anulado (o muerto) cuando cumple esta condición.
Pierde el juego el jugador que no es capaz de trazar una nueva rama cumpliendo las condiciones anteriores.
El diagrama de la derecha muestra una partida que se inicia con dos puntos. Después del cuarto movimiento, la mayoría de los brotes están muertos pues de ellos salen tres líneas. Comoquiera que es imposible realizar un nuevo movimiento, el primer jugador pierde la partida.
Análisis del juego
[editar]Se puede demostrar que todas las partidas de drago terminan, en particular si se comienza el juego con n brotes cada partida tendrá entre 2n y 3n - 1 movimientos.[1]
Al no ser posibles los empates y tener las partidas un número finito de movimientos se sabe que ganará siempre uno de los dos jugadores. Así, se ha demostrado que si hay dos brotes iniciales puede ganar siempre el segundo jugador, si hay 3, 4 o 5 brotes el primer jugador tiene estrategia ganadora, si son 6, 7 o 8 brotes el segundo jugador tiene asegurada una estrategia ganadora y si son 9, 10 o 11 la tiene el primero.[1]
En general se ha conjeturado que el primer jugador tiene asegurada la victoria si al dividir el número inicial de brotes entre 6 deja resto 3, 4 o 5 y en caso contrario ganará siempre, si sabe jugar, el segundo jugador.[1] La conjetura solo se ha demostrado para cuando los números iniciales de brotes son hasta 44, y también para 46, 47 o 53.[1]
Referencias
[editar]Enlaces externos
[editar]- Madras College Mathematics Department, "Mathematical Games: Sprouts."
- Ivars Peterson, "Sprouts for Spring," Science News Online.
- Danny Purvis, World Game of Sprouts Association.
- The Game of Sprouts en la Universidad de Utah (con un applet interactivo para una partida entre humanos).