Catenoide

Película de jabón entre dos aros.

Una catenoide es un tipo de superficie que se obtiene por rotación de una catenaria alrededor de un eje coplanario, perpendicular al eje de simetría y que no la corte.^[1]​ Se trata de una superficie mínima o minimal, lo que significa que ocupa el área mínima cuando está delimitada por un espacio cerrado.^[2]​ Fue descrita formalmente en 1744 por el matemático Leonhard Euler.

Una película de jabón unida a anillos circulares gemelos, a causa de la tensión superficial, tomará la forma de una catenoide.^[2]​ Debido a que son miembros de la misma familia asociada de superficies, una catenoide se puede doblar en una porción de un helicoide y viceversa.

Geometría

Una catenoide

Obtención de una catenoide a partir de la rotación de una catenaria

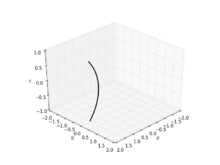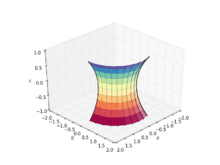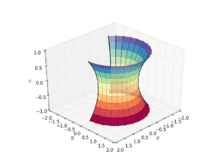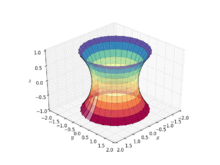
La catenoide fue la primera superficie mínima no trivial en el espacio euclidiano tridimensional que se descubrió aparte del plano. La catenoide se obtiene al rotar una catenaria sobre su directriz.^[3]​ Fue encontrada y probado que era un mínimo por Leonhard Euler en 1744.^[4]​^[5]​ El primer trabajo sobre el tema fue publicado también por Jean Baptiste Meusnier.^[6]​^[5]​^: 11106 Solo hay dos superficies mínimas de revolución (superficies de revolución que también son superficies mínimas): el plano y la catenoide.^[7]​

La catenoide se puede definir mediante las siguientes ecuaciones paramétricas:

${\displaystyle x=c\cosh {\frac {v}{c}}\cos u}$

${\displaystyle y=c\cosh {\frac {v}{c}}\operatorname {sen} u}$

${\displaystyle z=v}$

donde:${\displaystyle u\in [-\pi ,\pi )}$ y ${\displaystyle v\in \mathbb {R} }$ y ${\displaystyle c}$ una constante real distinta de cero.

En coordenadas cilíndricas:

${\displaystyle \rho =c\cosh {\frac {z}{c}}}$

donde ${\displaystyle c}$ es una constante real.

Se puede formar un modelo físico de una catenoide sumergiendo dos anillos circulares en una solución jabonosa y separando lentamente los círculos.

La catenoide también se puede definir aproximadamente mediante el método de cuadrícula estirada como un modelo 3D facetado.

Transformación helicoide

Animación que muestra un helicoide deformándose en un catenoide y vuelta a un helicoide

Como son miembros de la misma familia asociada de superficies, se puede doblar una catenoide en una porción de un helicoide sin estirarse. En otras palabras, se puede hacer (en su mayoría) una deformación continua e isométrica de una catenoide hasta una porción del helicoide de tal manera que cada miembro de la familia de deformación sea mínimal (teniendo una curvatura media de cero). Una parametrización de tal deformación es dada por el sistema:

${\displaystyle x(u,v)=\cos \theta \,\sinh v\,\operatorname {sen} u+\operatorname {sen} \theta \,\cosh v\,\cos u}$

${\displaystyle y(u,v)=-\cos \theta \,\sinh v\,\cos u+\operatorname {sen} \theta \,\cosh v\,\operatorname {sen} u}$

${\displaystyle z(u,v)=u\cos \theta +v\operatorname {sen} \theta }$

para ${\displaystyle (u,v)\in (-\pi ,\pi ]\times (-\infty ,\infty )}$, con parámetros de deformación ${\displaystyle -\pi <\theta \leq \pi }$, donde:

${\displaystyle \theta =\pi }$ corresponde a un helicoide diestro,

${\displaystyle \theta =\pm \pi /2}$ corresponde a una catenoide, y

${\displaystyle \theta =0}$ corresponde a un helicoide zurdo.

Véase también

• Hiperboloide

Notas

1. Dierkes, Ulrich; Hildebrandt, Stefan; Sauvigny, Friedrich (2010). Minimal Surfaces (en inglés). Springer Science & Business Media. p. 141. ISBN 9783642116988. 
2. «zona catenoide». Real Academia de Ingeniería. 
3. Gullberg, Jan (1997). Mathematics: From the Birth of Numbers (en inglés). W. W. Norton & Company. p. 538. ISBN 9780393040029. 
4. Helveticae, Euler, Leonhard (1952). Carathëodory Constantin, ed. Methodus inveniendi lineas curvas: maximi minimive proprietate gaudentes sive solutio problematis isoperimetrici latissimo sensu accepti (en latin). Springer Science & Business Media. ISBN 3-76431-424-9. 
5. Colding, T. H.; Minicozzi, W. P. (17 de julio de 2006). «Shapes of embedded minimal surfaces». Proceedings of the National Academy of Sciences 103 (30): 11106-11111. PMC 1544050. doi:10.1073/pnas.0510379103. 
6. Meusnier, J. B (1881). Mémoire sur la courbure des surfaces [Memory on the curvature of surfaces.] (PDF) (en francés). Bruxelles: F. Hayez, Imprimeur De L'Acdemie Royale De Belgique. pp. 477-510. ISBN 9781147341744. 
7. «Catenoid». Wolfram MathWorld (en inglés). Archivado desde el original el 28 de diciembre de 2013. Consultado el 15 de enero de 2017. 

Referencias

• Esta obra contiene una traducción derivada de «Catenoid» de Wikipedia en inglés, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 4.0 Internacional.

Bibliografía

• Krivoshapko, Sergey; Ivanov, V. N. (2015). «Minimal Surfaces». Encyclopedia of Analytical Surfaces (en inglés). Springer. ISBN 9783319117737. 

Enlaces externos

• Hazewinkel, Michiel, ed. (2001), «Catenoide», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104 .
• Catenoid - WebGL model
• Euler's text describing the catenoid at Carnegie Mellon University
• mathcurve.com
• upc.es
• serge.mehl.free.fr