Construcción de Wythoff

En geometría, una construcción de Wythoff, que lleva el nombre del matemático Willem Abraham Wythoff, es un método para construir un poliedro uniforme o teselado.[1] A menudo también se la conoce como construcción caleidoscópica de Wythoff.[2]
Proceso de construcción
[editar]El método se basa en la idea de teselar una esfera, usando triángulos esféricos (véase triángulo de Schwarz). Esta construcción dispone tres espejos a los lados de un triángulo, como en un caleidoscopio. Sin embargo, a diferencia de un caleidoscopio, los espejos no son paralelos, sino que se cruzan en un solo punto. Por tanto, encierran un triángulo esférico en la superficie de cualquier esfera centrada en ese punto y las reflexiones repetidas producen una multitud de copias del triángulo. Si los ángulos del triángulo esférico se eligen apropiadamente, los triángulos formarán teselados en la esfera, una o más veces.
Si se coloca un vértice en un punto adecuado dentro del triángulo esférico encerrado por los espejos, es posible asegurar que los reflejos de ese punto produzcan un poliedro uniforme. Para un triángulo esférico ABC se tienen cuatro posibilidades que producirán un poliedro uniforme:
- Se coloca un vértice en el punto A. Esto produce un poliedro con el símbolo de Wythoff a|b c, donde a es igual a π dividido por el ángulo del triángulo en A, y de manera similar para b y c.
- Se coloca un vértice en un punto de la línea AB, de modo que biseca el ángulo de C. Esto produce un poliedro con el símbolo de Wythoff a b|c.
- Se coloca un vértice de manera que esté en el incentro de ABC. Esto produce un poliedro con el símbolo de Wythoff a b c|.
- El vértice está en un punto tal que, cuando se gira alrededor de cualquiera de las esquinas del triángulo el doble del ángulo en ese punto, se desplaza la misma distancia para cada ángulo. Solo se utilizan reflexiones pares del vértice original. El poliedro tiene el símbolo de Wythoff |a b c.
El proceso en general también se aplica a politopos regulares de dimensiones superiores, incluidos los 4-politopos uniformes (de 4 dimensiones).
  El prisma hexagonal se construye a partir de cualquiera de las dos familias (6 2 2) y (3 2 2) |
  El teselado cuadrado truncado es construido por dos diferentes posiciones de simetría en la familia (4 4 2) |
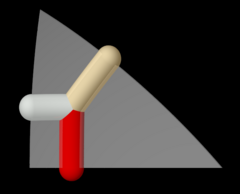 Patrón de Wythoff pq2|= 432|. 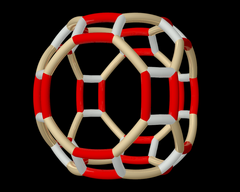 Órbita del patrón de Wythoff de arriba, bajo la acción de la simetría octaédrica completa |
Construcciones no wythoffianas
[editar]Los politopos uniformes que no se pueden crear mediante una construcción de espejo Wythoff se denominan no Wythoffianos. Generalmente pueden derivarse de formas wythoffianas mediante alternación (eliminación de vértices alternativos) o mediante la inserción de capas alternas de figuras parciales. Ambos tipos de figuras poseerán simetría rotacional. A veces las formas romas se consideran wythoffianas, aunque solo pueden construirse mediante la alternancia de formas omnitruncadas.
 The antiprisma hexagonal is constructed by an alternation of a dodecagonal prism. |
 The elongated triangular tiling is constructed by a layering of teselado cuadrado and teselado triangular rows. |
 The great dirhombicosidodecahedron is the only non-Wythoffian uniform polyhedron. |
Véase también
[editar]- Símbolo de Wythoff: simbología correspondiente a la construcción de Wythoff de poliedros uniformes y teselados uniformes.
- Diagrama de Coxeter-Dynkin: simbología generalizada para la construcción Wythoff de politopos uniformes y panales.
Referencias
[editar]- ↑ H. S. M. Coxeter (2012). Regular Polytopes. Courier Corporation. p. 368. ISBN 9780486141589. Consultado el 22 de agosto de 2023.
- ↑ Joseph Needham (1962). Science and Civilisation in China. Cambridge University Press. pp. 93 de 434. ISBN 9780521058025. Consultado el 22 de agosto de 2023.
Bibliografía
[editar]- Coxeter Regular Polytopes, Tercera edición, (1973), edición de Dover, ISBN 0-486-61480-8 (Capítulo V: El caleidoscopio, Sección: 5.7 La construcción de Wythoff)
- Coxeter La belleza de la geometría: doce ensayos, Publicaciones de Dover, 1999, ISBN 0-486-40919-8 (Capítulo 3: Construcción de Wythoff para politopos uniformes)
- Har'El, Z. Solución uniforme para poliedros uniformes, Geometriae Dedicata 47, 57-110, 1993. pdf (Sección 4: El Caleidoscopio)
- W.A. Wythoff, Una relación entre los politopos de la familia C600, Koninklijke Akademie van Wetenschappen te Amsterdam, Actas de la Sección de Ciencias, 20 (1918) 966–970.
Enlaces externos
[editar]- El subprograma de Greg Egan para mostrar poliedros uniformes utilizando el método de construcción de Wythoff
- Una representación de Shadertoy del método de construcción de Wythoff
- Jenn, software que genera vistas de poliedros y policoras (esféricos) a partir de grupos de simetría