Dodecaedro truncado

Dodecaedro truncado
Grupo	Sólidos de Arquímedes
Número de caras	32
Polígonos que forman las caras	20 triángulos equiláteros 12 decágonos equiláteros
Número de aristas	90
Número de vértices	60
Tipo de Vértice	Uniforme de orden 3
Caras relacionadas en los vértices	2 decágonos 1 triángulo
Simetría	Icosaédrica (Ih)
Poliedro dual	Triaquisicosaedro
Propiedades	Poliedro convexo, de vértices uniformes
Desarrollo del dodecaedro truncado

El dodecaedro truncado es un sólido de Arquímedes que se obtiene truncando cada vértice de un dodecaedro. Posee 12 caras regulares decagonales, 20 caras regulares triangulares, 60 vértices y 90 aristas.

Relaciones geométricas

Este poliedro se puede formar a partir de un dodecaedro regular mediante truncado (cortando sus esquinas), de modo que las caras pentagonales se conviertan en decágonos y las esquinas se conviertan en triángulos equiláteros.

Se utiliza en el teselado celdas-transitivo que llena el espacio hiperbólico, el panal icosaédrico bitruncado.

Área y volumen

El área A y el volumen V de un dodecaedro truncado de longitud de arista a son:

${\displaystyle {\begin{aligned}A&=5\left({\sqrt {3}}+6{\sqrt {5+2{\sqrt {5}}}}\right)a^{2}&&\approx 100.990\,76a^{2}\\V&={\tfrac {5}{12}}\left(99+47{\sqrt {5}}\right)a^{3}&&\approx 85.039\,6646a^{3}\end{aligned}}}$

Coordenadas cartesianas

Las coordenadas cartesianas para los vértices de un dodecaedro truncado con longitud de arista 2φ − 2, centrado en el origen,^[1]​ son todas las permutaciones pares de:

(0, ±1/φ, ±(2 + φ))

(±1/φ, ±φ, ±2φ)

(±φ, ±2, ±(φ + 1))

donde φ = 1 + √5/2 es el número áureo.

Proyecciones ortogonales

El dodecaedro truncado tiene cinco proyecciones ortogonales especiales, centradas en: un vértice, en dos tipos de aristas y dos tipos de caras. Los dos últimos corresponden a los planos de Coxeter A₂ y H₂.

Proyecciones ortogonales

Centradas en	Vértices	Arista 3-3	Arista 10-10	Cara triangular	Cara Decagonal
Sólido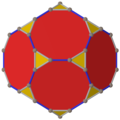
Alámbrico
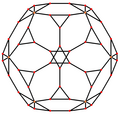
Simetría proyectiva	[2]	[2]	[2]	[6]	[10]
Dual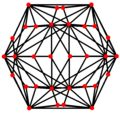

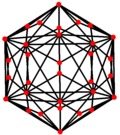
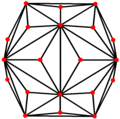
Teselaciones esféricas y diagramas de Schlegel

El dodecaedro truncado también se puede representar como un poliedro esférico y proyectarse sobre el plano a través de una proyección estereográfica. Esta proyección es conforme, preservando los ángulos pero no las áreas ni las longitudes. Las líneas rectas sobre la esfera se proyectan como arcos circulares sobre el plano.

Los diagramas de Schlegel son similares, con una proyección perspectiva y aristas rectas.

Proyección ortogonal	Proyecciones estereográficas
	Centrada en decágono	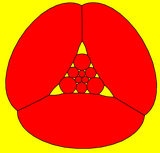Centrada en triángulo

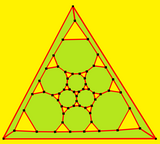
Disposición de vértices

Comparte su disposición de vértices con tres poliedros uniformes estrellados:

Dodecaedro truncado

Gran icosicosidodecaedro

Gran dodecicosidodecaedro ditrigonal

Gran dodecicosaedro

Poliedros y teselados relacionados

Es parte de un proceso de truncamiento entre un dodecaedro y un icosaedro:

Familia de poliedros icosaédricos uniformes
Simetría: [5,3], (*532)							[5,3]^+, (532)
{5,3}	t{5,3}	r{5,3}	t{3,5}	{3,5}	rr{5,3}	tr{5,3}	sr{5,3}
Duales de los poliedros uniformes
V5.5.5	V3.10.10	V3.5.3.5	V5.6.6	V3.3.3.3.3	V3.4.5.4	V4.6.10	V3.3.3.3.5

Este poliedro está topológicamente relacionado como parte de la secuencia de poliedros uniformes truncados con configuración de vértices (3.2n.2n) y simetría [n,3] del grupo de Coxeter.

*Mutación de simetría n32 de teselados esféricos truncados: t{n,3}
Simetría *n32 [n,3]	Esférica				Euclídea	Hiperbólica compacta		Paracompacta
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]...	*∞32 [∞,3]
Formas truncadas
Símbolo	t{2,3}	t{3,3}	t{4,3}	t{5,3}	t{6,3}	t{7,3}	t{8,3}	t{∞,3}
Triaquis figuras
Config.	V3.4.4	V3.6.6	V3.8.8	V3.10.10	V3.12.12	V3.14.14	V3.16.16	V3.∞.∞

Grafo del dodecaedro truncado

Grafo del dodecaedro truncado
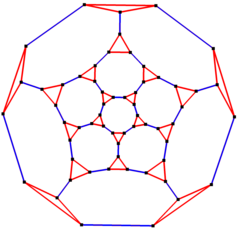Diagrama de Schlegel, con simetría de 5 lóbulos
Vértices	60
Aristas	90
Automorfismos	120
Número cromático	2
Propiedades	Cúbico, hamiltoniano, regular, cero-simétrico
[editar datos en Wikidata]

En el campo de la teoría de grafos, el grafo del dodecaedro truncado es el esquema de vértices y aristas del dodecaedro truncado, uno de los sólidos arquimedianos. Tiene 60 vértices y 90 líneas, y es un grafo arquimediano cúbico.^[2]​

Circular

Véase también

• Sólidos platónicos
• Sólidos de Johnson
• Sólidos de Catalan
• Poliedro dual
• Poliedros

Referencias

1. Weisstein, Eric W. «Icosahedral group». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
2. Read, R. C.; Wilson, R. J. (1998), An Atlas of Graphs, Oxford University Press, p. 269 .

Bibliografía

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X.  (Sección 3-9)
• Cromwell, P. (1997). Polyhedra. United Kingdom: Cambridge. pp. 79–86 Archimedean solids. ISBN 0-521-55432-2. 

Enlaces externos

• Weisstein, Eric W. «Truncated dodecahedron». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
  • Weisstein, Eric W. «Truncated dodecahedral graph». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Klitzing, Richard. «3D convex uniform polyhedra o3x5x - tid». 

• JrpIJTarRzJGitPNEnHrk3rNm5pr6Gzui1P5MD7RwSrFu6TKzjy5qQl5PYokM9mcFWcoPivzjQxlRGa1eVpVmZl5Uv2nXTaX5RSgc2N5B3daPbsAUEsCGxrnbgMLCKvMvztIjl44GGTstwl3pC589 OwhVUTHvkTzg6b4dpshGHQn4ajtxQA8ch==W1wKBsKuMpbqE4oCXbIi2sfEgppN1tcDBWVOJUXQfPiEglU1jtQi7fUj5xDW2PpZtdwQDmwpC3Lk&name=Truncado+Dodecaedro#applet Red imprimible editable de un dodecaedro truncado con vista 3D interactiva
• Los poliedros uniformes
• Poliedros de realidad virtual La enciclopedia de poliedros