Leyes de Cassini

Las leyes de Cassini son una descripción compacta del movimiento de la Luna. Las mismas fueron formuladas en 1693 por Giovanni Domenico Cassini, un destacado científico de su época.[1]​

Se han realizado ciertos refinamientos de las leyes para incluir libraciones físicas,[1]​ y han sido generalizadas para aplicarlas a otros satélites y planetas.[2]​[3]​

Leyes de Cassini

[editar]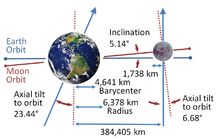
Inclinación de la órbita y rotación.
  1. La Luna posee una resonancia órbita-spin 1:1. Esto significa que la relación entre la rotación / órbita de la Luna es tal que es siempre la misma cara de la Luna la que enfrenta la Tierra.
  2. El eje rotacional de la Luna mantiene el mismo ángulo de inclinación respecto del plano eclíptico. El eje rotacional de la Luna forma un cono cuya intersección con el plano eclíptico forma un círculo.
  3. Un plano formado por una superficie normal al plano de la eclíptica y una normal al plano orbital de la Luna contiene el eje rotacional de la Luna.

En el caso de la Luna, su eje rotacional siempre apunta unos 1,5 grados desviado respecto al polo Norte de la eclíptica. Las normales al plano orbital y el eje rotacional se encuentran siempre en lados opuestos de la normal a la eclíptica.

Por lo tanto, la normal al plano orbital y el eje rotacional de la Luna poseen una preseción alrededor del polo eclíptico con el mismo período. El período es de unos 18 años y el movimiento es retrógrado.

Estado de Cassini

[editar]

Un sistema que obedece a estas leyes se dice que se encuentra en un estado de Cassini, es decir: un estado rotacional en el cual el eje de spin, la normal a la órbita, y la normal al plano de Laplace con coplanares mientras que la oblicuidad permanece constante.[2]​[4]​ El plano Laplace se define como el plano con respecto al cual la órbita del planeta precede con una inclinación constante con respecto a los planos ecuatorial y eclíptico[4]​

Referencias

[editar]
  1. ↑ a b For the original statement of the laws, see V V Belet︠s︡kiĭ (2001). Essays on the Motion of Celestial Bodies. Birkhäuser. p. 181. ISBN 3-7643-5866-1. 
  2. ↑ a b Marie Yseboodt & Jean-Luc Margot Evolution of Mercury’s obliquity
  3. ↑ V V Belet︠s︡kiĭ (2001). Essays on the Motion of Celestial Bodies. Birkhäuser. p. 179. ISBN 3-7643-5866-1. 
  4. ↑ a b Y. Calisesi (2007). Solar Variability and Planetary Climates. Springer. p. 34. ISBN 0-387-48339-X. 

Bibliografía

[editar]