Método neusis

Construcción neusis

Neusis es un método de construcción geométrica,^[1]​ en el que se emplea una regla en la que se marca una distancia que debe encajarse entre dos curvas, y que además debe pasar por un punto dado. Fue utilizado en la antigüedad por matemáticos griegos, aunque estaba considerado un recurso atípico que solo se debía emplear para abordar determinados problemas cuya resolución no parecía posible usando exclusivamente regla y compás (en los que no se admite valerse de una regla con una marca de distancia).

Construcción geométrica

La construcción neusis (del griego νεῦσις de νεύειν neuein "dirección de inclinación"; plural: νεύσεις neuseis) consiste en ajustar la posición de un segmento rectilíneo de longitud prefijada (denominada diastema, de la palabra griega "διάστημα", que significa "distancia") entre dos curvas dadas (denominadas curva directriz y curva de ajuste), de manera que el segmento o su extensión, pasa a través de un punto dado denominado polo. Dicho de otra forma, la posición buscada debe cumplir tres condiciones: uno de los extremos del segmento tiene que situarse sobre la curva directriz; el otro extremo tiene que situarse sobre la curva de ajuste; y el segmento o su prolongación debe pasar por el polo.

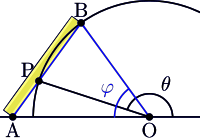
Una construcción neusis se debe realizar mediante el uso de la 'regla neusis': una regla que puede hacer rotaciones alrededor del polo (lo que se puede realizar poniendo una chincheta en el polo y después presionando la regla contra la chincheta). En la figura, una de las terminaciones de la regla está marcada con un círculo amarillo, cuyo centro coincide con el origen de la división de la escala de la regla. Una segunda marca en la regla (el círculo azul) indica la distancia dada, denominada diastema. La marca amarilla se mueve a lo largo de la curva directriz, hasta que la marca azul coincide con la curva de ajuste. La posición del segmento encontrado de esta forma se muestra en la figura con el punto remarcado en azul y el punto remarcado en rojo.

Trisección neusis de un ángulo >135° para encontrar φ=θ/3, utilizando solo la longitud de la regla. El radio del arco es igual a la longitud de la regla. Para ángulos θ<135° se aplica la misma construcción, pero con P extendido más allá de AB

Usos de la neusis

La neusis ha sido importante porque a veces provee una forma de resolver problemas geométricos que no se pueden solucionar a través de construcciones con regla y compás únicamente. Ejemplos son la trisección de cualquier ángulo en tres partes iguales, o la construcción de un heptágono regular.^[2]​ Matemáticos tales como Arquímedes de Siracusa (287–212 a. C.) utilizaban neuseis libremente, y siglos después Isaac Newton continuaba empleando este procedimiento.^[3]​ Sin embargo, la técnica cayó en desuso gradualmente.

Se sabe que un n-ágono regular es construible mediante neusis para n=

3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 24, 26, 27, 28, 30 , 32, 33, 34, 35, 36, 37, 38, 39, 40, 42, 44, 45, 48, 51, 52, 54, 55, 56, 57, 60, 63, 64, 65, 66, 68 , 70, 72, 73, 74, 76, 77, 78, 80, 81, 84, 85, 88, 90, 91, 95, 96, 97, 99, 102, 104, 105, 108, 109, 110, 111 , 112, 114, 117, 119, 120, 126, 128, ... (sucesión A122254 en OEIS).

Benjamin y Snyder descubrieron en 2014 que el endecágono regular es neusis-construible.^[4]​

Desuso

El historiador de las matemáticas Thomas Little Heath, sugirió que Enópides (440 a. C.) fue el primero de los matemáticos griegos en poner las construcciones con regla y compás por encima de las neuseis. El principio de evitar neuseis siempre que fuera posible, pudo ser difundido por Hipócrates de Quíos (430 a. C.), originario de la misma isla que Oenopides, y quien fue —por lo que se sabe— el primero en escribir libros sobre geometría sistemática y ordenada. Cien años después de él Euclides también evitó neuseis en su muy influyente libro, Los Elementos.

El siguiente ataque a la neusis vino cuando, desde el siglo IV a. C., el idealismo de Platón ganó terreno. Bajo su influencia se desarrolló una jerarquía de tres tipos de construcciones geométricas. Descendiendo desde lo "abstracto y noble" hasta lo "mecánico y terrenal", las tres clases eran:

1. Construcciones solo con líneas rectas y circunferencias (regla y compás);
2. Construcciones que además utilizaban las secciones cónicas (elipses, parábolas, hipérbolas);
3. Construcciones que necesitan otras técnicas, como por ejemplo neuseis.

Al final el uso de neusis fue tomado como aceptable solamente cuando las otras dos categorías de construcción más elevadas no ofrecían una solución. Neusis se convirtió en un tipo de recurso de última necesidad que se utilizaba cuando todos los demás métodos, más respetables, habían fallado. Utilizar neusis cuando los otros métodos podían haber sido utilizados fue marcado por el matemático griego Pappus de Alejandría (325 d. C.) como un "error a considerar".

Véase también

• Trisección del ángulo
• Duplicación del cubo
• Cuadratura del círculo

Referencias

1. Euclides (2016). Elementos. Libros I-IV. RBA Libros. p. 368. ISBN 9788424931926. Consultado el 24 de marzo de 2021. 
2. Weisstein, Eric W. "Neusis Construction." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/NeusisConstruction.html
3. Guicciardini, Niccolò (2009). Isaac Newton on Mathematical Certainty and Method, Issue 4. M.I.T Press. p. 68. ISBN 9780262013178. 
4. Benjamin, Elliot; Snyder, C (May 2014). «On the construction of the regular hendecagon by marked ruler and compass». Mathematical Proceedings of the Cambridge Philosophical Society 156 (3): 409-424. doi:10.1017/S0305004113000753. Archivado desde el original el 26 de septiembre de 2020. Consultado el 26 de septiembre de 2020. 

Bibliografía

• R. Boeker, 'Neusis', in: Paulys Realencyclopädie der Classischen Altertumswissenschaft, G. Wissowa red. (1894–), Supplement 9 (1962) 415–461.–In German. La revisión más comprensiva; sin embargo, el autor tiene opiniones curiosas a veces.
• T. L. Heath, A history of Greek Mathematics (2 volumes; Oxford 1921).
• H. G. Zeuthen, Die Lehre von den Kegelschnitten im Altertum [= The Theory of Conic Sections in Antiquity] (Copenhagen 1886; reprinted Hildesheim 1966).

Enlaces externos

• Weisstein, Eric W. «NeusisConstruction». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research. 
• Trisección del ángulo por Paper Folding, inglés