Procesamiento digital de imágenes

El procesamiento de imágenes digitales o filtro de imagen es el conjunto de técnicas que se aplican a las imágenes digitales con el objetivo de mejorar la calidad o facilitar la búsqueda de información.

Proceso de filtrado

Es el conjunto de técnicas englobadas dentro del preprocesamiento de imágenes cuyo objetivo fundamental es obtener, a partir de una imagen origen, otra final cuyo resultado sea más adecuado para una aplicación específica mejorando ciertas características de la misma que posibilite efectuar operaciones del procesado sobre ella.

Los principales objetivos que se persiguen con la aplicación de filtros son:

Suavizar la imagen: reducir la cantidad de variaciones de intensidad entre píxeles vecinos.
Eliminar ruido: eliminar aquellos píxeles cuyo nivel de intensidad es muy diferente al de sus vecinos y cuyo origen puede estar tanto en el proceso de adquisición de la imagen como en el de transmisión.
Realzar bordes: destacar los bordes que se localizan en una imagen.
Detectar bordes: detectar los píxeles donde se produce un cambio brusco en la función intensidad.

Por tanto, se consideran los filtros como operaciones que se aplican a los píxeles de una imagen digital para optimizarla, enfatizar cierta información o conseguir un efecto especial en ella.

El proceso de filtrado puede llevarse a cabo sobre los dominios de frecuencia y/o espacio.

Filtrado en el dominio de la frecuencia

Los filtros de frecuencia procesan una imagen trabajando sobre el dominio de la frecuencia en la Transformada de Fourier de la imagen. Para ello, esta se modifica siguiendo el Teorema de la Convolución correspondiente:

se aplica la Transformada de Fourier,
se multiplica posteriormente por la función del filtro que ha sido escogido,
para concluir re-transformándola al dominio espacial empleando la Transformada Inversa de Fourier.

Teorema de la Convolución (frecuencia): $G(u,v)=F(u,v)*H(u,v)$

F(u,v): transformada de Fourier de la imagen original.

H(u,v): filtro atenuador de frecuencias.

Como la multiplicación en el espacio de Fourier es idéntica a la convolución en el dominio espacial, todos los filtros podrían, en teoría, ser implementados como un filtro espacial. Etapas del procesamiento de imágenes en el dominio de la frecuencia.

Tipos

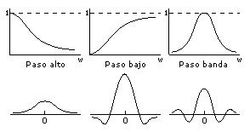
Existen básicamente tres tipos distintos de filtros que pueden aplicarse:

Filtro paso bajo: atenúa las frecuencias altas y mantiene sin variaciones las bajas. El resultado en el dominio espacial es equivalente al de un filtro de suavizado, donde las altas frecuencias que son filtradas se corresponden con los cambios fuertes de intensidad. Consigue reducir el ruido suavizando las transiciones existentes.
Filtro paso alto: atenúa las frecuencias bajas manteniendo invariables las frecuencias altas. Puesto que las altas frecuencias corresponden en las imágenes a cambios bruscos de densidad, este tipo de filtros es usado, porque entre otras ventajas, ofrece mejoras en la detección de bordes en el dominio espacial, ya que estos contienen gran cantidad de dichas frecuencias. Refuerza los contrastes que se encuentran en la imagen.
Filtro paso banda: atenúa frecuencias muy altas o muy bajas manteniendo una banda de rango medio.

Ventajas

Método simple y sencillo de implementar.
Fácil asociación del concepto de frecuencia con ciertas características de la imagen; cambios de tonalidad suaves implican frecuencias bajas y cambios bruscos frecuencias altas.
Proporciona flexibilidad en el diseño de soluciones de filtrado.
Rapidez en el filtrado al utilizar el Teorema de la Convolución.

Desventajas

Se necesitan conocimientos en varios campos para desarrollar una aplicación para el procesamiento de imágenes.
El ruido no puede ser eliminado completamente.

Filtrado en el dominio del espacio

Las operaciones de filtrado se llevan a cabo directamente sobre los píxeles de la imagen. En este proceso se relaciona, para todos y cada uno de los puntos de la imagen, un conjunto de píxeles próximos al píxel objetivo con la finalidad de obtener una información útil, dependiente del tipo de filtro aplicado, que permita actuar sobre el píxel concreto en que se está llevando a cabo el proceso de filtrado para, de este modo, obtener mejoras sobre la imagen y/o datos que podrían ser utilizados en futuras acciones o procesos de trabajo sobre ella.

Los filtros en el dominio del espacio pueden clasificarse en:

Filtros lineales (filtros basados en núcleos o máscaras de convolución).
Filtros no lineales.

El concepto de núcleo se entiende como una matriz de coeficientes donde el entorno del punto (x,y) que se considera en la imagen para obtener g(x,y) está determinado por el tamaño y forma del núcleo seleccionado. Aunque la forma y tamaño de esta matriz es variable y queda a elección de cada usuario, es común el uso de núcleos cuadrados nxn. Dependiendo de la implementación, en los límites de la imagen se aplica un tratamiento especial (se asume un marco exterior de ceros o se repiten los valores del borde) o no se aplica ninguno. Es por ello, que el tipo de filtrado queda establecido por el contenido de dicho núcleo utilizado.

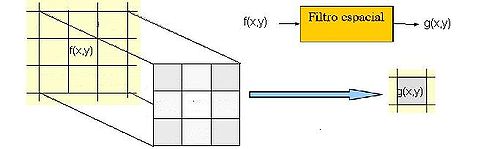
Para realizar un filtrado en el dominio del espacio se realiza una convolución (barrido) del núcleo sobre la imagen. Para ello se sigue el Teorema de Convolución en el espacio: g(x,y) = h(x,y) * f(x,y)

Cada píxel de la nueva imagen se obtiene mediante el sumatorio de la multiplicación del núcleo por los píxeles contiguos:
g(x,y) = ∑∑ f(i,j) w(i,j)
Generalmente se divide sobre cierto valor constante para normalizar que suele obtenerse de la suma de los valores del núcleo empleado.

Tipos

Filtro paso bajo (suavizamiento): utilizados para eliminar ruido o detalles pequeños de poco interés puesto que solo afecta a zonas con muchos cambios. La frecuencia de corte se determina por el tamaño del núcleo y sus coeficientes. Se emplean diversos núcleos:
- Promedio: promedio de píxeles vecinos (núcleos de unos).
- Paso bajo en frecuencia.
- Media: reemplaza cada píxel por el valor medio de sus contiguos.
- Mediana: sustituye por el valor de la mediana de los píxeles vecinos (normalmente se comporta mejor que el de promedio).
- Gaussiano: aproximación a la distribución gaussiana.
Filtro paso alto (atenuamiento): intensifica los detalles, bordes y cambios de alta frecuencia, mientras que atenúa las zonas de tonalidad uniforme. Esto permite una mejor identificación posterior de los objetos que se encuentren en la imagen, puesto que el brillo se hace mayor en las zonas con frecuencias más altas, al mismo tiempo que se oscurecen las zonas de frecuencias bajas. Es común la aparición de ruido tras el proceso.
Realce de bordes por desplazamiento y diferencia: sustrae de la imagen original una copia desplazada de la misma. Así, es posible localizar y hacer resaltar los bordes existentes y que se quieran obtener según el modelo de núcleo aplicado:
- Horizontal.
- Vertical.
- Horizontal/Vertical (diagonal).

Realce de bordes mediante Laplace: este tipo de filtros realza los bordes en todas direcciones (los resultados que se obtienen pueden considerarse como una “suma” de los obtenidos tras aplicar todos los modelos del tipo anterior). En esta ocasión se trabaja con la segunda derivada, que permite obtener unos mejores resultados, a pesar del aumento del ruido que se produce en la imagen.
Resalte de bordes con gradiente direccional: empleado para destacar y resaltar con mayor precisión los bordes que se localizan en una dirección determinada. Trabaja con los cambios de intensidad existentes entre píxeles contiguos.
Detección de bordes y filtros de contorno (Prewitt y Sobel): al igual que los anteriores, se centra en las diferencias de intensidad que se dan pixel a pixel. Son utilizados para obtener los contornos de objetos y de este modo clasificar las formas existentes dentro de una imagen. Este tipo de filtros requieren un menor coste computacional.

Tratamiento de imagen por procesamiento de punto

Se trata de la mejora de la imagen considerando los métodos de procesamiento que se basan solo en la intensidad de píxeles individuales. En lo que sigue llamaremos r y s a la intensidad de los píxeles antes y después del procesado. A continuación se presentan ejemplos de tratamiento de imagen por procesamiento de punto utilizando el software de acceso libre ImageJ:

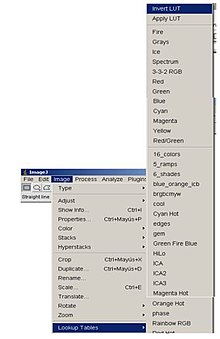
-Negativos de imágenes: La idea de esta transformación es invertir el orden de blanco a negro, de forma que la intensidad de la imagen de salida disminuya conforme la intensidad de la imagen de entrada aumente. Mediante ImageJ es sencillo realizar el negativo de una imagen. Esta se conseguiría a partir de la lookup table, Invert LUT.

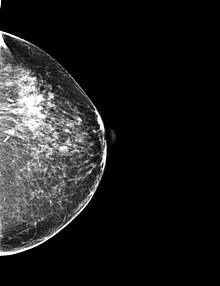
Imagen original	Negativo de la imagen

-Aumento del contraste:

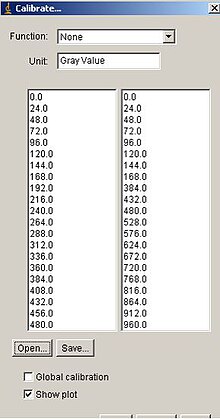
La idea del aumento de contraste consiste en incrementar el rango dinámico de los niveles de gris de la imagen que se está procesando. La ubicación de los puntos (r1,s1) y (r2,s2) controla la forma de la función de transformación.

A partir de la opción "Calibrate" del ImageJ , diseño la función de transformación siguiente que me permite incrementar el contraste de la imagen original.

Imagen original mamografía		Imagen contrastada

-Compresión del rango dinámico: Puede ocurrir que el rango dinámico de una imagen procesada excede la capacidad del dispositivo de presentación por lo que solo veremos las partes más brillantes de la imagen. Una manera de comprimir el rango dinámico en realizar una transformación de este tipo:

s=C·log(1+| r | )

Utilizando de nuevo el ImageJ, podemos diseñar una función de la forma anterior que nos permita comprimir el rango dinámico de una imagen. En este caso se ha utilizado el Plugin "Expresion NT" , definiendo una función de la forma:

s=100.log(1+| r | )

Imagen original		Imagen después de transformación

-Fraccionamiento del nivel de gris: Si se desea destacar un rango específico del nivel de gris de una imagen. se puede por ejemplo adjudicar un valor alto a todos aquellos niveles de gris del rango de interés y uno bajo a los restantes.

-Fraccionamiento de los planos de bits: A veces puede desearse destacar la contribución que realizan a la imagen determinados bits específicos en vez de un rango determinado, es lo que se consigue con esta transformación.

Interpolación

El proceso de interpolación está relacionado con el hecho de desear cambiar la tasa de muestreo de una señal discreta a una tasa menor o mayor con la que fue muestreada originalmente. El proceso con el cual se disminuye la tasa de muestreo de una señal discreta por un factor D se denomina decimación o submuestreo (downsampling) y el proceso con el cual se aumenta la tasa de muestreo de una señal discreta por un factor T se denomina interpolación (upsampling).

El orden del filtro indicará como se aproxima a través de un polinomio a la función representada por las muestras. Existen muchos filtros interpoladores y en el caso de imágenes estos se obtienen discretizando, en los valores deseados, los polinomios interpoladores. Los polinomios interpoladores utilizados frecuentemente son: líneas, cúbicos o bicúbicos. Un interpolador de orden cero básicamente efectúa un zoom duplicado. Un interpolador de orden lineal efectúa un zoom asignando el promedio de dos muestras a la muestra interpolada.

Existe también otro método de interpolación y es que se realiza en el dominio de la frecuencia. Uno de los principales fundamentos de las señales discretas es que el “zero padding” en un dominio resulta en un incremento de la tasa de muestreo en el otro dominio.

Acercamientos recientes

A partir de los avances en la computación cuántica, ha surgido una aplicación al procesamiento digital de imágenes denominado como procesamiento cuántico de imágenes, quantum image processing en inglés y abreviado como QIMP, que aún se encuentra en etapas iniciales de investigación y cuya mayor interrogante es cómo representar una imagen digital tradicional en un computador cuántico,^[1]el cual procesa la información mediante cubits de la forma:

$|\psi \rangle =\alpha |0\rangle +\beta |1\rangle$

donde ${\textstyle |0\rangle ={\begin{pmatrix}1\\0\end{pmatrix}}}$ , ${\textstyle |1\rangle ={\begin{pmatrix}0\\1\end{pmatrix}}}$ y ${\textstyle \alpha }$ y ${\textstyle \beta }$ son amplitudes que satisfacen ${\textstyle \left|\alpha \right|^{2}+\left|\beta \right|^{2}=1}$ ^[1]

De los diferentes acercamientos para representar una imagen en un computador cuántico, se encuentra FRQI (Flexible Representation for Quantum Images), que captura la posición y el color de cada pixel dentro de un estado cúantico,^[2]de la forma:

$|I\rangle ={\frac {1}{2^{n}}}\sum _{i=0}^{2^{2n-1}}|c_{i}\rangle \otimes |i\rangle$

donde ${\textstyle |i\rangle }$ representa la posición y ${\textstyle |c_{i}\rangle =cos\theta _{i}|0\rangle +sin\theta _{i}|1\rangle }$ el color con un vector de ángulos ${\textstyle \theta _{i}\in \left[0,\pi /2\right]}$ ^[2]

Véase también

Matlab, software matemático que permite realizar procesamiento digital de imágenes.
Visión por computadora
Base de datos MNIST

Referencias

↑ ^a ^b Yan, Fei; Venegas-Andraca, Salvador E. (2020). Introduction and Overview (en inglés). Springer Singapore. pp. 1-17. ISBN 978-981-329-330-4. doi:10.1007/978-981-32-9331-1_1. Consultado el 30 de octubre de 2024.
↑ ^a ^b Yan, Fei; Venegas-Andraca, Salvador E. (2020). Quantum Image Representations (en inglés). Springer Singapore. pp. 19-48. ISBN 978-981-329-330-4. doi:10.1007/978-981-32-9331-1_2. Consultado el 30 de octubre de 2024.

Bibliografía

González, R.C., Wintz, P. (1996). Procesamiento digital de imágenes. Addison-Wesley.
Acharya, T., Ray, A. K. (2005). Image processing: principles and applications. John Wiley & Sons.
Alegre, E., Sánchez, L., Fernández, R. Á., Mostaza, J. C. (2003). Procesamiento Digital de Imagen: fundamentos y prácticas con Matlab. Universidad de León. ISBN 84-9773-052-6.
Rafael C. González, Richard E. Woods, Steven L. Eddins (2009). Digital image processing using Matlab. González, Woods, & Eddins.

Enlaces externos

Datos: Q1070689
Multimedia: Digital image processing / Q1070689

[:0-1] Yan, Fei; Venegas-Andraca, Salvador E. (2020). Introduction and Overview (en inglés). Springer Singapore. pp. 1-17. ISBN 978-981-329-330-4. doi:10.1007/978-981-32-9331-1_1. Consultado el 30 de octubre de 2024.

[:1-2] Yan, Fei; Venegas-Andraca, Salvador E. (2020). Quantum Image Representations (en inglés). Springer Singapore. pp. 19-48. ISBN 978-981-329-330-4. doi:10.1007/978-981-32-9331-1_2. Consultado el 30 de octubre de 2024.

[1]

[2]