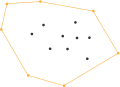
Quickhull

Quickhull
Ejecución paso a paso del algoritmo Quickhull
Tipo	Algoritmo Geométrico
Problema que resuelve	Cierre convexo
Creador	Barber, Dobkin y Huhdanpaa[1]​
Fecha	1996
Clase de complejidad	P
Tiempo de ejecución
Peor caso	${\displaystyle O(n^{2})\,}$
Caso promedio	${\displaystyle O(n\log n)\,}$
[editar datos en Wikidata]

Quickhull es un método para calcular el cierre convexo de un conjunto finito de puntos (generalmente en el plano 2D, pero también existen versiones para dimensiones superiores). Emplea una técnica basada en divide y vencerás similar a la empleada por el algoritmo de ordenación quicksort, del que toma su nombre.^[1]​

Su complejidad promedio es Θ(n * log(n)), aunque en el peor caso puede tomar O(n²) en situaciones de alta simetría o con conjuntos de puntos situados en forma de circunferencia.

Algoritmo

La versión en 2D del algoritmo Quickhull puede dividirse en los siguiente pasos:

1. Buscar un par de puntos optimales, generalmente los puntos con menor y mayor coordenada X, ya que estos siempre forman parte del cierre convexo.
2. Usar la línea entre ambos puntos para dividir el conjunto en dos subconjuntos que serán procesador de forma recursiva.
3. Determinar el punto situado a mayor distancia de la línea anterior. Junto a los dos puntos anteriores, formará un triángulo.
4. Todos los puntos situados en el interior del triángulo pueden ser descartados, ya que no formarán parte del cierre convexo.
5. Repetir los dos pasos anteriores en los dos lados del triángulo (no en el lado inicial).
6. Repetir hasta que no queden puntos sin clasificar. Los puntos seleccionados forman el cierre convexo..

• 
  Pasos 1-2: Dividir los puntos en dos subconjuntos mediante una línea.
• 
  Paso 3: Buscar el punto a mayor distancia y formar un triángulo.
• 
  Paso 4: Descartar los puntos interiores al triángulo.
• 
  Paso 5: Repetir la clasificación empleando los dos nuevos lados del triángulo.
• 
  Paso 6: Resultado final.

Implementaciones públicas

Los autores del algoritmo mantienen una implementación del algoritmo mediante una librería en lenguaje C que puede ser llamada desde varios lenguajes (como C++, Python). El código puede descargarse desde la página del proyecto www.qhull.org o desde su repositorio de GitHub

Referencias y enlaces externos

1. Barber, C. Bradford; Dobkin, David P.; Huhdanpaa, Hannu (1 de diciembre de 1996). «The quickhull algorithm for convex hulls». ACM Transactions on Mathematical Software 22 (4): 469-483. doi:10.1145/235815.235821. 

• Dave Mount. «QHull.org code for Convex Hull, Delaunay Triangulation, Voronoi Diagram, and Halfspace Intersection about a Point.». 
• Dave Mount. «Lecture 3: More Convex Hull Algorithms». Archivado desde el original el 10 de junio de 2018. Consultado el 6 de julio de 2018. 
• Joseph O'Rourke (1998). Computational Geometry in C (2nd edición). Cambridge University Press. ISBN 0-521-64976-5. 
• Pseudocódigo, "https://web.archive.org/web/20180627005540/http://www.cse.yorku.ca/~aaw/Hang/quick_hull/Algorithm.html".
• Implementing QuickHull (GDC 2014) – Algorithm presentation with 3D implementation details.