Sangaku

Para otros usos de este término, véase Sangaku (música).

Sangaku

Sexteto de Soddy, en una tablilla sangaku

Sangaku o San Gaku (算額, lit. Tablilla Matemática^?) son tablillas de origen japonés con problemas matemáticos principalmente geométricos, creadas durante el período Edo.

Un sangaku es una tablilla de madera con figuras geométricas, ubicadas en los templos y santuarios como ofrendas votivas a los dioses o como desafíos a los congregados y visitantes, escritos en kanbun, una forma antigua de japonés. Cada tablilla sangaku contiene entre 1 y 10 problemas, y cada problema está formado de la siguiente manera: arriba (o a la derecha) de la tablilla se ubican las figuras geométricas; abajo (o a la izquierda) se encuentran la pregunta y soluciones (procedimiento, respuesta, o ambas si las hay); y por último el creador del sangaku, el profesor, la escuela y la fecha de su colgado.

Historia

Templo japonés ( Kioto).

Los sangaku provienen de la costumbre nipona de colgar tablillas en los templos, originada por el sintoísmo (del japonés Shinto (神道, shintō^?). El sintoismo o shintoísmo afirma la existencia de divinidades o seres espirituales (Kami (神, Kami^?)) que pueden encontrarse en la naturaleza o en niveles superiores de existencia. Este término, que constituye el concepto central del culto, se aplica a cualquier fuerza sobrenatural o dios, como los dioses de la naturaleza, hombres sobresalientes, antepasados deificados o hasta deidades que representan ciertos ideales o simbolizan un poder abstracto. Se trata de vivir en armonía con los kami, y así poder disfrutar de su protección y aprobación. Y dado que a los kami les encantan los caballos vivos, los fieles que no podían ofrendar un caballo, tenían la opción de ofrecer un remado en madera. Es por esto que muchas tablillas que datan del siglo XV o antes, contienen representaciones de caballos.^[1]​^[2]​

El periodo Edo fue un periodo de paz que duró cerca de dos siglos y medio. Antes de ese momento el país había sido devastado por una serie de guerras internas provocadas por los distintos clanes rivales que querían llegar al poder. Hasta que finalmente el orden fue restablecido por el shogun que es la máxima autoridad después del emperador, tokugawa leyasu, llevó a cabo la reunificación del país tanto política como económica, fue así como la capital fue trasladada de Kioto a Edo, desde ese momento Japón llevó un aislamiento voluntario con respecto al resto del mundo, y todo aquel que se atreviese a desobedecer esto, era condenado a muerte, fue así como que en 1854 el gobierno fue derrocado por la fuerza naval norteamericana. Este periodo de aislamiento también produjo que las matemáticas avanzaran mucho en Japón ya que no tenían acceso al resto del mundo, fueron las mismas personas tanto campesinos como samuráis quienes dieron un desarrollo genuino a este periodo.

Muchas de estas tablillas se perdieron durante el período de modernización que siguió al período Edo, de las 2625 tablillas que se supone existieron, 884 se conservan.^[3]​ La tablilla Sangaku más antigua que se conoce proviene de la prefectura de Tochigi y se remonta a 1683. Aunque el diario del matemático japonés Kazu Yamagushi (1781-1850) se alude a una tablilla del año 1668, perdida en la actualidad.^[1]​

Fujita Kagen (1765-1821), matemático japonés, publicó la primera colección de problemas Sangaku, en sus obras Shinpeki Sanpō (Problemas matemáticos suspendidos en el Templo) en 1789, y una segunda parte en 1806, Zoku Shinpeki Sanpō. Una colección de Sangaku fue publicada en 1989 por Hidetoshi Fukagawa y Daniel Pedoe, la primera en inglés, en el libro: Japanese Temple Geometry Problems.

Aspectos matemáticos

El teorema de Pitágoras es la herramienta más utilizada en la resolución de los problemas sangaku (Chou Pei Suan Ching, 500-200 a. C.).

Sobre los temas en los que se enfocan los Sangaku, son principalmente la geometría euclidiana y específicamente sobre círculos, elipses, esferas, cuadrados, rectángulos, cilindros, triángulos, conos, cubos, figuras dentro de otras figuras, como también el cálculo de volumen de diversos sólidos, requiriendo de cálculo integral. Sobre temas algebraicos se encuentran los sistemas de ecuaciones, interés simple-compuesto, ecuaciones diofánticas simples.^[4]​

Gran parte de los problemas entrarían en la categoría de matemática recreativa, pero algunos usan versiones japonesas de algunos teoremas como el teorema de los círculos de Descartes, mientras otros se adelantan a famosos resultados occidentales como el teorema de Malfatti, el teorema de Casey o el sexteto de Soddy.^[5]​

Algunos de los problemas son sencillos y solo se requiere de conocimientos de secundaria como el teorema de Pitágoras y semejanza de triángulos, mientras otros requieren de matemáticas superiores para ser abordados como el enri (cálculo integral japonés) y derivadas

Problemas sangaku

Problema sangaku con un triángulo isósceles y dos círculos.

Un círculo que contiene a dos círculos, un triángulo isósceles y una perpendicular

En este problema de la Prefectura de Gunma de 1803, la base del triángulo isósceles descansa sobre el diámetro de la circunferencia mayor. El centro de la circunferencia azul se encuentra en el diámetro de la circunferencia amarilla y la circunferencia es tangente interior a la circunferencia amarilla. La circunferencia verde es tangente exterior del triángulo y de la circunferencia azul, e interior de la circunferencia amarilla. Hay que demostrar que el segmento que conecta el centro de la circunferencia verde con el punto de intersección del triángulo y la circunferencia azul es perpendicular con el diámetro de la circunferencia amarilla.

En la solución dada en el sangaku, el autor traza un segundo segmento rectilíneo distinto del segmento enunciado que pasa por el centro del círculo verde y que es perpendicular al diámetro del círculo amarillo, de modo que los dos segmentos deberían interceptar al diámetro en puntos distintos. Luego, se demuestra que la distancia entre estos dos puntos tiene que ser necesariamente cero lo que supone que estos segmentos son idénticos, demostrando la perpendicularidad.

Problema Sangaku de la prefectura de Gumma del año 1824.

Tres circunferencias tangentes entre sí y a una recta

Este problema de la Prefectura de Gunma del año 1824, trata sobre tres circunferencias tangentes entre sí y a una misma recta. Se pide determinar el radio de la circunferencia más pequeña en términos de las dos circunferencias restantes. La solución a este problema es:

${\displaystyle {\frac {1}{\sqrt {r_{1}}}}={\frac {1}{\sqrt {r_{2}}}}+{\frac {1}{\sqrt {r_{3}}}}}$

o

${\displaystyle r_{1}={\frac {r_{2}r_{3}}{({\sqrt {r_{2}}}+{\sqrt {r_{3}}})^{2}}}}$

donde r₁, r₂, r₃ son respectivamente el radio de la circunferencia rojo, verde y azul. Este problema es un caso especial del teorema de los círculos de Descartes cuando la cuarta circunferencia tiene curvatura cero. Puede resolverse aplicando el teorema de Pitágoras.

Primer Teorema japonés

Segundo teorema japonés.

Primer Teorema de Mikami-Kobayashi

También llamado Primer Teorema japonés, este teorema nos dice que al triangular un polígono convexo inscrito en un círculo, mediante diagonales que no se intersequen en el interior del polígono, la suma de los radios de los círculos inscritos en los triángulos es una constante (invariante) que es independiente de la triangulación elegida. El número de triangulaciomes posibles de un polígono de n lados es ${\displaystyle Cat(n-2)}$, el número ${\displaystyle n-2}$ de Catalan, donde ${\displaystyle Cat(n)={\frac {\binom {2n}{n}}{n+1}}}$.

En la imagen se muestran dos triangulaciones de un hexágono inscrito, formando las circunferencias verdes y azules respectivamente. Por el primer teorema japonés:

La suma de los radios de las circunferencias verdes

=

suma de los radios de las circunferencias azules

La idea básica de la prueba es utilizar el teorema de Carnot en cada triángulo inscrito en el polígono.

Segundo teorema de Mikami-Kobayashi

También llamado Segundo teorema japonés, este teorema nos dice que al unir los incentros de los triángulos formados al trazar las diagonales de un cuadrilátero inscrito en una circunferencia se forma un rectángulo.

Sea ${\displaystyle \square ABCD}$ un cuadrilátero y ${\displaystyle M_{1},M_{2},M_{3},M_{4}}$ los incentros de los triángulos ${\displaystyle \triangle ABD,\triangle ABC,\triangle BCD,\triangle ACD}$. Entonces el cuadrilátero formado por ${\displaystyle M_{1},M_{2},M_{3},M_{4}}$ es un rectángulo.

La idea básica de la demostración es probar que los ángulos del cuadrilátero formado por los incentros son rectos y por lo tanto es un rectángulo.

Sexteto de Soddy japonés.

Sexteto de Soddy

Artículo principal: Sexteto de Soddy

Este problema de la prefectura de Kanagawa de 1822 colgado en el santuario de Kōzagun por Yazawa Hiroatsu, se anticipa en más de cien años al trabajo de Frederick Soddy. Dos esferas tangentes A y B entre sí están inscritas en una gran esfera C. El problema es determinar el número de esferas que forman el collar, o sea, esferas de distintos tamaños tangentes a sus dos vecinos más cercanos y a las tres esferas dadas, además se pide encontrar los radios de las esferas que forman el collar en función de los radios de A, B y C.

La solución viene dada por el teorema del sexteto de Soddy (1937) que nos dice que habrá solo 6 esferas. La solución usando wasan del manuscrito Sanpō Tenzan Tebikigusa (1841) de Ōmura Kazuhide (1824–1891), aplica la versión japonesa del teorema de los círculos de Descartes como idea básica y la extiende al mundo de las esferas.

Sangakus algebraicos

Entre los sangakus algebraicos destacan:

• El problema de la tablilla de Ufa Chusaburō de 1743: Se tienen 50 pollos y conejos. Si el número de patas es 122, ¿Cuántos pollos y conejos hay?.
• De la tablilla del templo Shōganji, prefectura de Nagano: Se divide un capital de 60 en forma igualitaria para repartir a varios hombres como préstamo a interés compuesto por más de 3 años, después del cual el capital de vuelta con interés añadido será 105.12. La diferencia de la tasa de interés anual entre cada deudor es de 10% y la suma de la tasa de interés anual es de 60%. Encontrar el número de hombres a los cuales se les ha dado el préstamo.
• Del santuario Hioki-jinja: Se tienen dos cubos, A (el más grande) y B. La suma de los volúmenes de A y B es 2240 sun (80499 cm³) y la diferencia entre los lados de A y B es 4 sun (13.2 cm). Encontrar la longitud del lado de B.

Algunas soluciones

Tres circunferencias tangentes entre sí y a una recta

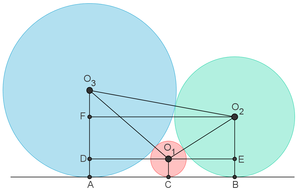
Sean las longitudes de los segmentos
${\displaystyle O_{2}O_{3}=r_{2}+r_{3}\;}$ ,
${\displaystyle O_{1}O_{2}=r_{1}+r_{2}\;}$ y
${\displaystyle O_{1}O_{3}=r_{1}+r_{3}\,}$,que conectan los centros de las circunferencias.

Luego, los segmentos ${\displaystyle AB}$ y ${\displaystyle FO_{2}}$ tienen igual longitud y por Teorema de Pitágoras : ${\displaystyle AB=FO_{2}={\sqrt {(O_{2}O_{3})^{2}-(O_{3}F)^{2}}}={\sqrt {(r_{2}+r_{3})^{2}-(r_{3}-r_{2})^{2}}}=2{\sqrt {r_{2}r_{3}}}}$ ; de forma análoga para los segmentos ${\displaystyle AC=DO_{1}=2{\sqrt {r_{1}r_{3}}}}$ y ${\displaystyle CB=EO_{1}=2{\sqrt {r_{2}r_{1}}}}$.

Como ${\displaystyle AB=AC+CB\,}$, tenemos que: ${\displaystyle 2{\sqrt {r_{2}r_{3}}}=2{\sqrt {r_{1}r_{3}}}+2{\sqrt {r_{1}r_{2}}}}$ dividiendo por ${\displaystyle 2{\sqrt {r_{1}r_{2}r_{3}}}}$ a ambos lados de la ecuación se llega a la solución.

Resolución del problema de la Prefectura de Gunma.

Resolución gráfica

El problema gráfico se soluciona usando las propiedades de la Inversión. Generalmente los problemas de tangencias de dos circunferencias y una recta se reducen al de una circunferencia, una recta y un punto restando a cada elemento el radio de la circunferencia menor. El problema suele tener cuatro soluciones que aquí es solo una.

Una vez reducido, dibujamos una recta que pase por el centro de la circunferencia y sea perpendicular a la recta y hacemos que el punto más alejado (C) sea el centro de una inversión en la que la recta sea la figura inversa de la circunferencia, y el punto A sea inverso de B. La circunferencia de centro 03, que contiene los puntos A, B y O2, nos permite hallar el inverso de éste, O2’. Prolongando la recta común a estos dos puntos hallamos sobre la recta el centro radical CR. (Figura 2)

El centro radical nos da el punto de tangencia T, y la mediatriz de los puntos inversos O2 nos da el centro de la solución buscada, la circunferencia tangente a la recta r’, la circunferencia reducida de centro O1 y el punto O2. (Figura 3)

Este centro es también el de la circunferencia buscada en el sangaku. (Figura 4)

Primer Teorema de Mikami-Kobayashi

Consideremos la triangulación de un 5-polígono convexo inscrito en una circunferencia de radio R. Sean m₁, . . . ,m₅ los segmentos de mediatrices (o simetrales) desde el circuncentro a los lados. Sean r₁, r₂ y r₃ los radios de las circunferencias inscritas en los triángulos ΔABC, ΔACD y ΔADE respectivamente. Aplicando el teorema de Carnot a estos triángulos obtenemos:

${\displaystyle m_{1}+m_{2}-m_{y}=R+r_{1}\;}$

${\displaystyle m_{3}+m_{x}+m_{y}=R+r_{2}\;}$

${\displaystyle m_{4}+m_{5}-m_{x}=R+r_{3}\;}$

Sumando miembro a miembro, conmutando y despejando los radios obtenemos:

${\displaystyle r_{1}+r_{2}+r_{3}=(m_{1}+m_{2}+m_{3}+m_{4}+m_{5})-3R\;}$

El miembro derecho de la igualdad no depende de la triangulación que hemos utilizado. De forma análoga se puede probar para cualquier k-polígono convexo.

Referencias

1. Rothman Tony; Fukagawa Hidetoshi (1998). «Geometría en los templos de Japón». Investigación y Ciencia (julio). pag. 72-79. Archivado desde el original el 25 de diciembre de 2009. Consultado el 22 de agosto de 2008. 
2. Rehmeyer, Julie (2008). «Science News / Sacred Geometry : Sacred Geometry». Consultado el 2008.  La referencia utiliza el parámetro obsoleto |añoacceso= (ayuda)
3. Itō,E.;Nomura, E.; Tanaka, H.; Kobayashi, H.; Kitahara, I.; Ōtani, K.; Nakamura, N.; Yanagisawa, R.; Sekiguchi, T. (2003). Japanese Temple Mathematical Problems. Japón: Kyōikushokan,. 
4. Fouz, Fernando (2003). «Sangaku: Geometría en los Templos Japoneses.». Revista Sigma (22). pag. 173-190. 
5. Miranda, Ubaldo (2002). «Sangaku». Archivado desde el original el 9 de junio de 2007. Consultado el 2008.  La referencia utiliza el parámetro obsoleto |añoacceso= (ayuda)

Libros

• Fukagawa, Hidetoshi ; Pedoe, Daniel (1989) Japanese Temple Geometry Problems: Sangaku. Charles Babbage Research Centre. ISBN 0-919611-21-4.
• Fukagawa, Hidetoshi ; Rothman, Tonny (2008) Sacred Mathematics: Japanese Temple Geometry. Princeton University Press, Princeton. ISBN 0-691-12745-X.
• Huvent, Géry (2008) Sangaku. Le mystère des énigmes géométriques japonaises, Dunod. ISBN 2-10-052030-X

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre Sangaku.

Problemas sangaku

• García Capitán, F. J. (2003) Problemas sangaku
• Miranda, Ubaldo(2003). Gacetilla Matemática: Apuntes y notas sobre problemas sangakus
• Parra, C.(2005) TÍPICOS PROBLEMAS SANGAKUS.
• Martin, M.(2008) Sangakus.
• Gutiérrez, Antonio(2007). Geometry step-by-step:Sangaku Japanese Geometrical problem: The incenters of four triangles in a cyclic quadrilateral - Antonio Gutiérrez. Una demostración interactiva sobre un problema Sangaku.
• Larrosa Cañestro, I. (2013) Teorema Japonés

Otros sitios

• Aprendiendo Geometría a través de Sangaku (enlace roto disponible en Internet Archive; véase el historial, la primera versión y la última).
• Delerue, Nicolas. Sangaku (Japanese votive tablets featuring mathematical puzzles)
• Wasan.jp. ようこそ算額のホームページへ Catálogo de Sangaku, según prefectura de origen.
• Bogomolny, Alexander. «Sangaku: Reflections on the Phenomenon». Interactive Mathematics Miscellany and Puzzles (en inglés). 
• Huvent, Géry http://pagesperso-orange.fr/gery.huvent/html/sangaku.htm