Sólidos arquimedianos

Los sólidos arquimedianos o sólidos de Arquímedes son un grupo de 13 poliedros convexos cuyas caras son polígonos regulares de dos o más tipos. Todos los sólidos de Arquímedes son de vértices uniformes. La mayoría de ellos se obtienen por truncamiento de los sólidos platónicos. Arquímedes describió extensamente estos cuerpos en trabajos que se fueron perdiendo, y que en el Renacimiento fueron redescubiertos por artistas y matemáticos.

Siete sólidos arquimedianos se pueden obtener truncando sólidos platónicos:

Los dos rombicuboctaedros se pueden obtener a partir del cuboctaedro mediante sucesivas operaciones de truncamiento y desplazamiento radial de las caras. De forma similar, los dos rombicosidodecaedros se pueden obtener a partir del icosidodecaedro mediante sucesivas operaciones de truncamiento y desplazamiento radial de las caras.

Las dos formas enantiomorfas del cuboctaedro romo se pueden obtener a partir del rombicuboctaedro menor mediante una transformación más compleja que incluye una rotación coordinada de los cuadrados paralelos a los originales del cubo, de los triángulos que los conectan por sus vértices y, simultáneamente, la conversión de cada uno de los cuadrados que los conectan por las aristas en dos triángulos equiláteros. El sentido de la rotación de los cuadrados determina la orientación del sólido resultante.

De forma similar, las dos formas enantiomorfas del icosidodecaedro romo se pueden obtener a partir del rombicosidodecaedro menor mediante una rotación coordinada de los pentágonos paralelos a los originales del dodecaedro, de los triángulos que los conectan por sus vértices y, simultáneamente, la conversión de cada uno de los cuadrados que los conectan por las aristas en dos triángulos equiláteros. El sentido de la rotación de los pentágonos determina la orientación del sólido resultante.

El cuboctaedro es el caso límite coincidente del truncamiento del cubo y del octaedro. De forma similar, el icosidodecaedro es el caso límite coincidente del truncamiento del dodecaedro y del icosaedro. Ambos son los únicos sólidos arquimedianos cuyas aristas son uniformes, por lo que se consideran sólidos semirregulares.

Dado que en los vértices de los sólidos arquimedianos se encuentran varios tipos de polígonos se ha buscado una manera de nombrar la forma de los vértices; se dice por ejemplo que un vértice tiene configuración 3.5.5 cuando en el vértice se encuentran un triángulo y dos pentágonos, como en el icosidodecaedro. Este sistema se aplica también para las demás familias de poliedros.

Sólidos arquimedianos
Número de Sólido Nombre Imagen Caras Aristas Vértices Grupo puntual
1 Tetraedro truncado
Animación 		8 4 × {6}
4 × {3} 		18 12 × 3.6.6 Td
2 Cuboctaedro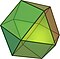
Animación 		14 6 × {4}
8 × {3} 		24 12 × 3.4.3.4 Oh
3 Cubo truncado
Animación 		14 6 × {8}
8 × {3} 		36 24 × 3.8.8 Oh
4 Octaedro truncado
Animación 		14 8 × {6}
6 × {4} 		36 24 × 4.6.6 Oh
5 Rombicuboctaedro o rombicuboctaedro menor
Animación 		26 18 × {4}
8 × {3} 		48 24 × 3.4.4.4 Oh
6 Cuboctaedro truncado o rombicuboctaedro mayor
Animación 		26 6 × {8}
8 × {6}
12 × {4} 		72 48 × 4.6.8 Oh
7 Cubo romo o cuboctaedro romo
(2 formas enantiomorfas)
Animación

Animación 		38 6 × {4}
32 × {3} 		60 24 × 3.3.3.3.4 O
8 Icosidodecaedro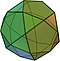
Animación 		32 12 × {5}
20 × {3} 		60 30 × 3.5.3.5 Ih
9 Dodecaedro truncado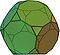
Animación 		32 12 × {10}
20 × {3} 		90 60 × 3.10.10 Ih
10 Icosaedro truncado
Animación 		32 20 × {6}
12 × {5} 		90 60 × 5.6.6 Ih
11 Rombicosidodecaedro
o rombicosidodecaedro menor
Animación 		62 12 × {5}
30 × {4}
20 × {3} 		120 60 × 3.4.5.4 Ih
12 Icosidodecaedro truncado o rombicosidodecaedro mayor Animación 62 30 × {4}
20 × {6}
12 × {10} 		180 120 × 4.6.10 Ih
13 Dodecaedro romo o icosidodecaedro romo
(2 formas enantiomorfas) 		Animación

Animación

92 12 × {5}
80 × {3} 		150 60 × 3.3.3.3.5 Ih

Véase también

[editar]

Bibliografía

[editar]