Teoría del forrajeo óptimo

Las abejas obreras buscan el néctar no solo para ellas mismas, sino para toda su comunidad colmena. La teoría del forrajeo óptimo predice que esta abeja se alimentará de una manera que maximice el rendimiento neto de energía de su colmena.

La teoría del forrajeo óptimo (TFO) es un modelo ecológico de comportamiento que ayuda a predecir cómo se comporta un animal cuando busca comida. Si bien la obtención de alimentos proporciona energía al animal, la búsqueda y la captura de los mismos requieren energía y tiempo. Para maximizar la condición física, un animal adopta una estrategia de forrajeo que proporciona el mayor beneficio (energía) al menor costo, maximizando la energía neta obtenida. OFT ayuda a predecir la mejor estrategia que un animal puede usar para lograr este objetivo. La palabra forrajeo no es aceptada por la Real Academia Española, sin embargo el verbo forrajear, sí lo está. Este se define como "segar y recoger el forraje“ por lo que la comunidad científica ha adoptado este concepto. El término forrajeo es usado en publicaciones científicas.^[1]​ Alternativamente se puede sustituir por "búsqueda de alimento"^[2]​ o en este caso la Teoría de la búsqueda de alimento óptima.

Figura 1. Ganancia de energía por costo (E) para adoptar estrategia de forraje x. Adaptado de Parker Y Smith.^[3]​

Modelo de forrajeo óptimo.

La TFO es una aplicación ecológica del modelo de optimalidad. Esta teoría asume que el patrón de alimentación más ventajoso económicamente se seleccionará en una especie a través de selección natural.^[4]​ Cuando se usa la TFO para modelar el comportamiento de forrajeo, se dice que los organismos maximizan una variable conocida como la moneda, como la mayor cantidad de alimentos por unidad de tiempo. Además, las restricciones del entorno son otras variables que deben ser consideradas. Las restricciones se definen como factores que pueden limitar la capacidad del forrajero para maximizar la moneda. La regla de decisión óptima, o la mejor estrategia de forrajeo del organismo, se define como la decisión que maximiza la moneda bajo las limitaciones del entorno. Identificar la regla de decisión óptima es el objetivo principal de la TFO.^[5]​

Tigre (Panthera tigris). Ejemplo de depredador

Un modelo de alimentación óptimo genera predicciones cuantitativas de cómo los animales maximizan su condición física mientras forrajean. El proceso de creación del modelo implica la identificación de la moneda, las restricciones y la regla de decisión adecuada para el forrajero.^[6]​

La moneda se define como la unidad optimizada por el animal. También es una hipótesis de los costos y beneficios que se imponen a ese animal.^[7]​ Por ejemplo, un determinado forraje obtiene energía de los alimentos, pero incurre en el costo de buscar el alimento: el tiempo y la energía gastados en la búsqueda podrían haberse utilizado en otros esfuerzos, como buscar parejas o proteger a los jóvenes. Sería el mejor interés del animal maximizar sus beneficios al menor costo. Por lo tanto, la moneda en esta situación podría definirse como la ganancia de energía neta por unidad de tiempo.^[8]​

Sin embargo, para un forrajero diferente, el tiempo que lleva digerir los alimentos después de comerlos puede ser un costo más significativo que el tiempo y la energía gastados en buscarlos. En este caso, la moneda podría definirse como la ganancia de energía neta por tiempo de rotación digestiva en lugar de la ganancia de energía neta por unidad de tiempo.^[9]​ Además, los beneficios y los costos pueden depender de la comunidad de un forrajero. Por ejemplo, un forrajero que vive en una colmena probablemente forrajearía de una manera que maximizaría la eficiencia de su colonia en lugar de la de ella misma.^[7]​ Al identificar la moneda, se puede construir una hipótesis sobre qué beneficios y costos son importantes para el forrajero en cuestión.

Las restricciones son hipótesis sobre las limitaciones que se colocan en un animal. Estas limitaciones pueden deberse a las características del entorno o la fisiología del animal y podrían limitar su eficiencia de forrajeo. El tiempo que tarda el forrajeador en viajar desde el sitio de anidación al sitio de forrajeo es un ejemplo de una restricción. El número máximo de alimentos que un forrajero puede transportar a su sitio de anidación es otro ejemplo de una restricción. También podría haber restricciones cognitivas en los animales, como los límites al aprendizaje y la memoria.^[8]​ Cuantas más restricciones se puedan identificar en un sistema dado, más poder predictivo tendrá el modelo.^[7]​

Mosquito (Aedes aegypti). Ejemplo de pastor

Dadas las hipótesis sobre la moneda y las restricciones, la regla de decisión óptima es la predicción del modelo de cuál debería ser la mejor estrategia de forrajeo del animal.^[8]​ Los posibles ejemplos de reglas de decisión óptimas podrían ser el número óptimo de alimentos que un animal debería llevar a su sitio de anidación o el tamaño óptimo de un alimento en el que un animal debería alimentarse. La Figura 1 muestra un ejemplo de cómo se puede determinar una regla de decisión óptima a partir de un modelo gráfico. La curva representa la ganancia de energía por costo (E) para adoptar la estrategia de forrajeo x. La ganancia de energía por costo es la moneda que se optimiza. Las restricciones del sistema determinan la forma de esta curva. La regla de decisión óptima (x *) es la estrategia para la cual la divisa, la ganancia de energía por costo, es la mayor. Los modelos óptimos de alimentación pueden parecer muy diferentes y volverse muy complejos, dependiendo de la naturaleza de la moneda y la cantidad de restricciones consideradas. Sin embargo, los principios generales de moneda, restricciones y regla de decisión óptima siguen siendo los mismos para todos los modelos.

Para probar un modelo, uno puede comparar la estrategia predicha con el comportamiento real de alimentación del animal. Si el modelo se ajusta bien a los datos observados, entonces se admiten las hipótesis sobre la moneda y las restricciones. Si el modelo no se ajusta bien a los datos, es posible que se haya identificado incorrectamente la moneda o una restricción en particular.^[7]​

Diferentes sistemas de alimentación y clases de depredadores.

Mildiu de la patata. Ejemplo de parásito

La teoría del forrajeo óptimo es ampliamente aplicable a los sistemas de alimentación en todo el reino animal. Bajo la TFO, cualquier organismo de interés puede ser visto como un depredador que forrajea la presa. Existen diferentes clases de depredadores en los que caen los organismos y cada clase tiene distintas estrategias de alimentación y depredación.

•    Los verdaderos depredadores atacan a un gran número de presas a lo largo de su vida. Matan a sus presas inmediatamente o poco después del ataque. Pueden comer todo o solo parte de su presa. Los verdaderos depredadores incluyen tigres, leones, ballenas, tiburones, aves que comen semillas, hormigas y humanos.^[10]​
•    Los pastores comen sólo una porción de su presa. Dañan a la presa, pero rara vez la matan. Los pastores incluyen antílopes, vacas y mosquitos.
•    Los parásitos, como los pastores, comen solo una parte de su presa (huésped), pero rara vez todo el organismo. Pasan todo o gran parte de su ciclo de vida viviendo en / en un solo huésped. Esta relación íntima es típica de tenias, pulgas hepáticas y parásitos de plantas, como el mildiu de la patata (Phytophthora infestans).
•    Los parasitoides son principalmente típicos de las avispas parasitoides (orden Hymenoptera), y algunas moscas (orden Diptera). Los huevos se ponen dentro de las larvas de otros artrópodos, eclosionan y consumen al huésped desde el interior, matándolo. Esta inusual relación depredador-huésped es típica de aproximadamente el 10% de todos los insectos. [8] Muchos virus que atacan a los organismos unicelulares (como los bacteriófagos) también son parasitoides; se reproducen dentro de un único huésped que inevitablemente es asesinado por la asociación.

Avispa parasitoide

La optimización de estas diferentes estrategias de alimentación y depredación puede explicarse por la teoría de la alimentación óptima. En cada caso, hay costos, beneficios y limitaciones que determinan en última instancia la regla de decisión óptima que debe seguir el depredador.

El modelo de dieta óptima.

Una versión clásica de la teoría de forrajeo óptimo es el modelo de dieta óptima, que también se conoce como modelo de elección de presa o modelo de contingencia. En este modelo, el depredador se encuentra con diferentes elementos de presas y decide si comer lo que tiene o buscar un elemento de presa más rentable. El modelo predice que los forrajeadores deben ignorar los elementos de presa de baja rentabilidad cuando hay elementos más rentables presentes y abundantes.^[11]​

La rentabilidad de un objeto de presa depende de varias variables ecológicas. E es la cantidad de energía (calorías) que un elemento de presa proporciona al depredador. El tiempo de manejo (h) es la cantidad de tiempo que tarda el depredador en manejar la comida, desde el momento en que el depredador encuentra el elemento de presa hasta el momento en que se come el elemento de presa. La rentabilidad de un objeto de presa se define entonces como E / h. Además, el tiempo de búsqueda (S) es la cantidad de tiempo que tarda el depredador en encontrar un objeto de presa y depende de la abundancia de la comida y la facilidad para localizarla.^[8]​ En este modelo, la moneda es el consumo de energía por unidad de tiempo y las restricciones incluyen los valores reales de E, h y S, así como el hecho de que los elementos de presa se encuentran secuencialmente.

Modelo de elección entre presas grandes y pequeñas.

Koala comiendo

Usando estas variables, el modelo de dieta óptima puede predecir cómo los depredadores eligen entre dos tipos de presas:

• presa grande 1 con valor energético E1 y tiempo de manejo h1, y
• presa pequeña 2 con valor energético E2 y tiempo de manejo h2.

Para maximizar su tasa global de ganancia de energía, un depredador debe considerar la rentabilidad de los dos tipos de presas. Si se supone que la presa grande 1 es más rentable que la presa pequeña 2, entonces E1 / h1> E2 / h2. Por lo tanto, si el depredador se encuentra con la presa 1, siempre debe elegir comerla, debido a su mayor rentabilidad. Nunca debe molestarse en buscar la presa 2. Sin embargo, si el animal se encuentra con la presa 2, debe rechazarla para buscar una presa más rentable 1, a menos que el tiempo que tome encontrar una presa 1 sea demasiado largo y costoso para que valga la pena. Por lo tanto, el animal solo debe comer la presa 2 si E2 / h2> E1 / (h1 + S1), donde S1 es el tiempo de búsqueda de la presa 1. Como siempre es favorable elegir comer la presa 1, la elección de comer la presa 1 no depende de la abundancia de la presa 2. Pero como la longitud de S1 (es decir, lo difícil que es encontrar la presa 1) depende lógicamente de la densidad de la presa 1, la elección de comer la presa 2 depende de la abundancia de la presa 1.^[7]​

Dietas generalistas y especializadas.

El modelo de dieta óptima también predice que diferentes tipos de animales deberían adoptar diferentes dietas basadas en variaciones en el tiempo de búsqueda. Esta idea es una extensión del modelo de elección de presa del apartado anterior. La ecuación, E2 / h2> E1 / (h1 + S1), se puede reorganizar para dar: S1> [(E1h2) / E2] - h1. Esta forma reorganizada proporciona el umbral de cuánto tiempo debe ser S1 para que un animal elija comer la presa 1 o la presa 2.^[7]​ Los animales que tienen S1 que alcanza el umbral se definen como generalistas. En la naturaleza, los generalistas incluyen una amplia gama de elementos de presa en su dieta.^[12]​ Un ejemplo de un generalista es un ratón, que consume una gran variedad de semillas, granos y nueces.^[13]​

En contraste, los depredadores con S1 relativamente cortos están mejor eligiendo solo comer presas 1. Estos tipos de animales se definen como especialistas y tienen dietas muy exclusivas en la naturaleza.^[12]​ Un ejemplo de especialista es el koala, que solo consume hojas de eucalipto.^[14]​ En general, los diferentes animales en las cuatro clases funcionales de depredadores exhiben estrategias que abarcan un continuo entre ser un generalista y un especialista. Además, dado que la elección de comer las presas 2 depende de la abundancia de presas 1 (como se mencionó anteriormente), si la presa 1 llega a ser tan escasa que S1 alcanza el umbral, el animal debería cambiar de comer exclusivamente presas 1 a comer presas 1 y presas 2.^[7]​ En otras palabras, si la comida dentro de la dieta de un especialista se vuelve muy escasa, un especialista a veces puede cambiar a ser un generalista.

Figura 2. Tres tipos de curvas de respuesta funcional. Adaptado de Staddon.

Curvas de respuesta funcional.

Como se mencionó anteriormente, la cantidad de tiempo que lleva buscar un objeto de presa depende de la densidad de la presa. Las curvas de respuesta funcional muestran la tasa de captura de presas en función de la densidad de los alimentos y se pueden usar junto con la teoría de la dieta óptima para predecir el comportamiento de alimentación de los depredadores. Hay tres tipos diferentes de curvas de respuesta funcional.^[15]​

Puercoespines

Para una curva de respuesta funcional Tipo I, la tasa de captura de presas aumenta linealmente con la densidad de los alimentos. A bajas densidades de presas, el tiempo de búsqueda es largo. Dado que el depredador pasa la mayor parte del tiempo buscando, se come cada objeto de presa que encuentra. A medida que aumenta la densidad de presas, el depredador es capaz de capturar la presa cada vez más rápido. En cierto punto, la tasa de captura de presas es tan alta que el depredador no tiene que comerse todos los objetos de presa que encuentra. Después de este punto, el depredador solo debe elegir los objetos de presa con la E / h más alta.^[16]​

Para una curva de respuesta funcional Tipo II, la tasa de captura de presas se acelera negativamente a medida que aumenta con la densidad de los alimentos.^[15]​ Esto se debe a que asume que el depredador está limitado por su capacidad para procesar alimentos. En otras palabras, a medida que aumenta la densidad de los alimentos, aumenta el tiempo de manipulación. Al comienzo de la curva, la tasa de captura de presas aumenta casi linealmente con la densidad de presas y casi no hay tiempo de manejo. A medida que aumenta la densidad de presas, el depredador pasa cada vez menos tiempo buscando presas y más y más tiempo manejando a la presa. La tasa de captura de presas aumenta cada vez menos, hasta que finalmente se estabiliza. El alto número de presas básicamente "invade" al depredador.^[16]​

Una curva de respuesta funcional tipo III es una curva sigmoide. La tasa de captura de presas aumenta al principio con la densidad de presa a una tasa acelerada positivamente, pero luego a densidades altas, la forma se acelera negativamente, similar a la de la curva Tipo II. En densidades de presa altas (la parte superior de la curva), cada nuevo objeto de presa se captura casi de inmediato. El depredador puede ser selectivo y no come todos los elementos que encuentra. Por lo tanto, asumiendo que hay dos tipos de presas con diferentes rendimientos que están en gran abundancia, el depredador elegirá el elemento con la E / h más alta. Sin embargo, a bajas densidades de presas (la parte inferior de la curva) la tasa de captura de presas aumenta más rápido que de forma lineal. Esto significa que a medida que el depredador se alimenta y el tipo de presa con el E / h superior se vuelve menos abundante, el depredador comenzará a cambiar su preferencia al tipo de presa con el E / h inferior, porque ese tipo será relativamente más abundante. Este fenómeno se conoce como cambio de presa.^[15]​

Interacción depredador-presa

La coevolución depredador-presa a menudo hace que sea desfavorable para un depredador el consumo de ciertos objetos de presa, ya que muchas defensas antipredadoras aumentan el tiempo de manejo. [15] Los ejemplos incluyen las plumas de puercoespín, la palatabilidad y la digestibilidad de la rana venenosa, la cripsis y otras conductas de evitación de depredadores. Además, debido a que las toxinas pueden estar presentes en muchos tipos de presas, los depredadores incluyen una gran variabilidad en sus dietas para evitar que cualquier toxina alcance niveles peligrosos. Por lo tanto, es posible que un enfoque que se centre solo en la ingesta de energía no explique completamente el comportamiento de forrajeo de un animal en estas situaciones.

Figura 3. Teorema del valor marginal mostrado gráficamente.

El teorema del valor marginal y el forrajeo óptimo.

El teorema del valor marginal es un tipo de modelo de optimalidad que a menudo se aplica al forrajeo óptimo. Este teorema se usa para describir una situación en la que un organismo que busca alimento en una parcela (o zona) debe decidir cuándo es económicamente favorable salir. Mientras que el animal está dentro de una parcela, experimenta la ley de rendimientos decrecientes, donde cada vez es más difícil encontrar una presa a medida que pasa el tiempo. Esto puede deberse a que la presa se está agotando, la presa comienza a tomar medidas evasivas y se vuelve más difícil de atrapar, o el depredador comienza a cruzar su propio camino más a medida que busca.^[7]​ Esta ley de rendimientos decrecientes se puede mostrar como una curva de ganancia de energía por tiempo empleado en una parcela (Figura 3). La curva comienza con una pendiente pronunciada y se nivela gradualmente a medida que la presa se vuelve más difícil de encontrar. Otro costo importante a considerar es el tiempo de viaje entre diferentes parcelas y el sitio de anidación. Un animal pierde tiempo de alimentación mientras viaja y gasta energía a través de su locomoción.^[8]​

En este modelo, la moneda que se optimiza es generalmente la ganancia de energía neta por unidad de tiempo. Las restricciones son el tiempo de viaje y la forma de la curva de rendimientos decrecientes. Gráficamente, la moneda (ganancia de energía neta por unidad de tiempo) viene dada por la pendiente de una línea diagonal que comienza al comienzo del tiempo de viaje y se interseca con la curva de rendimientos decrecientes (Figura 3). Para maximizar la moneda, uno quiere la línea con la mayor pendiente que aún toca la curva (la línea tangente). El lugar donde esta línea toca la curva proporciona la regla de decisión óptima de la cantidad de tiempo que el animal debe pasar en una parcela antes de irse.

Figura 4. Curva de rentabilidad de la captura del mejillón por los ostreros. Adaptado de Meire y Ervynck..^[17]​

Ostrero. Dan Pancamo

Ejemplos de modelos de forrajeo óptimo en animales.

Forrajeo óptimo de los ostreros

La alimentación de mejillones de los ostreros proporciona un ejemplo de cómo se puede utilizar el modelo de dieta óptima. Los ostreros se alimentan de mejillones y los abren por su cuenta. Las limitaciones para estas aves son las características de los diferentes tamaños de mejillón. Mientras que los mejillones grandes proporcionan más energía que los mejillones pequeños, los mejillones grandes son más difíciles de abrir debido a sus conchas más gruesas. Esto significa que mientras los mejillones grandes tienen un mayor contenido de energía (E), también tienen un tiempo de abertura más largo (h). La rentabilidad de cualquier mejillón se calcula como E / h. Los ostreros deben decidir qué tamaño de mejillón proporcionará suficiente nutrición para superar el costo y la energía requerida para abrirlo.^[8]​

Estornino europeo

En su estudio, Meire y Ervynck intentaron modelar esta decisión al grafiar las ganancias relativas de los mejillones de diferentes tamaños. Crearon una curva en forma de campana, lo que indicaba que los mejillones de tamaño moderado eran los más rentables. Sin embargo, observaron que si un ostrero rechazaba demasiados pequeños mejillones, el tiempo necesario para buscar el próximo mejillón adecuado aumentaba considerablemente. Esta observación cambió su curva de campana hacia la derecha (Figura 4). Sin embargo, aunque este modelo predijo que los ostreros preferirían los mejillones de 50–55 mm, los datos observados mostraron que los ostreros en realidad prefieren los mejillones de 30–45 mm. Meire y Ervynk se dieron cuenta de que la preferencia por el tamaño del mejillón no solo dependía de la rentabilidad de la presa, sino también de la densidad de la presa. Después de que esto fue contabilizado, encontraron un buen acuerdo entre la predicción del modelo y los datos observados.^[18]​

Forrajeo óptimo en los estorninos.

Figura 5. Si los estorninos están maximizando la tasa neta de ganancia de energía, un tiempo de viaje más largo resulta en una carga óptima más grande. Adaptado de Krebs y Davies.

Abeja en su colmena

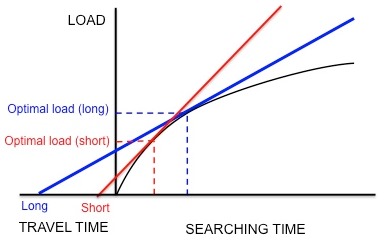
El comportamiento de alimentación del estornino europeo, sturnus vulgaris, proporciona un ejemplo de cómo se usa el teorema del valor marginal para modelar la alimentación óptima. Los estorninos dejan sus nidos y viajan a áreas de comida en busca de larvas para llevar a sus crías. Los estorninos deben determinar el número óptimo de elementos de presa para trasportar en un viaje (es decir, el tamaño de carga óptimo). Mientras que los estorninos se alimentan dentro de un área, experimentan rendimientos decrecientes: el estornino solo puede mantener algunas larvas en su buche, por lo que la velocidad con la que el padre recoge las larvas disminuye con la cantidad de larvas que ya tiene en su buche . Por lo tanto, las restricciones son la forma de la curva de los rendimientos decrecientes y el tiempo de viaje (el tiempo que toma hacer un viaje desde el nido a un área y viceversa). Además, se supone que la moneda es la ganancia de energía neta por unidad de tiempo.^[7]​ Usando esta moneda y las restricciones, se puede predecir la carga óptima dibujando una línea tangente a la curva de rendimientos decrecientes, como se explicó anteriormente (Figura 3).

Bluegill (Lepomis macrochirus)

Kacelnik et al. quería determinar si esta especie efectivamente optimiza la ganancia de energía neta por unidad de tiempo, según la hipótesis.^[19]​ Diseñaron un experimento en el que los estorninos fueron entrenados para recolectar gusanos de la harina de un alimentador artificial a diferentes distancias del nido. Los investigadores generaron artificialmente una curva fija de rendimientos decrecientes para las aves al dejar caer gusanos de la harina a intervalos sucesivamente más y más largos. Las aves continuaron recolectando gusanos de la harina a medida que se presentaban, hasta que alcanzaron una carga "óptima" y volaron a casa. Como muestra la Figura 5, si los estorninos estuvieran maximizando la ganancia de energía neta por unidad de tiempo, un tiempo de viaje corto predeciría una carga óptima pequeña y un tiempo de viaje largo predeciría una carga óptima mayor. De acuerdo con estas predicciones, Kacelnik descubrió que cuanto mayor es la distancia entre el nido y el alimentador artificial, mayor es el tamaño de la carga. Además, los tamaños de carga observados se correspondían cuantitativamente con las predicciones del modelo. Otros modelos basados en diferentes monedas, como la energía ganada por energía gastada (es decir, eficiencia energética), no pudieron predecir los tamaños de carga observados con la mayor precisión. Por lo tanto, Kacelnik concluyó que los estorninos maximizan la ganancia de energía neta por unidad de tiempo. Esta conclusión no fue refutada en experimentos posteriores.^[20]​^[21]​

Forrajeo óptimo en abejas

Las abejas obreras proporcionan otro ejemplo del uso del teorema del valor marginal para modelar el comportamiento óptimo de forrajeo. Las abejas se alimentan de flor en flor recogiendo el néctar para llevar de vuelta a la colmena. Si bien esta situación es similar a la de los estorninos, tanto las restricciones como la moneda son realmente diferentes para las abejas.

Una abeja no experimenta rendimientos decrecientes debido al agotamiento del néctar o cualquier otra característica de las flores en sí. La cantidad total de néctar forrajado aumenta linealmente con el tiempo empleado en una zona. Sin embargo, el peso del néctar agrega un costo significativo al vuelo de la abeja entre las flores y su viaje de regreso a la colmena. Wolf y Schmid-Hempel demostraron, al colocar experimentalmente diferentes pesos en la espalda de las abejas, que el costo del néctar pesado es tan grande que acorta la vida útil de las abejas.^[22]​ Cuanto más corta es la vida útil de una abeja obrera, menos tiempo total tiene para contribuir a su colonia. Por lo tanto, hay una curva de rendimientos decrecientes para el rendimiento neto de energía que recibe la colmena a medida que la abeja recolecta más néctar durante un viaje.^[7]​

Crappie blanco

El costo del néctar pesado también afecta la moneda utilizada por las abejas. A diferencia de los estorninos en el ejemplo anterior, las abejas maximizan la eficiencia energética (energía ganada por energía gastada) en lugar de la tasa neta de ganancia de energía (energía neta ganada por tiempo). Esto se debe a que la carga óptima predicha al maximizar la tasa neta de ganancia de energía es demasiado pesada para las abejas y acorta su vida útil, disminuyendo su productividad general para la colmena, como se explicó anteriormente. Al maximizar la eficiencia energética, las abejas pueden evitar gastar demasiada energía en cada viaje y pueden vivir el tiempo suficiente para maximizar su productividad de por vida para su colmena.^[7]​ En un artículo diferente, Schmid-Hempel mostró que la relación observada entre el tamaño de la carga y el tiempo de vuelo está bien correlacionada con las predicciones basadas en maximizar la eficiencia energética, pero muy mal correlacionada con las predicciones basadas en maximizar la tasa neta de ganancia de energía.^[23]​

Forrajeo óptimo en peces centrárquidos

La naturaleza de la selección de presas por dos centrárquidos (crappie blanco y pez bluegill) se ha presentado como un modelo que incorpora estrategias de forrajeo óptimas por Manatunge y Asaeda.^[24]​ El campo visual del pez representado por la distancia reactiva se analizó en detalle para estimar el número de encuentros de presas por búsqueda. Las distancias reactivas predichas fueron comparadas con datos experimentales. El costo energético asociado con el comportamiento de forrajeo de los peces se calculó en función de la secuencia de eventos que tiene lugar para cada presa consumida. Las comparaciones de la abundancia relativa de especies de presas y categorías de tamaño en el estómago al entorno del lago indicaron que tanto el tipo de pez blanco como el agallas azules (longitud <100 mm) seleccionan a las presas utilizando una estrategia de optimización de energía. En la mayoría de los casos, los peces seleccionaron exclusivamente grandes Daphnia ignorando tipos de presas evasivas (Cyclops, Diaptomids) y cladocera pequeña. Esta selectividad es el resultado de que los peces evitan activamente las presas con altas capacidades de evasión, aunque parecen tener un alto contenido energético y se han traducido en selectividad óptima a través de las tasas de éxito de captura. La consideración energética y el sistema visual, aparte de la capacidad del forrajero para capturar presas, son los principales determinantes de la selectividad de presas para el pez luna azul de gran tamaño y el crappie blanco que aún se encuentran en las etapas planctívoras.

Crítica y limitaciones de la teoría del forrajeo óptimo.

Aunque muchos estudios, como los que se citan en los ejemplos anteriores, brindan apoyo cuantitativo para la teoría de forrajeo óptimo y demuestran su utilidad, el modelo ha recibido críticas con respecto a su validez y limitaciones.

Primero, la teoría de forrajeo óptimo se basa en el supuesto de que la selección natural optimizará las estrategias de forrajeo de los organismos. Sin embargo, la selección natural no es una fuerza todopoderosa que produce diseños perfectos, sino más bien un proceso pasivo de selección para rasgos genéticos que aumentan el éxito reproductivo de los organismos. Dado que la genética implica interacciones entre loci, recombinación y otras complejidades, no hay garantía de que la selección natural pueda optimizar un parámetro de comportamiento específico.^[25]​

Además, la TFO también supone que los comportamientos de forrajeo pueden ser moldeados libremente por la selección natural, porque estos comportamientos son independientes de otras actividades del organismo. Sin embargo, dado que los organismos son sistemas integrados, en lugar de agregados mecánicos de partes, este no es siempre el caso. Por ejemplo, la necesidad de evitar a los depredadores puede obligar a los forrajeros a alimentarse menos que la tasa óptima. Por lo tanto, los comportamientos de forrajeo de un organismo pueden no estar optimizados como lo predeciría la TFO, porque no son independientes de otros comportamientos.^[26]​

Otra limitación de la TFO es que carece de precisión en la práctica. En teoría, un modelo de forrajeo óptimo brinda a los investigadores predicciones cuantitativas específicas sobre la regla de decisión óptima de un depredador en función de las hipótesis sobre la moneda y las restricciones del sistema. Sin embargo, en realidad, es difícil definir conceptos básicos como el tipo de presa, las tasas de encuentro o incluso una zona según lo percibe el forrajero.^[25]​ Por lo tanto, si bien las variables de la TFO pueden parecer consistentes teóricamente, en la práctica, pueden ser arbitrarias y difíciles de medir.

Además, aunque la premisa de la TFO es maximizar la aptitud física de un organismo, muchos estudios solo muestran correlaciones entre el comportamiento de alimentación observado y previsto y no llegan a probar si la conducta del animal en realidad aumenta su aptitud reproductiva. Es posible que en ciertos casos, no haya ninguna correlación entre los rendimientos de forrajeo y el éxito reproductivo en absoluto.^[25]​ Sin tener en cuenta esta posibilidad, muchos estudios que utilizan la TFO permanecen incompletos y no abordan ni prueban el punto principal de la teoría.

Una de las críticas más imperativas de la TFO es que puede no ser realmente comprobable. Este problema surge siempre que hay una discrepancia entre las predicciones del modelo y las observaciones reales. Es difícil decir si el modelo es fundamentalmente incorrecto o si una variable específica se ha identificado incorrectamente o se ha omitido. Debido a que es posible agregar infinitas modificaciones plausibles al modelo, el modelo de optimalidad nunca puede ser rechazado.^[25]​ Esto crea el problema de que los investigadores configuren su modelo para que se ajuste a sus observaciones, en lugar de probar rigurosamente sus hipótesis sobre el comportamiento de alimentación del animal.

Referencias

1. Gutierrez, G. Estrategias de forrajeo
2. Monge-Nájera, J. (2019). «¿Cómo se traduce “foraging” al español?». Blog RBT. Consultado el 6 de febrero de 2020. 
3. Parker, G. A.; Smith, J. M. (1990). «Optimality theory in evolutionary biology». Nature 348 (6296): 27. Bibcode:1990Natur.348...27P. doi:10.1038/348027a0. 
4. Werner, E. E.; Hall, D. J. (1974). «Optimal Foraging and the Size Selection of Prey by the Bluegill Sunfish (Lepomis macrochirus)». Ecology 55 (5): 1042. doi:10.2307/1940354. 
5. Sinervo, Barry (1997). "Optimal Foraging Theory: Constraints and Cognitive Processes" Archivado el 23 de noviembre de 2015 en Wayback Machine., pp. 105–130 in Behavioral Ecology. University of California, Santa Cruz.
6. 1955-, Stephens, David W., (1986). Foraging theory. Princeton University Press. ISBN 0691084416. OCLC 13902831. Consultado el 17 de octubre de 2018. 
7. Wyers, E. J. (1989). «Behavioral ecology: Adaptational models and behavior. A review ofAn Introduction to Behavioural Ecology (Second Edition), by J.R. Krebs and N.B. Davies, Oxford, Blackwell Scientific, 1987, 389 pp., $22.95, cloth». Zoo Biology 8 (3): 307-309. ISSN 0733-3188. doi:10.1002/zoo.1430080312. Consultado el 17 de octubre de 2018. 
8. CALIFORNIA UNIV SANTA CRUZ (10 de marzo de 1993). Final Report for Contract N00014-91-J-1815 (University of California, Santa Cruz). Defense Technical Information Center. Consultado el 17 de octubre de 2018. 
9. Verlinden, Chris; Wiley, R. Haven (1989-07). «The constraints of digestive rate: An alternative model of diet selection». Evolutionary Ecology (en inglés) 3 (3): 264-272. ISSN 0269-7653. doi:10.1007/bf02270727. Consultado el 17 de octubre de 2018. 
10. Cortés, Enric; Gruber, Samuel H. (1990). «Diet, Feeding Habits and Estimates of Daily Ration of Young Lemon Sharks, Negaprion brevirostris (Poey)». Copeia 1990 (1): 204-218. doi:10.2307/1445836. Consultado el 17 de octubre de 2018. 
11. Giraldeau, Luc-Alain (2009-02). «Foraging Isn't Depleted:Foraging: Behavior and Ecology. David W. Stephens , Joel S. Brown , and Ronald C. Ydenberg , eds. University of Chicago Press, Chicago, 2007. 576 pp., illus. $99.00 (ISBN 9780226772639 cloth).». BioScience 59 (2): 183-184. ISSN 0006-3568. doi:10.1525/bio.2009.59.2.12. Consultado el 17 de octubre de 2018. 
12. Pulliam, H. Ronald (1974-01). «On the Theory of Optimal Diets». The American Naturalist (en inglés) 108 (959): 59-74. ISSN 0003-0147. doi:10.1086/282885. Consultado el 17 de octubre de 2018. 
13. Adler, Gregory H.; Wilson, Mark L. (1987-12). «Demography of a Habitat Generalist, The White-Footed Mouse, in a Heterogeneous Environment». Ecology (en inglés) 68 (6): 1785-1796. ISSN 0012-9658. doi:10.2307/1939870. Consultado el 17 de octubre de 2018. 
14. Shipley, L. A.; Forbey, J. S.; Moore, B. D. (23 de junio de 2009). «Revisiting the dietary niche: When is a mammalian herbivore a specialist?». Integrative and Comparative Biology (en inglés) 49 (3): 274-290. ISSN 1540-7063. doi:10.1093/icb/icp051. Consultado el 17 de octubre de 2018. 
15. Staddon, J. E. R. Adaptive Behavior and Learning. Cambridge University Press. pp. 287-312. ISBN 9781139998369. Consultado el 17 de octubre de 2018. 
16. Jeschke, Jonathan M.; Kopp, Michael; Tollrian, Ralph (2002-02). «PREDATOR FUNCTIONAL RESPONSES: DISCRIMINATING BETWEEN HANDLING AND DIGESTING PREY». Ecological Monographs (en inglés) 72 (1): 95-112. ISSN 0012-9615. doi:10.1890/0012-9615(2002)072[0095:pfrdbh]2.0.co;2. Consultado el 17 de octubre de 2018. 
17. Meire, P. M.; Ervynck, A. (1986). «Are oystercatchers (Haematopus ostralegus) selecting the most profitable mussels (Mytilus edulis)?». Animal Behaviour 34 (5): 1427. doi:10.1016/S0003-3472(86)80213-5. 
18. «Are oystercatchers (Haematopus ostralegus) selecting the most profitable mussels (Mytilus edulis)?». Animal Behaviour (en inglés) 34 (5): 1427-1435. 1 de octubre de 1986. ISSN 0003-3472. doi:10.1016/S0003-3472(86)80213-5. Consultado el 17 de octubre de 2018. 
19. Kacelnik, Alejandro (1984). «Central Place Foraging in Starlings (Sturnus vulgaris). I. Patch Residence Time». Journal of Animal Ecology 53 (1): 283-299. doi:10.2307/4357. Consultado el 17 de octubre de 2018. 
20. Bautista, Luis M.; Tinbergen, Joost; Wiersma, Popko; Kacelnik, Alex (1998-10). «Optimal Foraging and Beyond: How Starlings Cope with Changes in Food Availability». The American Naturalist (en inglés) 152 (4): 543-561. ISSN 0003-0147. doi:10.1086/286189. Consultado el 17 de octubre de 2018. 
21. Bautista, Luis M.; Tinbergen, Joost; Kacelnik, Alejandro (30 de enero de 2001). «To walk or to fly? How birds choose among foraging modes». Proceedings of the National Academy of Sciences (en inglés) 98 (3): 1089-1094. ISSN 0027-8424. PMID 11158599. doi:10.1073/pnas.98.3.1089. Consultado el 17 de octubre de 2018. 
22. Wolf, Thomas J.; Schmid-Hempel, Paul (1989). «Extra Loads and Foraging Life Span in Honeybee Workers». Journal of Animal Ecology 58 (3): 943-954. doi:10.2307/5134. Consultado el 17 de octubre de 2018. 
23. Schmid-Hempel, Paul; Kacelnik, Alejandro; Houston, Alasdair I. (1985-05). «Honeybees maximize efficiency by not filling their crop». Behavioral Ecology and Sociobiology (en inglés) 17 (1): 61-66. ISSN 0340-5443. doi:10.1007/bf00299430. Consultado el 17 de octubre de 2018. 
24. Manatunge, Jagath; Asaeda, Takashi (1998). «Optimal foraging as the criteria of prey selection by two centrarchid fishes». Hydrobiologia (en inglés) 391 (1/3): 221-238. ISSN 0018-8158. doi:10.1023/a:1003519402917. Consultado el 17 de octubre de 2018. 
25. Gray, Russell D. (1987). Foraging Behavior. Springer US. pp. 69-140. ISBN 9781461290278. Consultado el 17 de octubre de 2018. 
26. Pierce, G. J.; Ollason, J. G. (1987). «Eight Reasons Why Optimal Foraging Theory Is a Complete Waste of Time». Oikos 49 (1): 111-118. doi:10.2307/3565560. Consultado el 17 de octubre de 2018. 

Lecturas adicionales

• Bautista, Luis M. y Fernández-Juricic, Esteban. «Optimización del Comportamiento». 2016. Capítulo del libro ´Etología Adaptativa: el comportamiento como producto de la selección natural´. J. Carranza (ed.). pp. 155-193. UCOpress y Publicaciones de la Universidad de Extremadura. Córdoba, España.
• Bautista, Luis M. «Estrategias de alimentación: ¿es posible reducir el comportamiento a tiempo y energía?». 1997. Revista Etologuía, 15:3-8. Sociedad Española de Etología