Tridecágono

Tridecágono
Un tridecágono regular
Características
Tipo	Polígono regular
Lados	13
Vértices	13
Grupo de simetría	${\displaystyle D_{13}}$, orden 2x13
Símbolo de Schläfli	{13} (tridecágono regular)
Diagrama de Coxeter-Dynkin
Polígono dual	Autodual
Área	${\displaystyle A={\frac {13}{4}}a^{2}\cot {\frac {\pi }{13}}}$ (lado ${\displaystyle a}$)
Ángulo interior	≈152.308°
Propiedades
Convexo, isogonal, cíclico
[editar datos en Wikidata]

Tridecágono regular, con sus ángulos principales

En geometría, un tridecágono es un polígono de 13 lados y 13 vértices.

Propiedades

Un tridecágono tiene 65 diagonales, resultado que se puede obtener aplicando la ecuación general para determinar el número de diagonales de un polígono en función del número de lados (${\displaystyle n}$):

${\displaystyle D=n(n-3)/2}$

La suma de todos los ángulos internos de cualquier tridecágono es 1980 grados o ${\displaystyle 11\pi }$ radianes.

Tridecágono regular

Un tridecágono regular es el que tiene todos sus lados de la misma longitud y todos sus ángulos internos iguales. Cada ángulo interno del tridecágono regular mide aproximadamente 152º o exactamente ${\displaystyle 11\pi /13}$ rad. Cada ángulo externo del tridecágono regular mide aproximadamente 27,69º o exactamente ${\displaystyle 2\pi /13}$ rad.

Apotema de tridecagono

La apotema de un tridecágono regular de lado ${\displaystyle L}$ es^[1]​

${\displaystyle a_{p}={\frac {L}{2}}\cdot {\frac {\sin(11\pi /26)}{\sin(\pi /13)}}={\frac {L}{2}}\cdot \cot(\pi /13)\simeq 2,0286\cdot Ledehh4vy}$

siendo ${\displaystyle \cot }$ la función cotangente.

Perímetro

El perímetro de un tridecágono regular es el producto de la longitud de uno de sus lados (${\displaystyle L}$) por trece (número de lados del polígono):

${\displaystyle P=13\cdot L}$

Área

El área de un tridecágono regular es

${\displaystyle A={\frac {P\cdot a_{p}}{2}}={\frac {13\cdot L\cdot a_{p}}{2}}}$

siendo ${\displaystyle P}$ su perímetro, ${\displaystyle L}$ su lado y ${\displaystyle a_{p}}$ su apotema.

El área únicamente en función de su lado ${\displaystyle L}$ es

${\displaystyle A={\frac {13}{4\tan({\frac {\pi }{13}})}}\cdot L^{2}\simeq 13,1858\cdot L^{2}}$

El área únicamente en función de la apotema (${\displaystyle a_{p}}$) del polígono es^[1]​

${\displaystyle A=13\cdot {\frac {\sin(\pi /13)}{\sin(11\pi /26)}}\cdot a_{p}^{2}=13\cdot a_{p}^{2}\cdot \tan(\pi /13)\simeq 3,2042\cdot a_{p}^{2}}$

Construcción

Como 13 es un número primo de Pierpont pero no un número de Fermat, el tridecágono regular no puede ser construido usando regla y compás. Sin embargo, se puede construir utilizando neusis o un dispositivo trisector de ángulos.

La siguiente es una animación de una construcción neusis de un tridecágono regular inscrito en una circunferencia de radio dado ${\displaystyle {\overline {OA}}=12,}$ según Andrew Gleason,^[2]​ basado en trisección del ángulo por medio de un tomahawk (azul claro).

Construcción de un tridecágono regular (triskaidecágono) inscrito en una circunferencia de radio ${\displaystyle \ overline{OA}=12}$ (Animación de 1 min 44 s)
Trisección de un ángulo mediante un tomahawk (azul celeste). Esta construcción se deriva de la siguiente ecuación:
${\displaystyle 12\cos \left({\frac {2\pi }{13}}\right)=2{\sqrt {26-2{\sqrt {13}}}}\cos \left({\frac {1}{3}}\arctan \left({\frac {{\sqrt {3}}\left({\sqrt {13}}+1\right)}{7-{\sqrt {13}}}}\right)\right)+{\sqrt {13}}-1.}$

Aquí se muestra una construcción aproximada de un tridecágono regular usando regla y compás.

Construcción aproximada de un tridecágono

Otra posible animación de una construcción aproximada, también posible con el uso de regla y compás.

Tridecágono, construcción aproximada como animación (3 min 30 s)

Basado en el círculo unitario

• Longitud del lado según la construcción mostrada en GeoGebra, ${\displaystyle a=0.478631328575115\;[unidad\;de\;longitud]}$
• Longitud del lado del tridecágono ${\displaystyle a_{real}=r\cdot 2\cdot \sin \left({\frac {180^{\circ }}{13}}\right)=0.478631328575115\ldots \;[unidad\;de\;longitud]}$
• Error absoluto en la longitud del lado obtenido:

Hasta la precisión máxima de 15 lugares decimales, el error absoluto es de ${\displaystyle F_{a}=a-a_{real}=0.0\;[unidad\;de\;longitud]}$

• Ángulo central construido del tridecágono en GeoGebra (se muestran 13 decimales significativos, redondeados) ${\displaystyle \mu =27.6923076923077^{\circ }}$
• Ángulo central del tridecágono ${\displaystyle \mu _{real}=\left({\frac {360^{\circ }}{13}}\right)=27.{\overline {692307}}^{\circ }}$
• Error angular absoluto del ángulo central construido:

Hasta 13 lugares decimales, el error absoluto es ${\displaystyle F_{\mu }=\mu -\mu _{real}=0.0^{\circ }}$

Ejemplo para ilustrar el error:
En una circunferencia circunscrita de radio r = mil millones de km (una distancia que a la luz le costaría recorrer unos 55 minutos), el error absoluto en la longitud del lado construido sería menor que 1 mm.

Simetría

Simetrías de un tridecágono regular. Los vértices están coloreados según sus posiciones de simetría. Los ejes de simetría se representan en color azul. Los órdenes de las simetrías de giro se anotan en el centro

El "tridecágono regular" posee simetría diedral Dih₁₃ de orden 26. Dado que 13 es un número primo, solo existen un subgrupo con simetría diédrica: Dih₁, y 2 simetrías cíclicas: Z₁₃ y Z₁.

Estas 4 simetrías se pueden ver en las 4 simetrías distintas del tridecágono. John Conway clasificó estas simetrías usando una letra y el orden de la simetría a continuación. Asignó la letra r al grupo de simetría de la figura regular; y para los subgrupos utilizó la letra d (de diagonal) para las figuras con ejes de simetría solo a través de sus vértices; p para figuras con ejes de simetría solo a través de ejes perpendiculares a sus lados; i para figuras con ejes de simetría tanto a través de vértices como a través de centros de lados; y g para aquellas figuras solo con simetría rotacional. Con a1 se etiquetan aquellas figuras con ausencia de simetría. Los tipos de simetrías más bajos permiten disponer de uno o más grados de libertad para definir distintas figuras irregulares.^[3]​ Solo el subgrupo g13 no tiene grados de libertad, pero puede verse como un grafo dirigido. (Véase un ejemplo en la Teoría de grupos de John Conway)

Uso numismático

El tridecágono regular se utiliza como forma en la moneda de 20 coronas checas.^[4]​

Polígonos relacionados

Un tridecagrama es un estrella de 13 lados. Hay 5 formas regulares dadas por los símbolos de Schläfli: {13/2}, {13/3}, {13/4}, {13/5} y {13/6}. Dado que 13 es primo, ninguno de los tridecagramas son figuras compuestas.

Tridecagramas
Imagen	{13/2}	{13/3}	{13/4}	{13/5}	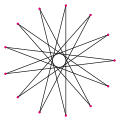{13/6}
Ángulo interno	≈124.615°	≈96.9231°	≈69.2308°	≈41.5385°	≈13.8462°

Polígonos de Petrie

El tridecágono regular es el polígono de Petrie de un símplex:

A12
Símplex

Véase también

• Polígono regular

Referencias

1. Sapiña, R. «Calculadora del área y perímetro del tridecágono regular». Problemas y ecuaciones. ISSN 2659-9899. Consultado el 15 de julio de 2020. 
2. Gleason, Andrew Mattei (March 1988). «Angle trisection, the heptagon, and the triskaidecagon p. 192–194 (p. 193 Fig.4)». The American Mathematical Monthly 95 (3): 186-194. doi:10.2307/2323624. Archivado desde el original el 19 de diciembre de 2015. Consultado el 24 de diciembre de 2015. 
3. John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
4. Colin R. Bruce, II, George Cuhaj, and Thomas Michael, 2007 Standard Catalog of World Coins, Krause Publications, 2006, ISBN 0896894290, p. 81.

Enlaces externos

• Wikimedia Commons alberga una categoría multimedia sobre tridecágonos.
• Weisstein, Eric W. «Tridecagon». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.