Vórtices de Görtler

Vórtices de Görtler en una capa límite

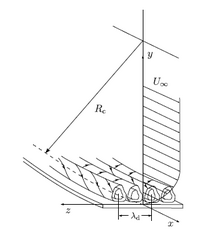
En dinámica de fluidos , los vórtices de Görtler son flujos secundarios que aparecen en un flujo de capa límite a lo largo de una pared cóncava. Si la capa límite es delgada en comparación con el radio de curvatura de la pared, la presión permanece constante a través de la capa límite. Por otro lado, si el grosor de la capa límite es comparable al radio de curvatura, la acción centrífuga crea una variación de presión a través de la capa límite. Esto conduce a la inestabilidad centrífuga, o inestabilidad de Görtler, de la capa límite y la consiguiente formación de «vórtices de Görtler».

Número de Görtler

El inicio de los vórtices de Görtler se puede predecir utilizando el número adimensional denominado número de Görtler ( G ). Es la relación de los efectos centrífugos a los efectos viscosos en la capa límite y se define como:

Simbología

Símbolo	Nombre	Unidad
${\displaystyle \mathrm {G} }$	Número de Görtler
${\displaystyle L}$	Grosor de impulso (Momentum thickness)	m
${\displaystyle R}$	Radio de curvatura de la pared	m
${\displaystyle d}$	Dimensión de área	m
${\displaystyle u}$	Velocidad externa	m / s
${\displaystyle \nu }$	Viscosidad cinemática	m^2 / s

${\displaystyle \mathrm {G} ={\sqrt {\frac {\text{Fuerzas centrífugas}}{\text{Fuerzas viscosas}}}}}$

Deducción

	1	2
Ecuaciones	${\displaystyle \mathrm {G} ={\sqrt {\frac {m\ u^{2}\ /\ R}{\nu \ (\nu \ \rho )}}}}$	${\displaystyle \rho ={\frac {m}{d^{2}\ L}}}$
Simplificando	${\displaystyle \mathrm {G} ={\Bigl (}{\frac {u}{\nu }}{\Bigr )}{\sqrt {\frac {m}{\rho \ R}}}}$
Sustituyendo	${\displaystyle \mathrm {G} ={\Bigl (}{\frac {u}{\nu }}{\Bigr )}{\sqrt {\frac {m}{[m\ /\ (d^{2}\ L)]\ R}}}}$
Simplificando	${\displaystyle \mathrm {G} ={\Bigl (}{\frac {u}{\nu }}{\Bigr )}{\sqrt {\frac {d^{2}\ L}{R}}}}$
Multiplicando ${\displaystyle {\sqrt {\frac {d\ L}{d\ L}}}}$	${\displaystyle \mathrm {G} ={\Bigl (}{\frac {u}{\nu }}{\Bigr )}{\sqrt {{\frac {d^{2}\ L}{R}}{\Bigl (}{\frac {d\ L}{d\ L}}{\Bigr )}}}}$
Simplificando	${\displaystyle \mathrm {G} ={\sqrt {\frac {L}{d}}}{\Bigl (}{\frac {u\ d}{\nu }}{\Bigr )}{\sqrt {\frac {d}{R}}}}$

${\displaystyle \mathrm {G} ={\sqrt {\frac {L}{d}}}{\Bigl (}{\frac {u\ d}{\nu }}{\Bigr )}{\sqrt {\frac {d}{R}}}}$

La inestabilidad de Görtler ocurre cuando G excede alrededor de 0.3.

Otras instancias

Un fenómeno similar que surge de la misma acción centrífuga se observa a veces en los flujos de rotación que no siguen una pared curva, como los vórtices de las costillas observados en las vigas de los cilindros^[1]​ y generados detrás de estructuras móviles.^[2]​

Referencias

1. Williamson, C. H. K. (1996). «Vortex dynamics in the cylinder wake». Annual Review of Fluid Mechanics 28: 477-539. Bibcode:1996AnRFM..28..477W. doi:10.1146/annurev.fl.28.010196.002401. 
2. Buchner, A. J.; Honnery, D.; Soria, J. (2017). «Stability and three-dimensional evolution of a transitional dynamic stall vortex». Journal of Fluid Mechanics 823: 166-197. Bibcode:2017JFM...823..166B. doi:10.1017/jfm.2017.305. Consultado el 2 de noviembre de 2017. 

Bibliografía

• Görtler, H. (1955). «Dreidimensionales zur Stabilitätstheorie laminarer Grenzschichten». Journal of Applied Mathematics and Mechanics 35 (9–10): 362-363. Bibcode:1955ZaMM...35..360.. doi:10.1002/zamm.19550350906. 
• Saric, W. S. (1994). «Görtler vortices». Annu. Rev. Fluid Mech. 26: 379-409. Bibcode:1994AnRFM..26..379S. doi:10.1146/annurev.fl.26.010194.002115.