Árbol (teoría de grafos)
| Árbol | ||
|---|---|---|
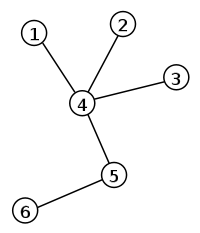 Árbol etiquetado con 6 vértices y 5 aristas. El único camino simple que conecta los vértices 2 y 6 es 2-4-5-6. | ||
| Vértices | v | |
| Aristas | v-1 | |
| Número cromático | 2 si v > 1 | |
| Propiedades | Bipartito, expandible y plano (si el conjunto de vértices es numerable) | |
En teoría de grafos, un árbol es un grafo en el que cualquier par de vértices están conectados por exactamente un camino, o alternativamente, es un grafo conexo acíclico.[1]
Un bosque es un grafo disconexo acíclico. Alternativamente, se puede definir como una unión disjunta de árboles, es decir, es un grafo disconexo cuyas componentes son árboles.[1]
Definiciones
[editar]Un árbol es un grafo simple no dirigido G que satisface cualquiera de estas condiciones alternativas:
- Cualquier par de vértices de G está conectado por exactamente un camino.[1]
- G es conexo y no tiene ciclos.[1]
- G no tiene ciclos y, si se añade alguna arista se forma un ciclo.[1]
- G es conexo y si se le quita alguna arista deja de ser conexo.[1]
- G es conexo y el grafo completo de 3 vértices no es un menor de G.
Las condiciones anteriores son todas equivalentes, es decir, si se cumple una de ellas otras también se cumplen. Para árboles finitos además se cumple que: Si un árbol G tiene un número finito de vértices, n, entonces tiene n − 1 aristas.
Algunas definiciones relacionadas con los árboles son:
- Un grafo unidireccional simple G es un bosque si no tiene ciclos simples.
- Un árbol dirigido es un grafo dirigido que sería un árbol si no se consideraran las direcciones de las aristas. Algunos autores restringen la frase al caso en el que todos las aristas se dirigen a un vértice particular, o todas sus direcciones parten de un vértice particular.
- Un árbol recibe el nombre de árbol con raíz si un vértice ha sido designado raíz. En este caso las aristas tienen una orientación natural hacia o desde la raíz. Los árboles con raíz, a menudo con estructuras adicionales como orden de los vecinos de cada vértice, son una estructura clave en informática; véase árbol (programación).
- Un árbol etiquetado es un árbol en el que cada vértice tiene una única etiqueta. Los vértices de un árbol etiquetado de n vértices reciben normalmente las etiquetas {1,2, ..., n}.
- Un árbol regular u homogéneo es un árbol en el que cada vértice tiene el mismo grado.
- Todo árbol posee una altura. Recorriendo el mismo en forma de grafo dirigido y considerando que las aristas parten desde los vértices hacia algún otro vértice o hacia alguna hoja, de forma tal que todo camino inicia en la raíz y termina en una hoja, puede afirmarse que el árbol posee una altura h. Dicha altura será igual a la longitud del camino con más aristas.
Clasificación
[editar]Un árbol es llamado k-ario si cada nodo tiene, como máximo, k hijos. Un caso particularmente importante es el de un árbol 2-ario, al cual se denomina árbol binario.
Si todos los nodos del árbol exceptuando las hojas, poseen exactamente k hijos, ese árbol además de ser k-ario es completo.
Otro caso particular es el del árbol estrella, el cual consiste de un único nodo, que es la raíz. El resto de sus vértices son hojas. Todo árbol estrella de k vértices tiene un único nodo con k-1 hijos, por lo tanto, todo árbol estrella de k vértices es (k-1)-ario.
Propiedades
[editar]Los árboles son grafos mínimamente conexos, ya que todas sus aristas son puentes o aristas de corte. Por lo tanto, se consideran grafos poco cohesivos.[1]
Un árbol de n vértices tiene n-1 aristas. En general, un bosque de m componentes tiene n-m aristas.[1]
Todo árbol es a su vez un grafo con sólo un conjunto numerable de vértices es además un grafo plano.
Todo grafo conexo G admite un árbol de expansión, que es un árbol que contiene cada vértice de G y cuyas aristas son aristas de G.
Todo árbol k-ario completo de altura h tiene kh hojas.
Dado n vértices etiquetados, hay n n−2 maneras diferentes de conectarlos para construir un grafo. El resultado se llama fórmula de Cayley. El número de árboles con n vértices de grado d1,d2,...,dn es:
que es un coeficiente multinomial.
Contar el número de árboles no etiquetados es un problema complicado. De hecho, no se conoce ninguna fórmula para el número de árboles t(n) con n vértices (debe entenderse aquí el número de árboles diferentes salvo isomorfismo de grafos). Los primeros valores de t(n) son 1, 1, 1, 1, 2, 3, 6, 11, 23, 47, 106, 235, 551, 1301, 3159, ... (sucesión A000055 en OEIS). Otter (1948) probó que
Una fórmula más exacta para el comportamiento asintótico de t(n) implica que hay dos números α y β (α ≈ 3 y β ≈ 0.5) tales que:
Véase también
[editar]Referencias
[editar]Bibliografía
[editar]- Wasserman, Stanley; Faust, Katherine (2013) [1994]. Análisis de redes sociales: Métodos y aplicaciones. Madrid: Centro de Investigaciones Sociológicas. ISBN 978-84-7476-631-8. OCLC 871814053.
Enlaces externos
[editar]- Sobre los grafos VPT y los grafos EPT. Mazzoleni, María Pía. 30 de mayo de 2014.



