Lihtharmooniline võnkumine

Lihtharmooniline võnkumine. Piki püsttelge on suunatud koordinaat x

Siinusfunktsiooni (punane) ja koosinusfunktsiooni (sinine) graafikud: sin (α + 90°) = cos α

Lihtharmooniline võnkumine (inglise keeles simple harmonic motion) on füüsikas süsteemi võnkumine, kus taastav jõud on võrdeline siirdega tasakaaluasendist. Taastav jõud mõjub siirdega vastassuunaliselt. Süsteemi, mille liikumist saab kirjeldada lihtharmoonilise võnkumisena, on nimetatud ka sumbuvuseta vabavõnkumiseks ja sellist võnkumist järgivat objekti lihtharmooniliseks ostsillaatoriks (ingl simple harmonic oscillator).

Lihtharmooniline võnkumine on lihtsaim mitmesuguste võnkumiste (ja seeläbi võnkumiste levimise ruumis ehk lainelevi) kirjeldamise aluseks olev matemaatiline mudel. Lihtharmoonilise võnkumise klassikaliseks näide on vedru küljes oleva massi liikumine juhul kui vedru poolt tekitatava taastava jõu suurus allub Hooke'i seadusele ja sumbuvust ei arvestata. Teine tuntud näide lihtharmoonilisest võnkumisest on sumbuvuseta matemaatilise pendli võnkumine.

Lihtharmooniline võnkumise korral toimub liikumine ajas sinusoidaalselt ehk on kirjeldatav siinus- või koosinusfunktsiooniga. Sel juhul on võnkuva suuruse ${\displaystyle x}$ muutus ajas ${\displaystyle t}$ kirja pandav valemiga

${\displaystyle x(t)=A\cos \,(\omega t+\varphi _{0})}$,

kus ${\displaystyle A}$ on amplituud, ${\displaystyle \omega }$ on ringsagedus ja ${\displaystyle \varphi _{0}}$ võnkumise algfaas. Ringsageduse ${\displaystyle \omega }$ asemel kasutatakse sageli ka sagedust ${\displaystyle f}$, kusjuures ${\displaystyle \omega =2\pi f}$. Võnkumise periood on ${\displaystyle T=1/f}$.

Matemaatiline käsitlus

Definitsioon

Lihtharmooniline on võnkumine, milles taastav jõud on võrdeline (${\displaystyle \propto }$) siirdega tasakaaluasendist. Matemaatiliselt võib lihtharmoonilise võnkumise definitsiooni seega kirja panna järgmiselt:

${\displaystyle {F}\propto {-x},}$

kus ${\displaystyle F}$ tähistab taastavat jõudu ja ${\displaystyle x}$ on siiret tasakaaluasendist (miinusmärgiga rõhutatakse tõsiasja, et tegu on taastava jõuga). Jõud on teatavasti defineeritud, kui massi ja kiirenduse korrutis ${\displaystyle F=ma\Rightarrow F=m{\ddot {x}}}$, seega võib definitsiooni kirjutada kujul

${\displaystyle m{\ddot {x}}\propto -x\Rightarrow {\ddot {x}}\propto -x}$,

ehk definitsiooni võib kirja panna ka järgmiselt: lihtharmooniline on iga võnkumine, milles siire ja kiirendus on võrdelised ja võrdvastupidise suunaga.

Dünaamika

Vastavalt definitsioonile kirjeldab ühedimensioonilist lihtharmoonilist võnkumist konstantsete kordajatega teist järku harilik lineaarne diferentsiaalvõrrand. Kui võtta aluseks massi võnkumise lineaarse vedru küljes, siis vastavalt Hooke'i seadusele on taastavaks jõuks ${\displaystyle F=-kx}$ ja võrdelisuse saab kirjutada võrdusena

${\displaystyle m{\ddot {x}}=-kx}$

kus ${\displaystyle m}$ on võnkuva keha mass, ${\displaystyle x}$ on siire tasakaaluasendist ja ${\displaystyle k}$ on vedru jäikus. Jagades mõlemat poolt massiga ${\displaystyle m}$ ja kasutades tuletise teist kirjaviisi (${\displaystyle {\ddot {x}}}$ teine kirjaviis on ${\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}}$) saame:

${\displaystyle {\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=-{\frac {k}{m}}x;}$

selle diferentsiaalvõrrandi lahendiks on sinusoidaalne funktsioon kujul

${\displaystyle x(t)=c_{1}\cos \left(\omega t\right)+c_{2}\sin \left(\omega t\right),}$

kus konstandid ${\displaystyle {c_{1}}}$ ja ${\displaystyle {c_{2}}}$ määravad algtingimused, nagu algsiire ${\displaystyle c_{1}=x_{1}}$ ja algkiirus ${\displaystyle c_{2}=v_{1}/\omega }$.

Lahendit saab avaldada ka kujul:

${\displaystyle x(t)=A\cos \left(\omega t-\varphi \right),}$

kus

${\displaystyle \omega ={\sqrt {\frac {k}{m}}},\qquad A={\sqrt {{c_{1}}^{2}+{c_{2}}^{2}}},\qquad \tan \varphi ={\frac {c_{2}}{c_{1}}}.}$

Antud suurustel on võnkumiste kirjeldamiseks tuntud ja mõõdetav tähendusː ${\displaystyle A}$ on amplituud (maksimaalne siire tasakaaluasendist), ${\displaystyle \omega }$ on ringsagedus (ehk võngete arv 2π sekundi jooksul) ja ${\displaystyle \varphi }$ võnkumise algfaas (seotud siirdega ajahetkel ${\displaystyle t=0}$).

Kasutades matemaatilist analüüsist tuntud definitsioone, võime tuletiste abil siirdest leida liikumise kiiruse ja kiirenduse:

${\displaystyle v(t)={\frac {\mathrm {d} x}{\mathrm {d} t}}=-A\omega \sin(\omega t-\varphi ),}$

Seejuures esineb suurim kiirus ${\displaystyle v=\omega A}$ liikumisel läbi tasakaaluasendi. Kiiruse tuletis annab kiirenduse

${\displaystyle a(t)={\frac {\mathrm {d} ^{2}x}{\mathrm {d} t^{2}}}=-A\omega ^{2}\cos(\omega t-\varphi ).}$

Suurim kiirendus ${\displaystyle A\omega ^{2}}$ esineb maksimaalsel kaugusel tasakaaluasendist.

Definitsiooni järgi on lihtharmooniliselt võnkuva massi ${\displaystyle m}$ kiirendus võrdeline tema siirdega:

${\displaystyle a(x)=-\omega ^{2}x,}$

kus ${\displaystyle \omega ^{2}={\frac {k}{m}}}$.

Kuna ${\displaystyle \omega =2\pi f}$, siis

${\displaystyle f={\frac {1}{2\pi }}{\sqrt {\frac {k}{m}}}}$

kuna periood ${\displaystyle T={\frac {1}{f}},}$ siis ${\displaystyle T=2\pi {\sqrt {\frac {m}{k}}}.}$

Antud võrranditest on näha, et lihtharmooniline võnkumine on isokroonne, s.t periood ja sagedus on amplituudist ja algfaasist sõltumatud.

Energia

Asendades ω² suurusega k/m, avaldub süsteemi kineetiline energia K

${\displaystyle K(t)={\tfrac {1}{2}}mv^{2}(t)={\tfrac {1}{2}}m\omega ^{2}A^{2}\sin ^{2}(\omega t-\varphi )={\tfrac {1}{2}}kA^{2}\sin ^{2}(\omega t-\varphi ),}$

ja potentsiaalne energia

${\displaystyle U(t)={\tfrac {1}{2}}kx^{2}(t)={\tfrac {1}{2}}kA^{2}\cos ^{2}(\omega t-\varphi ).}$

Hõõrde või teiste liikumist takistavate jõudude puudumisel on süsteemi kogu mehaaniline energia ajas muutumatu

${\displaystyle E=K+U={\tfrac {1}{2}}kA^{2}.}$

Vedru ja massi süsteemi võnkumine

Näited

Mass vedru otsas

Järgnevalt on kirjeldatud füüsikalisi süsteeme, mis on lihtharmooniliste ostsillaatorite näited. Kui vedru jäikusega k külge on kinnitatud Mass m, siis selle liikumine tasakaaluasendi ümber juhul, kui puudub sumbuvus, on lihtharmooniline võnkumine. Niisuguse süsteemi võnkeperioodi saab leida valemiga

${\displaystyle T=2\pi {\sqrt {\frac {m}{k}}},}$

mis näitab, et võnkeperiood ei sõltu amplituudist ega ka raskuskiirendusest.

Lihtharmooniline võnkumine: ühtlaselt pöörleva punkti projektsioon teljele

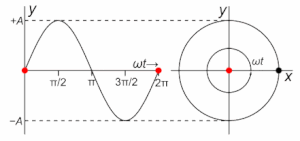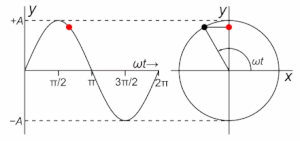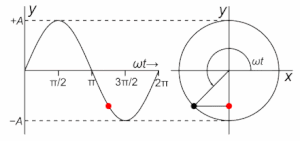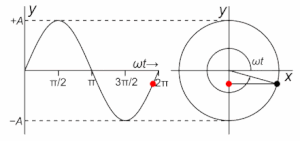
Ühtlane pöörlemine

Lihtharmooniliselt liigub ühtlaselt ringjooneliselt liikuva (nurkkiirenduseta pöörleva) keha punkti projektsioon. Kui keha punkt pöörleb xy-tasandil nurkkiirusega ω pöörlemistsentrist kaugusel r, siis punkti projektsioon liigub koordinaattelgedel lihtharmooniliselt. Seejuures on punkti liikumise amplituud võrdne kaugusega pöörlemistsentrist r ja võnkumise ringsagedus on võrdne pöörlemise nurkkiirusega ω. Igal ajahetkel on punkti projektsioon x-teljele leitav vastavalt:

${\displaystyle x=r\cos(\omega t).}$

Võttes antud seosest esimese ja teise tuletise aja järgi saame:

${\displaystyle {\dot {x}}=-r\omega \sin(\omega t),\quad {\ddot {x}}=-r\omega ^{2}\cos(\omega t),}$

viimase saab ümber kirjutada:

${\displaystyle {\ddot {x}}=-\omega ^{2}x}$

ehk ühtlaselt pöörleva keha punkti projektsiooni liikumine vastab lihtharmoonilise võnkumise definitsioonile. Kiirendus ja siire on võrdelised.

Matemaatilise pendli sumbuvuseta lihtharmooniline võnkumine

Matemaatiline pendel

Matemaatilise pendli sumbuvuseta võnkumisel väikese amplituudiga võib pendli liikumist lugeda lähedaseks lihtharmoonilisele võnkumisele. Matemaatilise pendli võnkumist kirjeldab diferentsiaalvõrrand

${\displaystyle -mgl\sin \theta =I{\ddot {\theta }},}$

kus m on pendli mass, ${\displaystyle g}$ on raskuskiirendus, l on pendli pikkus, ${\displaystyle I}$ on inertsimoment, ${\displaystyle \theta }$ on pendli niidi nurk vertikaalist ja ${\displaystyle {\ddot {\theta }}}$on antud nurga muutuse kiirendus ehk nurkkiirendus. Väikese amplituudiga võnkumiste korral on ka maksimaalne nurk tasakaaluasendist nullilähedase väärtusega. Nullilähedaste nurkade korral kehtib seos sin θ ≈ θ ja diferentsiaalvõrrand saab kuju

${\displaystyle -mgl\theta =I{\ddot {\theta }},}$

mis teeb nurkkiirenduse ${\displaystyle {\ddot {\theta }}}$ võrdeliseks nurga suurusega ${\displaystyle \theta }$ ja seega viimane diferentsiaalvõrrand rahuldab lihtharmoonilise võnkumise definitsiooni.

Diferentsiaalvõrrandi järgi saab määrata matemaatilise pendli võnkeperioodi. Pikkusega l pendli võnkeperiood on arvutatav valemiga

${\displaystyle T=2\pi {\sqrt {\frac {l}{g}}}}$.

Valemist on näha et pendli võnkeperiood ei sõltu võnkeamplituudist ja pendli massist. Võnkeperiood sõltub raskuskiirendusest ${\displaystyle g}$ ja pendli pikkusest, mistõttu sama pikkusega pendli võnkeperiood on näiteks Kuul pikem kui Maal, sest raskuskiirendus on Kuul väiksem. Kuna raskuskiirenduse ${\displaystyle g}$ väärtus on Maa eri paigus erisugune, on sama pikkusega pendli võnkeperiood samuti erinev.

Vaata ka

• Harmooniline võnkumine
• Võnkumine
• Vabavõnkumine
• Matemaatiline pendel