توزیع برنولی پیوسته

Continuous Bernoulli distribution

تابع چگالی احتمال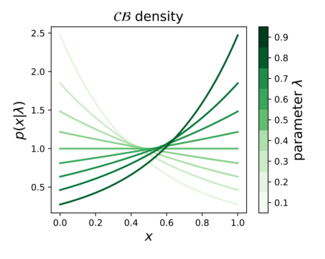
نماد	${\displaystyle {\mathcal {CB}}(\lambda )}$
پارامترها	${\displaystyle \lambda \in (0,1)}$
تکیه‌گاه	${\displaystyle x\in [0,1]}$
تابع چگالی احتمال	${\displaystyle C(\lambda )\lambda ^{x}(1-\lambda )^{1-x}\!}$ where ${\displaystyle C(\lambda )={\begin{cases}2&{\text{if }}\lambda ={\frac {1}{2}}\\{\frac {2\tanh ^{-1}(1-2\lambda )}{1-2\lambda }}&{\text{ otherwise}}\end{cases}}}$
تابع توزیع تجمعی	${\displaystyle {\begin{cases}x&{\text{ if }}\lambda ={\frac {1}{2}}\\{\frac {\lambda ^{x}(1-\lambda )^{1-x}+\lambda -1}{2\lambda -1}}&{\text{ otherwise}}\end{cases}}\!}$
میانگین	${\displaystyle \operatorname {E} [X]={\begin{cases}{\frac {1}{2}}&{\text{ if }}\lambda ={\frac {1}{2}}\\{\frac {\lambda }{2\lambda -1}}+{\frac {1}{2\tanh ^{-1}(1-2\lambda )}}&{\text{ otherwise}}\end{cases}}\!}$
واریانس	${\displaystyle \operatorname {var} [X]={\begin{cases}{\frac {1}{12}}&{\text{ if }}\lambda ={\frac {1}{2}}\\-{\frac {(1-\lambda )\lambda }{(1-2\lambda )^{2}}}+{\frac {1}{(2\tanh ^{-1}(1-2\lambda ))^{2}}}&{\text{ otherwise}}\end{cases}}\!}$

توزیع برنولی پیوسته^[۱][۲][۳] در نظریه احتمالات، آمار و یادگیری ماشین، خانواده‌ای از توزیع‌های احتمال پیوسته‌است که توسط پارامتر ${\displaystyle \lambda \in (0,1)}$ تعریف می‌شود. بازه این توزیع ${\displaystyle [0,1]}$ است و به این شکل تعریف می‌شود:

${\displaystyle p(x|\lambda )\propto \lambda ^{x}(1-\lambda )^{1-x}.}$

توزیع پیوسته برنولی در یادگیری عمیق و بینایی رایانه‌ای، به‌ویژه در زمینه رمزگذارهای خودکار متغیر^[۴][۵] برای مدل‌سازی پیکسل‌های تصاویر طبیعی مورد استفاده قرار می‌گیرد. به این ترتیب، یک همتای احتمالی مناسب برای از دست دادن آنتروپی متقاطع باینری که معمولاً مورد استفاده قرار می‌گیرد، تعریف می‌کند که اغلب برای پیوسته اعمال می‌شود. ${\displaystyle [0,1]}$ داده‌های با ارزش^{[۶][۷][۸][۹]} این عمل به معنای نادیده گرفتن ثابت نرمال کننده توزیع پیوسته برنولی است، زیرا از دست دادن آنتروپی متقاطع باینری تنها یک احتمال لگ واقعی را برای گسسته تعریف می‌کند. ${\displaystyle \{0,1\}}$ داده‌های با ارزش

برنولی پیوسته نیز یک خانواده نمایی از توزیع‌ها را تعریف می‌کند. نوشتن ${\displaystyle \eta =\log \left(\lambda /(1-\lambda )\right)}$ برای پارامتر طبیعی، چگالی را می‌توان به شکل متعارف بازنویسی کرد: ${\displaystyle p(x|\eta )\propto \exp(\eta x)}$ .

توزیع‌های مرتبط

توزیع برنولی

برنولی پیوسته را می‌توان به عنوان نسخه پیوسته توزیع برنولی در نظر گرفت که بر روی مجموعه گسسته ${\displaystyle \{0,1\}}$ و به وسیله تابع چگالی احتمال پایین تعریف می‌شود:

${\displaystyle p(x)=p^{x}(1-p)^{1-x},}$

جایی که ${\displaystyle p}$ یک پارامتر عددی بین ۰ و ۱ است. اعمال همین تابع در بازه پیوسته ${\displaystyle [0,1]}$ منجر به ضریبی از تابع چگالی احتمال پیوسته برنولی می‌شود.

توزیع بتا

توزیع بتا تابع چگالی را پایین را دارد:

${\displaystyle p(x)\propto x^{\alpha -1}(1-x)^{\beta -1},}$

که می‌توان آن را به این شکل نوشت:

${\displaystyle p(x)\propto x_{1}^{\alpha _{1}-1}x_{2}^{\alpha _{2}-1},}$

در اینجا ${\displaystyle \alpha _{1},\alpha _{2}}$ پارامترهای عددی مثبت هستند و ${\displaystyle (x_{1},x_{2})}$ نشان دهنده یک نقطه دلخواه در داخل سادک ${\displaystyle \Delta ^{1}=\{(x_{1},x_{2}):x_{1}>0,x_{2}>0,x_{1}+x_{2}=1\}}$ می‌باشد. با تعویض نقش پارامتر و ورودی در این تابع چگالی، عبارت پایین را به دست می‌آوریم:

${\displaystyle p(x)\propto \alpha _{1}^{x_{1}}\alpha _{2}^{x_{2}}.}$

با اعمال محدودیت ${\displaystyle \alpha _{1}+\alpha _{2}=1}$ و تغییر متغیر ${\displaystyle \lambda =\alpha _{1}}$ به عبارت پایین خواهیم رسید:

${\displaystyle p(x)\propto \lambda ^{x_{1}}(1-\lambda )^{x_{2}},}$

که دقیقاً مطابق با چگالی برنولی پیوسته‌است.

توزیع نمایی

توزیع نمایی محدود به بازه ۰ تا ۱ معادل توزیع برنولی پیوسته با پارامتر مناسب است.

توزیع طبقه ای مستمر

تعمیم چند متغیره برنولی پیوسته، پیوسته-دسته‌ای نامیده می‌شود.^[۱۰]

جستارهای وابسته

• ‌ توزیع بتا
• ‌ توزیع نمایی
• ‌ توزیع برنولی

منابع

1. Loaiza-Ganem, G. , & Cunningham, J. P. (2019). The continuous Bernoulli: fixing a pervasive error in variational autoencoders. In Advances in Neural Information Processing Systems (pp. 13266-13276).
2. PyTorch Distributions. https://pytorch.org/docs/stable/distributions.html#continuousbernoulli
3. Tensorflow Probability. https://www.tensorflow.org/probability/api_docs/python/tfp/edward2/ContinuousBernoulli بایگانی‌شده در ۲۵ نوامبر ۲۰۲۰ توسط Wayback Machine
4. Kingma, D. P. , & Welling, M. (2013). Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114.
5. Kingma, D. P. , & Welling, M. (2014, April). Stochastic gradient VB and the variational auto-encoder. In Second International Conference on Learning Representations, ICLR (Vol. 19).
6. Larsen, A. B. L. , Sønderby, S. K. , Larochelle, H. , & Winther, O. (2016, June). Autoencoding beyond pixels using a learned similarity metric. In International conference on machine learning (pp. 1558-1566).
7. Jiang, Z. , Zheng, Y. , Tan, H. , Tang, B. , & Zhou, H. (2017, August). Variational deep embedding: an unsupervised and generative approach to clustering. In Proceedings of the 26th International Joint Conference on Artificial Intelligence (pp. 1965-1972).
8. PyTorch VAE tutorial: https://github.com/pytorch/examples/tree/master/vae.
9. Keras VAE tutorial: https://blog.keras.io/building-autoencoders-in-keras.html.
10. Gordon-Rodriguez, E. , Loaiza-Ganem, G. , & Cunningham, J. P. (2020). The continuous categorical: a novel simplex-valued exponential family. In 36th International Conference on Machine Learning, ICML 2020. International Machine Learning Society (IMLS).