توزیع هندسی

هندسی

تابع جرم احتمال
تابع توزیع تجمعی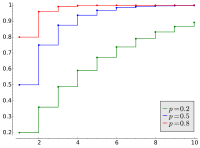
پارامترها	${\displaystyle 0<p\leq 1}$ احتمال پیروزی (حقیقی)	${\displaystyle 0<p\leq 1}$ success probability (real)
تکیه‌گاه	${\displaystyle k\in \{1,2,3,\dots \}\!}$	${\displaystyle k\in \{0,1,2,3,\dots \}\!}$
تابع جرم احتمال	${\displaystyle (1-p)^{k-1}\,p\!}$	${\displaystyle (1-p)^{k}\,p\!}$
تابع توزیع تجمعی	${\displaystyle 1-(1-p)^{k}\!}$	${\displaystyle 1-(1-p)^{k+1}\!}$
میانگین	${\displaystyle {\frac {1}{p}}\!}$	${\displaystyle {\frac {1-p}{p}}\!}$
میانه	${\displaystyle \left\lceil {\frac {-\log(2)}{\log(1-p)}}\right\rceil \!}$ (در صورتی که ${\displaystyle -\log(2)/\log(1-p)}$ عددی طبیعی باشد میانه یکتا نیست.)
مُد	1	0
واریانس	${\displaystyle {\frac {1-p}{p^{2}}}\!}$	${\displaystyle {\frac {1-p}{p^{2}}}\!}$
چولگی	${\displaystyle {\frac {2-p}{\sqrt {1-p}}}\!}$	${\displaystyle {\frac {2-p}{\sqrt {1-p}}}\!}$
کشیدگی	${\displaystyle 6+{\frac {p^{2}}{1-p}}\!}$	${\displaystyle 6+{\frac {p^{2}}{1-p}}\!}$
آنتروپی	${\displaystyle -{\frac {1-p}{p}}\ln(1-p)-\ln p\!}$
تابع مولد گشتاور	${\displaystyle {\frac {pe^{t}}{1-(1-p)e^{t}}}\!}$	${\displaystyle {\frac {p}{1-(1-p)e^{t}}}\!}$
تابع مشخصه	${\displaystyle {\frac {pe^{it}}{1-(1-p)\,e^{it}}}\!}$	${\displaystyle {\frac {p}{1-(1-p)\,e^{it}}}\!}$

توزیع هندسی^[۱] (به انگلیسی: Geometric distribution) توزیعی است گسسته که بیانگر احتمال اولین پیروزی پس از k-1 شکست در فرایند برنولی می‌باشد

${\displaystyle P_{X}(k)={\text{P}}\{X=k\}=(1-p)^{k-1}\,p}$

که در آن p احتمال پیروزی در یک دفعه است.

متغیر تصادفی هندسی

فرض کنید آزمایش‌های مستقلی با احتمال موفقیت p، آن قدر تکرار می‌شود تا یک موفقیت به دست آید. اگر X تعداد آزمایش‌های لازم باشد، آنگاه:

${\displaystyle P\{X=n\}=(1-p)^{n-1}p\qquad n=1,2,3\ldots }$

اثبات

می دانیم شرط لازم و کافی برای X=n آن است که ابتدا، n-1 آزمایش شکست و n اُمین آزمایش موفقیت باشد. از آنجا که برآمدهای متوالی آزمایش‌ها بنا به فرض مستقل هستند داریم ^[۲] :

${\displaystyle p_{X}(k)={\text{P}}\{X=n\}=p(1-p)^{n-1}}$

هر متغیر تصادفی که تابع جرم احتمال به صورت بالا باشد را یک متغیر (فرایند) تصادفی هندسی با پارامتر p می نامیم.

${\displaystyle \sum _{n=1}^{\infty }{\text{Pr}}\{X=n\}=p\sum _{n=1}^{\infty }(1-p)^{n-1}={\frac {p}{1-(1-p)}}=1}$

در نتیجه با احتمال ۱، یک موفقیت بالاخره اتفاق می افتد. هر متغیر تصادفی که تابع جرم احتمال به صورت بالا باشد را یک متغیر تصادفی هندسی با پارامتر p می‌نامیم.

چند مثال ساده

• فرض کنیم می خواهیم رمز عبور 8 کاراکتری یک کامپیوتر را حدس بزنیم. چند مرتبه باید این کار را تکرار کنیم؟
• فرض کنیم یک دارو به احتمال p سبب درمان شود، دارو روی چندمین بیمار مؤثر واقع می‌شود؟
• فرض کنیم احتمال برد یک تیم p باشد، چند مرتبه این تیم باید بازی کند تا یک بازی را ببرد ؟

امید ریاضی متغیر تصادفی هندسی

قصیه: امید ریاضی متغیر تصادفی هندسی با پارامتر p برابر است با

${\displaystyle {\text{E}}[X]={\frac {1}{p}}}$

اثبات

می دانیم ${\displaystyle p_{X}(k)=(1-p)^{k-1}p}$ بنابراین برای محاسبه امید ریاضی می‌بایست عبارت زیر را محاسبه کنیم

${\displaystyle {\text{E}}[X]=\sum _{x}xp_{X}(x)}$

پس با ترکیب دو رابطه ی بالا برای متغیر تصادفی هندسی داریم

${\displaystyle {\text{E}}[X]=\sum _{k=0}^{\infty }k(1-p)^{k-1}p}$

حال اگر فرض کنیم

${\displaystyle F(p)=\sum _{k=0}^{\infty }(1-p)^{k}={\frac {1}{1-(1-p)}}={\frac {1}{p}}}$

داریم

${\displaystyle {\frac {dF(p)}{dp}}=-\sum _{k=0}^{\infty }k(1-p)^{k-1}=-{\frac {1}{p^{2}}}}$

در نتیجه

${\displaystyle {\text{E}}[X]=p{\frac {1}{p^{2}}}={\frac {1}{p}}}$

واریانس متغیر تصادفی هندسی

قضیه: واریانس متغیر تصادفی هندسی با پارامتر p برابر است با

${\displaystyle {\text{var}}[X]={\frac {1-p}{p^{2}}}}$

اثبات

فرض می کنیم پیشامد ${\displaystyle A=\{X=1\}}$ و پیشامد ${\displaystyle B=\{X>1\}}$ با توجه به اینکه A و B افرازهای فضای نمونه ی ما هستند، داریم

${\displaystyle {\text{E}}[X^{2}]={\text{E}}[X^{2}|A]{\text{P}}(A)+{\text{E}}[X^{2}|B]{\text{P}}(B)}$

می‌دانیم

${\displaystyle {\text{E}}[X^{2}|A]={\text{E}}[X^{2}|X=1]=1}$

و

${\displaystyle {\text{E}}[X^{2}|B]={\text{E}}[X^{2}|X>1]={\text{E}}[(X+1)^{2}]={\text{E}}[X^{2}+2X+1]={\text{E}}[X^{2}]+{\frac {2}{p}}+1}$

بنابراین

${\displaystyle {\text{E}}[X^{2}]=1\times p+\left({\text{E}}[X^{2}]+{\frac {2}{p}}+1\right)(1-p)}$

${\displaystyle {\text{E}}[X^{2}]={\frac {2-p}{p^{2}}}}$

در نهایت از آنجا که ${\displaystyle {\text{var}}[X]={\text{E}}[X^{2}]-({\text{E}}[X])^{2}}$ داریم

${\displaystyle {\text{var}}[X]={\frac {2-p}{p^{2}}}-{\frac {1}{p^{2}}}={\frac {1-p}{p^{2}}}}$

متغیر تصادفی هندسی بدون حافظه است !

فرض کنیم می دانیم تعداد دفعاتی که سکه‌ای را اندخته ایم از n بیشتر است، احتمال اینکه سکه را بیش از n+m دفعه بی اندازیم تا شیر بیاید چقدر است ؟

${\displaystyle P(X>n+m|X>n)={\frac {P((X>n+m)\cap (X>n))}{P(X>n)}}={\frac {P(X>n+m)}{P(X>n)}}={\frac {(1-p)^{n+m}}{(1-p)^{n}}}=(1-p)^{m}}$

پس تنها m بار پرتاب بعدی اهمیت دارد و n بار پرتاب اولیه بی‌ارزش می‌شود.

همچنین می‌توان ثابت کرد اگر یک متغیر تصادفی گسسته بی حافظه باشد، هندسی است. (عکس قضیه)

امید ریاضی متغیر تصادفی هندسی

امید ریاضی متغیر تصادفی هندسی با پارامتر p برابر است با:

${\displaystyle E[X]={\frac {1}{p}}}$

اثبات

می‌دانیم:

${\displaystyle P_{X}(k)=(1-p)^{k-1}p}$

و:

${\displaystyle E[X]=\sum _{x}xP_{X}(x)}$

پس با ترکیب دو رابطهٔ بالا برای متغیر تصادفی هندسی داریم:

${\displaystyle E[X]=\sum _{k=0}^{\infty }k(1-p)^{k-1}p}$

حال اگر فرض کنیم:

${\displaystyle F(p)=\sum _{k=0}^{\infty }(1-p)^{k-1}={\frac {1}{1-(1-p)}}={\frac {1}{p}}}$

داریم:

${\displaystyle {\frac {dF(p)}{dp}}=-\sum _{k=0}^{\infty }k(1-p)^{k-1}=-{\frac {1}{p^{2}}}}$

در نتیجه:

${\displaystyle E[X]=p{\frac {1}{p^{2}}}={\frac {1}{p}}}$

واریانس متغیر تصادفی هندسی

واریانس متغیر تصادفی هندسی با پارامتر p برابر است با:

${\displaystyle Var[X]={\frac {1-p}{p^{2}}}}$

اثبات

فرض می‌کنیم پیشامد ${\displaystyle A=\{X=1\}}$ و پیشامد ${\displaystyle B=\{X>1\}}$ :

با توجه به اینکه A و B افرازهای فضای نمونه ی ما هستند، داریم:

${\displaystyle E[X]=E[X|A]P(A)+E[X|B]P(B)}$

${\displaystyle E[X^{2}]=E[X^{2}|A]P(A)+E[X^{2}|B]P(B)}$

در نتیجه:

${\displaystyle E[X^{2}|A]=E[X^{2}|X=1]=1}$

و:

${\displaystyle E[X^{2}|B]=E[X^{2}|X>1]=E[(X+1)^{2}]=E[X^{2}+2X+1]=E[X^{2}]+{\frac {2}{p}}+1}$

پس:

${\displaystyle E[X^{2}]=1*p+(E[X^{2}+{\frac {2}{p}}+1)(1-p)}$

${\displaystyle E[X^{2}]={\frac {2-p}{p^{2}}}}$

در نهایت از آنجا که می‌دانیم ${\displaystyle Var[X]=E[X^{2}]-(E[X])^{2}}$ :

${\displaystyle Var[X]={\frac {2-p}{p^{2}}}-{\frac {1}{p^{2}}}={\frac {1-p}{p^{2}}}}$

منابع

1. «توزیع هندسی» [آمار] هم‌ارزِ «geometric distribution»؛ منبع: گروه واژه‌گزینی. جواد میرشکاری، ویراستار. دفتر یازدهم. فرهنگ واژه‌های مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی. شابک ۹۷۸-۶۰۰-۶۱۴۳-۴۵-۳ (ذیل سرواژهٔ توزیع هندسی)
2. A First Course In Probability 8 Edition-Sheldon Ross

• Wikipedia contributors, "Geometric distribution," Wikipedia, The Free Encyclopedia, http://en.wikipedia.org/w/index.php?title=Geometric_distribution&oldid=340890918 (accessed January 30, 2010).
• Introduction to probabilities models by Sheldon M.Ross
• A First Course In Probability 8Edition-Sheldon Ross
• Athanasios Papoulis-probability and statistics