خوشه‌بندی کی-میانگین

خوشه‌بندی کی-میانگین (به انگلیسی: k-means clustering) روشی در کمی‌سازی بردارهاست که در اصل از پردازش سیگنال گرفته شده و برای آنالیز خوشه‌بندی در داده‌کاوی محبوب است. کی-میانگین خوشه‌بندی با هدف تجزیه ${\displaystyle n}$ مشاهدات به ${\displaystyle k}$ خوشه است که در آن هر یک از مشاهدات متعلق به خوشهای با نزدیکترین میانگین آن است، این میانگین به عنوان پیش‌نمونه استفاده می‌شود. این به پارتیشن‌بندی داده‌های به یک دیاگرام ورونوی تبدیل می‌شود.

تاریخچه الگوریتم

اصطلاح کی-میانگین (به انگلیسی: K-Means Clustering) برای اولین بار توسط جیمز بی مک‌کوین (استاد دانشگاه کالیفرنیا) در سال ۱۹۶۷ مورد استفاده قرار گرفت،^[۱] هرچند این ایده به هوگو استین‌هاوس در سال ۱۹۵۷ باز می‌گردد.^[۲] این الگوریتم ابتدا توسط استوارت لویید در سال ۱۹۵۷ به عنوان یک تکنیک برای مدولاسیون کد پالس پیشنهاد شد و تا سال ۱۹۸۲ خارج از آزمایشگاه‌های بل به انتشار نرسید.^[۳] فورجی در سال ۱۹۶۵ الگوریتمی مشابه را منتشر کرد، به همین دلیل این الگوریتم، الگوریتم لویید-فورجی نیز نامیده می‌شود.^[۴]

توضیحات

با توجه به مجموعه‌ای از مشاهدات ${\displaystyle (x_{1},x_{2},\cdots ,x_{n})}$ که در آن هر یک از مشاهدات یک بردار حقیقی ${\displaystyle d}$-بعدی است. خوشه‌بندی کی-میانگین با هدف پارتیشن‌بندی ${\displaystyle n}$ مشاهدات به ${\displaystyle k\leq n}$ مجموعه ${\displaystyle S=\{S_{1},S_{2},\cdots ,S_{k}\}}$ است به طوری که مجموع مربع اختلاف از میانگین (یعنی واریانس) برای هر خوشه حداقل شود. تعریف دقیق ریاضی آن به این شکل است:

${\displaystyle {\underset {\mathbf {S} }{\operatorname {arg\,min} }}\sum _{i=1}^{k}\sum _{\mathbf {x} \in S_{i}}\left\|\mathbf {x} -{\boldsymbol {\mu }}_{i}\right\|^{2}={\underset {\mathbf {S} }{\operatorname {arg\,min} }}\sum _{i=1}^{k}|S_{i}|\operatorname {Var} (S_{i})}$

که در آن ${\displaystyle \mu _{i}}$ میانگین نقاط در ${\displaystyle S_{i}}$ است. این معادل است با به حداقل رساندن دو به دو مربع انحراف از نقاط در همان خوشه:

${\displaystyle \sum _{{\text{Cluster }}C_{i}}\,\sum _{{\text{Dimension }}d}\,\sum _{x,y\,\in \,C_{i}}(x_{d}-y_{d})^{2}}$

چون کل واریانس ثابت است، از قانون واریانس کلی می‌توان نتیجه گرفت که این معادله برابر است با بیشینه کردن مربع انحرافات بین نقاط خوشه‌های مختلف (BCSS).^[۵]

الگوریتم

الگوریتم استاندارد

رایج‌ترین الگوریتم کی-میانگین با استفاده از یک تکرار شونده پالایش کار می‌کند. این الگوریتم به طور معمول با نام الگوریتم کی-میانگین شناخته می‌شود،‌ اما در میان جامعه علوم کامپیوتر،‌ اغلب آن را با عنوان الگوریتم لوید می‌شناسند.

الگوریتم به این شکل عمل می‌کند:^[۶]

1. ابتدا ${\displaystyle k}$ میانگین یعنی ${\displaystyle \left(\mu _{1}^{(0)},\mu _{2}^{(0)},\cdots ,\mu _{k}^{(0)}\right)}$ را که نماینده خوشه‌ها هستند، به‌صورت تصادفی مقداردهی می‌کنیم.
2. سپس، این دو مرحله پایین را به تناوب چندین بار اجرا می‌کنیم تا میانگین‌ها به یک ثبات کافی برسند و یا مجموع واریانس‌های خوشه‌ها تغییر چندانی نکنند:
   • از میانگین‌ها ${\displaystyle k}$خوشه می‌سازیم، خوشه ${\displaystyle i}$ام در زمان ${\displaystyle t}$ تمام داده‌هایی هستند که از لحاظ اقلیدسی کمترین فاصله را با میانگین ${\displaystyle \mu _{i}^{(t)}}$ یعنی میانگین ${\displaystyle i}$ام در زمان ${\displaystyle t}$ دارند^[۷]. به زبان ریاضی خوشه ${\displaystyle i}$ام در زمان ${\displaystyle t}$ برابر خواهد بود با:
   • ${\displaystyle S_{i}^{(t)}={\big \{}x_{p}:{\big \|}x_{p}-\mu _{i}^{(t)}{\big \|}^{2}\leq {\big \|}x_{p}-\mu _{j}^{(t)}{\big \|}^{2}\ \forall j,1\leq j\leq k{\big \}}}$
3. حال میانگین‌ها را بر اساس این خوشه های جدید به این شکل بروز می‌کنیم:^[۸]
   • ${\displaystyle \mu _{i}^{(t+1)}={\frac {1}{|S_{i}^{(t)}|}}\sum _{x_{j}\in S_{i}^{(t)}}x_{j}}$
4. در نهایت میانگین‌های مرحله آخر (در زمان ${\displaystyle T}$) یعنی ${\displaystyle \left(\mu _{1}^{(T)},\mu _{2}^{(T)},\cdots ,\mu _{k}^{(T)}\right)}$ خوشه‌ها را نمایندگی خواهند کرد.

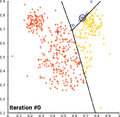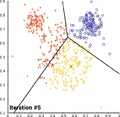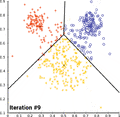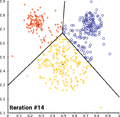
الگوریتم کی-میانگین را می‌توان با پویانمایی پایین برای ${\displaystyle k=3}$ به تصویر کشید.

همگرایی کی-میانگین

کاربردها

خوشه‌بندی کی‌میانگین خوشه‌بندی حتی برای مجموعه داده‌های بزرگ به‌ویژه هنگام استفاده از روش‌های اکتشافی مانند Lloyd's algorithm بسیار آسان است. این با موفقیت در تقسیم‌بندی بازار، بینایی رایانه‌ای و نجوم در میان بسیاری از حوزه‌های دیگر مورد استفاده قرار گرفته است. اغلب به عنوان یک مرحله پیش پردازش برای الگوریتم های دیگر استفاده می شود، به عنوان مثال برای پیدا کردن یک پیکربندی شروع.

کمیت‌سازی برداری

مقالهٔ اصلی: کمیت‌سازی برداری

(تصویر رنگی دو کاناله (برای اهداف تصویری - فقط کانال های قرمز و سبز).

کمی سازی برداری رنگ های موجود در تصویر بالا به سلول های ورونوی با استفاده از خوشه‌بندی کی‌میانگین

خوشه‌بندی کی‌میانگین از پردازش سیگنال سرچشمه می گیرد و هنوز در این حوزه کاربرد دارد. به عنوان مثال، در گرافیک کامپیوتری، رنگ‌سنجی وظیفه کاهش پالت رنگ یک تصویر به تعداد ثابتی k از رنگ‌ها است. الگوریتم کی‌میانگین به راحتی می تواند برای این کار استفاده شود و نتایج قابل رقابتی ایجاد کند. یک مورد استفاده برای این رویکرد بخش‌بندی تصویر است. کاربردهای دیگر کمیت‌سازی برداری عبارتند از نمونه‌گیری غیرتصادفی، زیرا کی‌میانگین به راحتی می‌تواند برای انتخاب k نمونه متفاوت اما مقدماتی از یک مجموعه داده بزرگ برای آنالیزهای بیشتر استفاده شود.

تحلیل خوشه‌ای

مقالهٔ اصلی: خوشه‌بندی

در تحلیل خوشه‌ای می‌توان الگوریتم کی‌میانگین را برای تقسیم‌بندی مجموعه داده ها به k خوشه استفاده کرد. با این حال، الگوریتم کی‌میانگین خالص خیلی منعطف نیست، و به همین دلیل کاربرد محدودی دارد (به جز کمیت‌سازی برداری مانند بالا). به طور خاص، انتخاب پارامتر k سخت است (همانطور که در بالا مورد بحث قرار گرفت) زمانی که توسط قیود خارجی داده نشده باشد. محدودیت دیگر این است که نمی توان آن را با توابع فاصله دلخواه یا روی داده های غیر عددی استفاده کرد. برای این موارد استفاده، بسیاری از الگوریتم های دیگر برتر هستند.

یادگیری ویژگی

خوشه‌بندی کی‌میانگین به عنوان یک مرحله یادگیری ویژگی (یا یادگیری دیکشنری) در (یادگیری نیمه نظارتی یا یادگیری خودران (خودسازمانده) استفاده شده است. ^[۹]

رویکرد اصلی ابتدا آموزش به وسیله الگوریتم خوشه‌بندی کی‌میانگین با استفاده از داده‌های آموزشی ورودی (که نیازی به برچسب گذاری ندارند) است. سپس تصویر کردن هر داده ورودی در فضای ویژگی جدید، و یک تابع «رمزگذاری» مانند مبنای ضرب ماتریس داده‌ها با مکان‌های مرکز داده‌ها، که فاصله هر نمونه را تا مرکز آن محاسبه می کند، یا به سادگی یک تابع نشانگر برای نزدیکترین مرکز،^[۹][۱۰] و یا تبدیل هموار فاصله‌ها. .^[۱۱]

روش دیگر، تبدیل فاصله نمونه-خوشه از طریق یک تابع پایه شعاعی گاوسی می‌باشد که لایه پنهان یک شبکه تابع پایه شعاعی را به دست می‌آورد.^[۱۲] این استفاده از کی‌میانگین به طور موفقیت آمیزی با طبقه‌بندی خطی های ساده برای یادگیری نیمه نظارتی در پردازش زبان طبیعی (NLP) (به ویژه برای دسته‌بندی موجودیت‌های نام‌دار) ترکیب شده است.^[۱۳] در بینایی رایانه‌ای. در یک کار تشخیص شی مشخص شد که عملکرد قابل مقایسه‌ای با رویکردهای یادگیری ویژگی پیچیده‌تری مانند خودرمزگذار و ماشین بولتزمن محدود شده^[۱۱] ارائه می‌دهد. با این حال، معمولاً برای عملکرد معادل به داده‌های بیشتری نیاز دارد، زیرا هر نقطه داده تنها به یک "ویژگی" کمک می‌کند.^[۹]

نگارخانه

• 
  همگرایی کی-میانگین
• 
• 
• 
• 

منابع

1. MacQueen, J. B. (1967). Some Methods for classification and Analysis of Multivariate Observations. Proceedings of 5th Berkeley Symposium on Mathematical Statistics and Probability. Vol. 1. University of California Press. pp. 281–297. MR 0214227. Zbl 0214.46201. Retrieved 2009-04-07.
2. Steinhaus, H. (1957). "Sur la division des corps matériels en parties". Bull. Acad. Polon. Sci. (به فرانسوی). 4 (12): 801–804. MR 0090073. Zbl 0079.16403.
3. Lloyd, S. P. (1957). "Least square quantization in PCM". Bell Telephone Laboratories Paper. Published in journal much later: Lloyd., S. P. (1982). "Least squares quantization in PCM" (PDF). IEEE Transactions on Information Theory. 28 (2): 129–137. doi:10.1109/TIT.1982.1056489. Retrieved 2009-04-15.
4. E.W. Forgy (1965). "Cluster analysis of multivariate data: efficiency versus interpretability of classifications". Biometrics. 21: 768–769. JSTOR 2528559.
5. Kriegel, Hans-Peter; Schubert, Erich; Zimek, Arthur (2016). "The (black) art of runtime evaluation: Are we comparing algorithms or implementations?". Knowledge and Information Systems. 52: 341–378. doi:10.1007/s10115-016-1004-2. ISSN 0219-1377.
6. MacKay, David (2003). "Chapter 20. An Example Inference Task: Clustering" (PDF). Information Theory, Inference and Learning Algorithms. Cambridge University Press. pp. 284–292. ISBN 0-521-64298-1. MR 2012999.
7. Since the square root is a monotone function, this also is the minimum Euclidean distance assignment.
8. Hartigan, J. A.; Wong, M. A. (1979). "Algorithm AS 136: A k-Means Clustering Algorithm". Journal of the Royal Statistical Society, Series C. 28 (1): 100–108. JSTOR 2346830.
9. Coates, Adam; Ng, Andrew Y. (2012). "Learning feature representations with k-means" (PDF). In Montavon, G.; Orr, G. B.; Müller, K.-R. (eds.). Neural Networks: Tricks of the Trade. Springer.
10. Csurka, Gabriella; Dance, Christopher C.; Fan, Lixin; Willamowski, Jutta; Bray, Cédric (2004). Visual categorization with bags of keypoints (PDF). ECCV Workshop on Statistical Learning in Computer Vision.
11. Coates, Adam; Lee, Honglak; Ng, Andrew Y. (2011). An analysis of single-layer networks in unsupervised feature learning (PDF). International Conference on Artificial Intelligence and Statistics (AISTATS). Archived from the original (PDF) on 2013-05-10.
12. Schwenker, Friedhelm; Kestler, Hans A.; Palm, Günther (2001). "Three learning phases for radial-basis-function networks". Neural Networks. 14 (4–5): 439–458. CiteSeerX 10.1.1.109.312. doi:10.1016/s0893-6080(01)00027-2. PMID 11411631.
13. Lin, Dekang; Wu, Xiaoyun (2009). Phrase clustering for discriminative learning (PDF). Annual Meeting of the ACL and IJCNLP. pp. 1030–1038.