اسپیروگراف

اسپیروگراف

پدیدآور	دنیس فیشر
شرکت	هازبرو
کشور	انگلستان
دسترس‌پذیری	۱۹۶۵–امروزه
مواد	پلاستیک
وبگاه رسمی

اسپیروگراف (به انگلیسی: Spirograph) یا اسپیرونگار یا چرخ‌نگار یا زُرفین‌نگار که در ایران با نام دوایر جادوییِ اقلیدس شناخته می‌شود، نوعی اسباب‌بازی است که برای کشیدن اَشکال هندسیِ پدیدآمده از منحنی‌های ریاضی با روشِ درون‌چرخه‌زاد به‌کار می‌رود. اسپیروگراف اولین بار به‌دست دنیس فیشر گسترش یافت و در سال ۱۹۶۵ به بازار ارائه شد.

از واژهٔ اسپیروگراف برای نام بردن از گسترهٔ ابزارهایی که برای کشیدن چنین اشکالی به‌کار می‌روند هم استفاده می‌شود. حتی می‌تواند برای نامیدن منحنی‌های درون‌چرخه‌زاد نیز به‌کار رود. اسپیروگراف از زمان خریده شدنِ شرکت دنیس فیشر به‌دست شرکت اسباب‌بازی‌سازی هازبرو، یک نشان تجاری ثبت‌شدهٔ شرکت هازبرو است.

تاریخچه

طرح‌هایی که با اسپیروگراف (چرخ‌نگار یا دوایر جادوییِ اقلیدس) کشیده شده‌اند.

ابزاری با نام اسپیروگراف ابتدا در سال‌های ۱۸۸۱ تا ۱۹۰۰ به‌دست ریاضیدانی به نام برونو آباکانویچ برای به‌دست‌آوردن مساحت زیر منحنی ساخته شد.^[۱] اسباب‌بازی‌های کشیدنِ اَشکال با چرخ‌دنده حداقل از سال ۱۹۰۸ وجود داشته‌اند؛ در این سال‌ها تبلیغات ابزاری با نام «مارولوس وندرگراف» با کارکردی مشابه در کاتالوگ فروشگاه سیرز چاپ می‌شده‌است.^[۲][۳] مجلهٔ مکانیک پسران در سال ۱۹۱۳ نوشتاری چاپ کرد که چگونگی ساخت ماشینی برای کشیدن وندرگراف را توضیح می‌دهد.^[۴] اما اسپیروگرافِ امروزی به‌دست مهندس انگلیسی، دنیس فیشر، گسترش یافته و اولین بار در سال ۱۹۶۵ در نمایشگاه بین‌المللی اسباب‌بازی نورنبرگ نمایش داده شد. پس از آن، در شرکت خودِ او ساخته شد و امتیاز پخش آن به شرکت اسباب‌بازی کنر داده شد که در سال ۱۹۶۶ فروش آن را در آمریکا با تبلیغ اسباب‌بازی نوآورانهٔ کودکان شروع کرد.

در سال ۱۹۶۸، «کنر» اسباب‌بازی «اسپیروتات» را ساخت که نسخه‌ای ساده‌شده از اسپیروگراف برای کودکانِ پیش از دبستان بود.

کارکرد

اسپیروگراف شامل قطعاتی است که معمولاً آن‌ها را با پلاستیک می‌سازند و به‌صورت دایرهای یا دایره‌های بزرگ توخالی، مثلثی، میلهای و غیره هستند. در اطراف همهٔ آن‌ها دندانههایی وجود دارد که باعث می‌شود در داخل یا محیط دایره‌های بزرگ بتوان آن‌ها را چرخاند. در داخل قطعات معمولاً سوراخ‌هایی وجود دارد که محل قرار گرفتن نوک قلم است و اَشکال مختلف از آن‌ها ایجاد می‌شود.

پایهٔ ریاضی

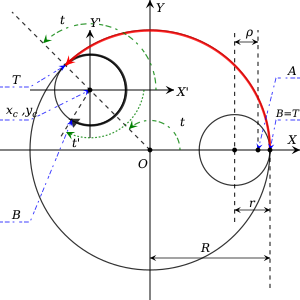
دایرهٔ ثابت ${\displaystyle C_{1}}$ با شعاع ${\displaystyle R}$ را در نظر بگیرید. دایرهٔ کوچک‌تر ${\displaystyle C_{2}}$ با شعاع ${\displaystyle r<R}$ در داخل دایرهٔ اول به‌صورت مماس بر آن می‌گردد. فرض کنید که نقطهٔ ${\displaystyle A}$ در داخل دایرهٔ کوچک‌تر در فاصلهٔ ${\displaystyle \rho <r}$ از مرکز آن قرار گرفته‌باشد. فرض می‌کنیم که نقطهٔ ${\displaystyle A}$ ابتدا بر محور Xها بوده‌است. طرح حاصل از اسپیروگراف از خط سیر نقطهٔ ${\displaystyle A}$ در داخل دایرهٔ بزرگ به‌دست می‌آید.

حال دو نقطه را در نظر بگیرید. نقطهٔ ${\displaystyle T}$ بر دایرهٔ ${\displaystyle C_{1}}$ نقطه‌ای است که دو دایره همیشه با هم در آن در تماس هستند. نقطهٔ ${\displaystyle B}$ بر دایرهٔ ${\displaystyle C_{2}}$ جابجا می‌شود و محل اولیهٔ آن همان نقطهٔ ${\displaystyle T}$ است. با گرداندن ${\displaystyle C_{2}}$ به‌صورت خلاف عقربه‌های ساعت در داخل دایرهٔ ${\displaystyle C_{1}}$، دایرهٔ کوچک‌تر نسبت به مرکزِ خود به‌صورت موافق عقربه‌های ساعت می‌چرخد. فاصله‌ای را که نقطهٔ ${\displaystyle B}$ بر دایرهٔ کوچک‌تر می‌پیماید، با فاصله‌ای که نقطهٔ ${\displaystyle T}$ بر دایرهٔ بزرگ‌تر می‌پیماید برابر است.

پارامترِ ${\displaystyle t}$ را میزان زاویهٔ پیمایش‌شده توسط نقطهٔ مماس و ${\displaystyle {\hat {t}}}$ را میزان چرخش دایرهٔ ${\displaystyle C_{2}}$ در نظر می‌گیریم و ازآنجایی‌که میزان مسافت پیموده‌شده دو دایره برابر است، داریم:

${\displaystyle tR=(t-{\hat {t}})r}$

یا:

${\displaystyle {\hat {t}}=-{\frac {R-r}{r}}t.}$

${\displaystyle (x_{c},y_{c})}$ را مرکز دایرهٔ ${\displaystyle C_{2}}$ در دستگاه مختصات مطلق در نظر گرفته و ${\displaystyle R-r}$ شعاع مماس مرکز دایرهٔ درونی است:

${\displaystyle {\begin{array}{rcl}x_{c}&=&(R-r)\cos t,\\y_{c}&=&(R-r)\sin t.\end{array}}}$

مختصات نقطهٔ ${\displaystyle A}$ در دستگاه مختصات جدید برابرِ ${\displaystyle ({\hat {x}},{\hat {y}})}$ است:

${\displaystyle {\begin{array}{rcl}{\hat {x}}&=&\rho \cos {\hat {t}},\\{\hat {y}}&=&\rho \sin {\hat {t}}.\end{array}}}$

برای به‌دست آوردن مختصات نقطهٔ تماس ${\displaystyle A}$ در دستگاه مختصات قبلی داریم:

${\displaystyle {\begin{array}{rcrcl}x&=&{\hat {x}}+x_{c}&=&(R-r)\cos t+\rho \cos {\hat {t}},\\y&=&{\hat {y}}+y_{c}&=&(R-r)\sin t+\rho \sin {\hat {t}},\\\end{array}}}$

حال، رابطهٔ بین ${\displaystyle t}$ و ${\displaystyle {\hat {t}}}$ را جای‌گذاری می‌کنیم تا مختصات نقطهٔ مماسِ ${\displaystyle A}$ را تنها براساس یک پارامترِ ${\displaystyle t}$ داشته‌باشیم:

${\displaystyle {\begin{array}{rcrcl}x&=&{\hat {x}}+x_{c}&=&(R-r)\cos t+\rho \cos {\frac {R-r}{r}}t,\\[4pt]y&=&{\hat {y}}+y_{c}&=&(R-r)\sin t-\rho \sin {\frac {R-r}{r}}t.\\\end{array}}}$

در نظر می‌گیریم که:

${\displaystyle l={\frac {\rho }{r}}}$ و ${\displaystyle k={\frac {r}{R}}.}$

پارامترِ ${\displaystyle 0\leq l\leq 1}$ نشان‌دهندهٔ میزان دوریِ ${\displaystyle A}$ از مرکز دایرهٔ درونی، و پارامترِ ${\displaystyle 0\leq k\leq 1}$ نشان‌دهندهٔ میزان بزرگیِ دایرهٔ درونی نسبت به دایرهٔ بیرونی است. می‌دانیم که: ${\displaystyle {\frac {\rho }{R}}=lk}$

پس معادلات مماس را چنین به‌دست می‌آوریم:

${\displaystyle {\begin{array}{rcl}x(t)&=&R\left[(1-k)\cos t+lk\cos {\frac {1-k}{k}}t\right],\\[4pt]y(t)&=&R\left[(1-k)\sin t-lk\sin {\frac {1-k}{k}}t\right].\\\end{array}}}$

نگارخانه

• 
  محتویات یکی از بسته‌های دوایر جادوییِ اقلیدس که در ایران به‌فروش می‌رسد.
• 
  چندین طرح که با چرخ‌نگار کشیده شده‌است.
• 
  یک چرخ‌نگار که به‌صورت خط‌کش ساخته شده‌است.
• 
  یک پویانمایی (انیمیشن) از چگونگی کشیدن یک شکل زیبا با چرخ‌نگار.
• 
  یک پویانمایی از چگونگی کشیدن یک شکل با چرخ‌نگار.
• 

جستارهای وابسته

• زیروروکاری
• درون‌چرخه‌زاد

پانویس

1. Goldstein, Cathérine; Gray, Jeremy; Ritter, Jim (1996). L'Europe mathématique: histoires, mythes, identités. Editions MSH. p. 293. Retrieved 17 July 2011.
2. Kaveney, Wendy. "CONTENTdm Collection : Compound Object Viewer". digitallibrary.imcpl.org. Retrieved 17 July 2011.
3. Linderman, Jim. "ArtSlant - Spirograph? No, MAGIC PATTERN!". artslant.com. Archived from the original on 18 June 2010. Retrieved 17 July 2011.
4. "From The Boy Mechanic (1913) - A Wondergraph". marcdatabase.com. 2004 [last update]. Archived from the original on 30 September 2011. Retrieved 17 July 2011. {{cite web}}: Check date values in: |year= (help)

منابع

• مشارکت‌کنندگان ویکی‌پدیا. «Spirograph». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۶ اسفند ۱۳۹۱.

پیوند به بیرون

• یک نرم‌افزار اسپیروگراف برای ویندوز بایگانی‌شده در ۳ مارس ۲۰۱۳ توسط Wayback Machine