روش بارهای تصویر

روش بارهای تصویری (روش تصاویریا روش بارهای آینه ای) یک ابزار پایه در حل مسایل الکتروستاتیک است.این نام برای این روش از آنجا سرچشمه می‌گیرد که ما در این روش عناصر خاصی را در ساختار اولیه مسئله، با بارهای تصویری که همان شرایط مرزی را تکرار می‌کنند، جایگزین می‌کنیم.

قضیه یکتایی

قضیه یکتایی بیان می‌کند که پاسخی از معادله لاپلاس که در شرایط مرزی صدق می‌کند، تنها پاسخی از این نوع است که وجود دارد.واین پاسخ به‌طور یکتا با شرایط مرزی تعیین می‌شود. برای بهتر روشن شدن مطلب، حلقه بسته ای را که یک ناحیه و سطح روی آن را مشخص می‌کند در نظر بگیریم.اگر داشته باشیم:

درون ناحیه${\displaystyle \nabla ^{2}\varphi =f}$ وروی سطح ${\displaystyle \varphi =g}$ در این صورت ${\displaystyle \varphi (x,y,z)}$ منحصربه‌فرد خواهد بود.

بیان دیگری از قضیه یکتایی به این صورت است که::دو پاسخ معادله لاپلاس که در شرایط مرزی یکسانی صدق کنند، یا با هم برابرند یا اختلافشان حداکثر یک عدد ثابت است.

بار نقطه ای در نزدیکی صفحه رسانا

مثال ساده ای برای روش بارهای تصویری همان مسئله بار نقطه ای در نزدیکی صفحه رساناست. بار نقطه ای q را به فاصله a از صفحه رسانای نامتناهی متصل به زمین در نظر بگیرید. می خواهیم بدانیم پتانسیل در بالای صفحه چقدر است. به علت القای بار الکتریکی توسط q روی صفحه، پتانسیل تنها پتانسیل ناشی از بار نقطه ای نخواهد بود. شرایط مرزی از این قرارند: در z=0 داریم ${\displaystyle \varphi =0}$ (صفحه رسانا به زمین متصل شده‌است.) وبرای نقاط دور ${\displaystyle \varphi =0}$ قضیه یکتایی تضمین می‌کند که اگر ما با هر شگردی پاسخی یافتیم که در شرایط مرزی صدق کرد، این تنها پاسخ موجود و جواب مورد نظر ما خواهد بود. حالا دو بار نقطه ای q ,q- را در مختصات z=a و z=-a قرار می‌دهیم و صفحه رسانا را حذف می‌کنیم. پتانسیل حاصل از این پیکر بندی در مختصات استوانه ای به این شکل است:

${\displaystyle V\left(\rho ,\varphi ,z\right)={\frac {1}{4\pi \epsilon _{0}}}\left({\frac {q}{\sqrt {\rho ^{2}+\left(z-a\right)^{2}}}}+{\frac {-q}{\sqrt {\rho ^{2}+\left(z+a\right)^{2}}}}\right)\,}$

که در z=0 و برای نقاط دور مقدار این پتانسیل صفر خواهد بود که این دقیقاً همان شرایط مرزی مورد نظر ماست. پس پیکر بندی جدید برای z>0 دارای پتانسیل پیکربندی نخست است.

چگالی بار سطحی روی سطح رسانا از رابطه

${\displaystyle \sigma =-\epsilon _{0}{\frac {\partial V}{\partial z}}{\Bigg |}_{z=0}\,}$

${\displaystyle \sigma =-\epsilon _{0}{\frac {\partial V}{\partial z}}{\Bigg |}_{z=0}={\frac {-qa}{2\pi \left(x^{2}+a^{2}\right)^{3/2}}}}$

در می آید.

حالا کل بار القایی روی سطح انتگرال تابع${\displaystyle \sigma }$ خواهد بود.این انتگرال گیری در مختصات کروی یا استوانه ای راحت‌تر خواهد بود.در مختصات استوانه ای داریم:

${\displaystyle x^{2}+y^{2}=\rho ^{2}}$

${\displaystyle Q_{t}\,}$	${\displaystyle =\int _{0}^{2\pi }\int _{0}^{\infty }\sigma \left(\rho \right)\,\rho \,d\rho \,d\theta \,}$
	${\displaystyle ={\frac {-qa}{2\pi }}\int _{0}^{2\pi }d\theta \int _{0}^{\infty }{\frac {\rho \,d\rho }{\left(\rho ^{2}+a^{2}\right)^{3/2}}}}$
	${\displaystyle =-q\,}$

که پاسخی است که انتظارش را داشتیم. میدان حاصل از این بار نقطه ای در نزدیکی صفحه رسانا را در تصویر ش 1 می‌بینید.

تعمیم

روش بارهای تصویری را می‌توان به حضور 2 یا تعداد بیشتری بار نقطه ای در نزدیکی رسانا تعمیم داد.که در این صورت صفحه با تصویر همه بارها جایگزین می‌شود.از آنجا که پتانسیل الکتروستاتیکی کل همان جمع نرده ای پتانسیل هاست، پس پتانسیل هر بار نقطه ای در محل صفحه با پتانسیل تصویرش خنثی می‌شود.ازین رو پتانسیل هر جایی در محل صفحه صفر خواهد بود، که همان شرایط مرزی مسئله ماست. در صورت وجود دو قطبی الکتریکی در فاصله a از صفحه، باید صفحه را با یک دو قطبی معکوس و متقارن واقع در a- جایگزین کنید.

روش بارهای تصویری برای کره رسانا

تصویر ش3.

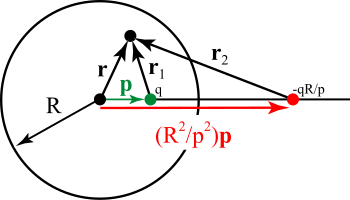
مسئله ای را در نظر بگیرید که در آن بار نقطه ای q در داخل کره رسانای متصل به زمین به شعاع R قرار دارد(ان بار در شکل با رنگ سبز نشان داده شده‌است).می خواهیم پتانسیل داخل کره را طور بدست بیاوریم که پتانسیل هر جایی روی کره صفر شود. دستگاه مختصات را به این صورت در نظر می‌گیریم که مبدأ مختصات در مرکز کره و بار q در فاصله p از مبدأ روی محور z قرار دارد.می خواهیم پتانسیل را در داخل کره در نقطه ای به فاصله r از مبدأ روی محور r بیابیم.شرط مرزی موجود این است که پتانسیل در ${\displaystyle |\mathbf {r} |=R}$ صفر باشد. از تقارن معلوم است که بار تصویری${\displaystyle q^{\prime }}$ باید روی محور z باشد.توجه کنید که بارهای تصویری همواره باید در خارج محلی که پتانسیل را در آن محاسبه می‌کنیم باشند.(بار تصویری در شکل با رنگ قرمز نشان داده شده‌است.) حالا پتانسیل حاصل از این دو بار در نقطه ای در درون کره به این صورت خواهد بود:

${\displaystyle \varphi (\mathbf {r} )={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{|\mathbf {r} -\mathbf {p} |}}+{\frac {q^{\prime }}{|\mathbf {r} -\mathbf {z} |}}\right]}$

می خواهیم در${\displaystyle |\mathbf {r} |=R}$ پتانسیل صفر باشد.بردار یکانی در راستی محور r را${\displaystyle \mathbf {\hat {r}} }$و در راستای محورz را ${\displaystyle \mathbf {\hat {z}} }$در نظر می‌گیریم.

${\displaystyle \varphi (\mathbf {r} )={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{|r\mathbf {\hat {r}} -p\mathbf {\hat {z}} |}}+{\frac {q^{\prime }}{|r\mathbf {\hat {r}} -z\mathbf {\hat {z}} |}}\right]}$

در جمله اول در مخرج ازp و در جمله دوم از r فاکتور می‌گیریم و پتانسیل را درr=R مساوی صفر قرار می‌دهیم.

${\displaystyle \varphi (\mathbf {r} )={\frac {1}{4\pi \epsilon _{0}}}\left[{\frac {q}{p|{\frac {R}{p}}\mathbf {\hat {r}} -\mathbf {\hat {z}} |}}+{\frac {q^{\prime }}{R|\mathbf {\hat {r}} -{\frac {z}{R}}\mathbf {\hat {z}} |}}\right]=0}$

که می‌دهد:

${\displaystyle {\frac {q}{p}}={\frac {-q^{\prime }}{R}}}$و ${\displaystyle {\frac {R}{p}}={\frac {z}{R}}}$

یا

${\displaystyle q^{\prime }={\frac {-R}{p}}q}$و${\displaystyle z={\frac {R^{2}}{p}}}$

برای اینکه پتانسیل سطح کره به جای صفر هر ثابت دیگری مثل V باشد کافیست بار نقطه ای دیگری را در مر کز کره قرار دهیم.

حال می خواهیم بدانیم پتانسیل در نقاط خارج کره به چه صورت است. برای چگالی بارهای سطحی در مختصات قطبی کروی داریم:

${\displaystyle \sigma (\theta )=\epsilon _{0}{\frac {\partial \varphi }{\partial r}}{\Bigg |}_{r=R}}$

که با انتگرال‌گیری روی سطح کره می‌دهد:

Q=-q

که همان بار القایی روی سطح داخلی کره است.

منابع

• جکسون، جان دیوید.الکترودینامیک کلاسیک.ویرایش سوم 1998.تهران:گروه تخصصی آراکس.
• ریتس، میلفورد.مبانی نظری الکترو مغناطیس.ویرایش چهارم1388.
• Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. ISBN 0-13-805326-X.
• ویکی‌پدیای انگلیسی.