معمای مربع گم‌شده

به مربع خالی توجه کنید

معمای مربع گم‌شده معمایی متأثر از خطای دید است که در کلاس‌های درس ریاضیات به منظور به کارگیری تجسم هندسی دانش‌آموزان مطرح می‌شود.
این پازل دو ترکیب از اشکالی را نشان می‌دهد که ظاهراً در مجموع، دو مثلث قائم‌الزاویهٔ هم‌نهشت هستند. اما یکی از آن‌ها یک مربع ۱×۱ فضای خالی دارد.

پاسخ

تفاوت دو ترکیب

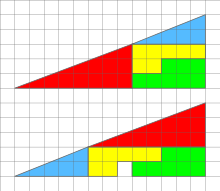
پاسخ:

قاعده مثلث آبی پنج واحد است و ارتفاع آن دو واحد،

در نتیجه سه واحد تا قاعده ی کلی فضا باقی می ماند، مساحت زیر مثلث آبی ۱۵ واحد می شود یعنی ۳×۵

اما اگر مثلث قرمز در بالا قرار بگیرد ، هشت واحد قاعده دارد و سه واحد ارتفاع در نتیجه ۱۶ واحد زیرش فضا باقی می گذارد، اما با ۱۵ واحد قبلی مساحت پر شده بود و یک واحد فضا باز می شود،

این دقیقا مثل چیدن یکسری اشیا بدون شکل داخل یک سطل است که هر چی مرتب تر قرار بدیم فضای بیشتری داریم،

در حالتی که یک واحد خالی می ماند در واقع بهتر چیدیم و فضای خالی ایجاد شده است اما در حالت اول به دلیل شلختگی کل فضا اشغال شده است، اینم به زبان ساده و خودمانی،

نویسنده: فرزاد فرخی آموزگار

دبستان غیردولتی پسرانه فرزاد ، شاهرود

معماهای مشابه

معمای مربع گم‌شده

نسخهٔ دیگری از این معما به چهار چهارضلعی و یک مربع کوچک در میان آن‌ها مربوط می‌شود که در کنار هم مربع بزرگ‌تری می‌سازند. هنگامی که چهارضلعی‌ها می‌چرخند فضای مربع کوچک را پر می‌کنند ولی به نظر می‌رسد مربع بزرگ بدون تغییر مانده است.

تجزیه سم لوید

مساحت مربع از مساحت مستطیل یک واحد کمتر است!

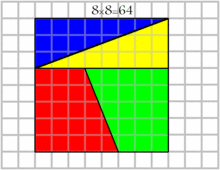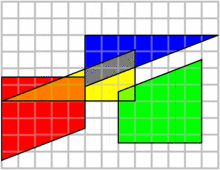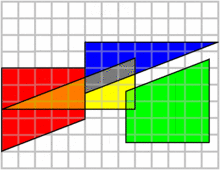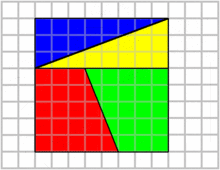
چهار قطعه با مجموع مساحت ۶۴ در کنار هم قرار گرفته‌اند ولی بعد از جابه‌جایی ۱ واحد به مساحت آن‌ها اضافه می‌شود در حالی که قطعات تغییری نکرده‌اند پس مساحت کل هم نباید تغییر می‌کرد!

علت این پدیده، شیب متفاوت قطعه‌ها است، برای مثال قطعه آبی و سبز در حالت دوم هم‌پوشانی دارند و قسمتی از هر کدام با هم منطبق می‌شوند. شیب وتر قطعه آبی برابر ۰٫۳۷۵ است که روی ضلعی از قطعه سبز قرار می‌گیرد که شیب آن ۰٫۴ است. نزدیکی شیب‌ها باعث می‌شود این تفاوت در نگاه اول نمایان نشود. برای درک بهتر کافیست شکل را روی کاغذ رسم کنید و قطعات را پس از برش جابه‌جا کنید.

این دوحالت با یک واحد اختلاف همیشه سه جمله ی متوالی دنباله ی فیبوناتچی را نشان میدهند که یکی از حالات ضرب دوجمله ی ${\displaystyle a_{n-1}}$ و ${\displaystyle a_{n+1}}$ و دیگری برابر ${\displaystyle (a_{n})^{2}}$ است. به عنوان مثال شکل روبرو دوحالت ${\displaystyle 5\times 13=65}$ و ${\displaystyle 8\times 8=64}$ که حاصل سه جمله ی متوالی دنباله ی فیبوناتچی هستند.

منابع

• مشارکت‌کنندگان ویکی‌پدیا. «Missing square puzzle». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۲ ژوئیه ۲۰۱۰.