مینیماکس
این مقاله نیازمند ویکیسازی است. لطفاً با توجه به راهنمای ویرایش و شیوهنامه، محتوای آن را بهبود بخشید. |
این مقاله نیازمند تمیزکاری است. لطفاً تا جای امکان آنرا از نظر املا، انشا، چیدمان و درستی بهتر کنید، سپس این برچسب را بردارید. محتویات این مقاله ممکن است غیر قابل اعتماد و نادرست یا جانبدارانه باشد یا قوانین حقوق پدیدآورندگان را نقض کرده باشد. |
مینیماکس یا کمینبیش[۱] یک قانون تصمیم سازی است که در نظریهٔ تصمیم، نظریهٔ بازیها، آمار و فلسفه برای کمینه کردن (مینیمم کردن) احتمال شکست و ضرر در بدترین حالت (بیشترین احتمال ضرر) از آن استفاده میشود. بهطور مشابه بیشینه کردن سود کمینه (ماکسمین) را نیز بیشینهٔ کمینه مینامیم. اساساً برای بازیهای دو نفرهٔ مجموعهٔ صفر در نظریهٔ بازیها فرمول بندی شدهاست که هم حرکتهای جایگزین (چند انتخابی) بازیکنها و هم حرکات همزمان انتخاب کردن بازیکنها را پوشش میدهد. این مفهوم را میتوانیم به بازیهای پیچیدهتر و تصمیم سازیهای غیر قطعی بسط دهیم.[۲][۳]
نظریهٔ بازیها
[ویرایش]در نظریهٔ بازیهای همزمان، استراتژی کمینه یک استراتژی مرکب است که قسمتی از حل بازی با مجموعهٔ صفر میباشد. در بازیهای مجموعهٔ صفر حل کمینه (مینیماکس) مشابه تعادل نش (نام دانشمند) است.[۴]
تئوری کمینهٔ بیشینه (مینیماکس)
[ویرایش]
حالتهای قضیهٔ مینیماکس (کمینهٔ بیشینه)
[ویرایش]برای هر دو نفر، بازی مجموعهٔ صفر با استراتژیهای متناهی بسیاری وجود دارد٬یک مقدار θ و استراتژی آمیخته برای هر بازیکن وجود دارد که:
الف) برای استراتژی در پیش گرفته شده توسط بازیکن دوم بهترین پرداخت ممکن برای بازیکن ۱، θ است.
ب) برای استراتژی در پیش گرفته شده توسط بازیکن اول بهترین پرداخت ممکن برای بازیکن ۲، θ- است.
معادلا استراتژی بازیکن ۱ برای او یک سودمندی (پرداخت)θ بدون در نظر گرفتن استراتژی بازیکن دوم تضمین میکند. بهطور مشابه بازیکن ۲ میتواند سودمندی θ- را برای خودش تضمین کند.
نام مینیماکس از جایی میآید که هر بازیکن سعی دارد تا بیشینه پرداخت محتمل برای طرف مقابل را کمینه کند. چون بازی مجموعهٔ صفر است او همچنین ماکزیمم ضرر خود را کمینه میکند (برای مثال مقدار کمینهٔ پرداختش را بیشینه میکند).
این قضیه اولین بار توسط جان فون نویمان در سال ۱۹۲۸ انتشار یافت، که از او نقل قول شدهاست: ” تا جایی که میبینم هیچ قضیهای از بازیها بدون این قضیه نخواهد بود. من فکر میکردم هیچ قضیهٔ با ارزشی انتشار نیافته تا زمانی که قضیه مینماکس (کمینهٔ بیشینه) اثبات شد! ” .
برای تعمیم میتوانید قضیهٔ مینماکس سیون - نام دانشمند - قضیهٔ پارتاساراتی را ببینید. هم چنین میتوانید مثالی از یک بازی بدون متغیر ببینید.
مثال پیش روبازی مجموعهٔ صفر است که A و B حرکات همزمان انجام میدهند و راه حل مینیماکس را نشان میدهد. فرض کنید هر بازیکن ۳ انتخاب دارد و ماتریس پرداخت برای A در سمت راست نمایش داده شد است. ماتریس پرداخت B را هم مانند ماتریس پرداخت A با علامت معکوس در نظر بگیرید. (برای مثال اگر انتخاب بازیکنها A۱ و B۱ باشد، B باید ۳ تا به A بپردازد) سپس انتخاب کمینهٔ بیشینه برای A ٬A۲ است زیرا در بین بدترینها بهترین انتخاب این است که باید ۱ بپردازد. در حالی که انتخاب کمینهٔ بیشینه برای B٬B۲ است زیرا در بهترین حالت که کمترین ضرر را میکند این است که چیزی نپردازد. با این وجود این راه حل پایدار نیست زیرا اگرBبداند که A٬A۲ را انتخاب میکند، سپس B ٬B۲ را انتخاب میکند تا ۱ سود کند. هم چنین اگر A باور داشته باشد که B٬B۲ را انتخاب میکند او هم A۱ را انتخاب میکند تا ۳ واحد سود ببرد. اما پس از آن B٬B۲ را انتخاب میکند و به همین ترتیب هر دو بازیکن سختی تصمیمگیری را میفهمند. به همین دلیل به استراتژی پایدارتری نیاز است.
بعضی انتخابها توسط دیگر انتخابها مغلوب میشوند و میتوانند حذف شوند: A, A۳ را انتخاب نخواهد کرد. زیرا انتخاب هر کدام از A۱ و A۲ نتیجهٔ بهتری خواهد داشت بدون اینکه انتخاب B اهمیت داشته باشد. همچنین B3,B را انتخاب نخواهد کرد زیرا ترکیباتی از B۲ و B۱ صرف نظر از اینکه A چه انتخابی دارد، نتیجهٔ بهتری خواهد داشت.
A با انتخاب A۱ با احتمال ۶/۱ و، A۲ با احتمال ۶/۵ از پرداخت مورد انتظار بیش از ۳/۱ جلوگیری خواهد کرد.
پرداخت مورد انتظار برای A، ۳*(۱/۶)-۱*(۵/۶)=-۱/۳ خواهد بود برای زمانی که B ٬B۱ را انتخاب میکند و -۲*(۱/۶)+۰*(۵/۶)=-۱/۳ خواهد بود برای زمانی که B, B۲ را انتخاب میکند.
مشابها زمانی که B استراتژی B۱ را با احتمال ۳/۱ و استراتژی B۲ با احتمال ۳/۲ بدون در نظر گرفتن انتخاب A انتخاب میکند، میتواند مطمئن باشد که حداقل دارای سود مورد انتظار ۳/۱ خواهد بود.
این استراتژی مرکب پایداری دارد و اثبات شدنی نیست.
بیشینهٔ کمینه (ماکسمین)
[ویرایش]متعاقباً در نظریه بازیها کمینه بیشینه (مینیماکس) از بیشینهٔ کمینه (ماکسمین) متمایز است. مینیماکس در بازیهای مجموعهٔ صفر استفاده میشود و مینیمم کردن پرداخت ماکسیمم حریف را نشان میدهد که در بازیهای مجموعهٔ صفر معادل با مینیمم نمودن ماکزیمم ضرر خودش و ماکسیمم کردن مینیمم سود خودش میباشد.
ماکسیمین عبارتیست که عموماً برای بازیهای با مجموعهٔ غیر صفر برای توصیف استراتژی که ماکسیمم میکند پرداخت مینیمم خودش را استفاده میشود. در بازیهای با مجموع غیر صفر عموماً مشابه مینیمم کردن ماکسیمم سود حریف و مشابه استراتژی تعادل نش نیست.
نظریهٔ بازیهای ترکیبیاتی
[ویرایش]در نظریهٔ بازیهای ترکیبیاتی الگوریتم مینیماکسی برای راه حلها ی بازی وجود دارد.
یک نسخهٔ ساده از الگوریتم مینیماکس که در زیر توضیح داده شده با بازیهایی شبیه تیک تاک توی (بازی شبیه دوز) سرو کار دارد که هر بازیکن میتواند ببرد، ببازد یا مساوی کند. اگر بازیکن A در یک حرکت بتواند ببرد این بهترین حرکت او خواهد بود. اگر بازیکن B بداند که حرکت او میتواند بازی را به موقعیتی ببرد که بازیکن A را در شرایطی قرار دهد که در یک حرکت ببرد، در حالی که با حرکتی دیگر میتواند بازیکن A را در موقعیتی قرار دهد که در بهترین حالت با B مساوی کند برای بازیکن B حرکت دوم بهترین خواهد بود. به آسانی میتوان بهترین حرکت را پیدا کرد.
الگوریتم مینیماکس با حرکت عقبگرد از آخر بازی به پیدا کردن بهترین حرکت کمک میکند. در هر مرحله فرض میتوان که بازیکن A سعی دارد شانس پیروزی خود را ماکزیمم کند در حالی که در نوبت بعدی بازیکن B سعی دارد تا شانس پیروزی A را مینیمم کند (یعنی بازیکن B شانس پیروزی خودش را ماکسیمم میکند).
الگوریتم مینیماکس با حرکتهای جایگزینی
[ویرایش]یک الگوریتم مینیماکس یک الگوریتم بازگشتی برای انتخاب حرکت بعدی در یک بازی n نفری است که معمولاً بازیها دو نفره است. هر مقدار، به هر موقعیت یا مکان از بازی وابسته است. این مقدار بوسیلهٔ تابع ارزیابی موقعیت محاسبه میشود و مطلوبیت رسیدن به آن موقعیت را برای یک بازیکن نشان میدهد. سپس بازیکن مینیمم مقدارهای نتایج موقعیتهای احتمالی حاصل ٬از حرکتهای پیش روی حریف را ماکزیمم میکند. اگر نوبت حرکت A باشد A به هر حرکت مجاز در آن موقعیت یک مقدار میدهد.
یک روش تخصیص ممکن شامل اختصاص دادن یک برد مشخص برای A مانند ۱ و برای B مانند -۱ میباشد. این منتهی میشود به تئوری بازیهای ترکیبیاتی که بوسیلهٔ جان هورتون کانوی توسعه داده شده. یک جایگزین از قانونی استفاده میکند که اگر نتیجهٔ یک حرکت یک برد فوری برای A باشد یک مقدار متناهی مثبت را به متغیر جایگزینی اختصاص میدهد و اگر یک برد فوری برای B باشد یک مقدار متناهی منفی را اختصاص میدهد. مقدار A از هر حرکت دیگری، مینیمم مقداری که از هر پاسخ محتمل B نتیجه شده میباشد. به این دلیل A را بازیکن حداکثری و B را بازیکن حداقلی مینامند؛ بنابراین نام این الگوریتم مینیماکس است. در الگوریتم بالا یک مقدار مثبت یا منفی متناهی به هر کدام از موقعیتها اختصاص داده خواهد شد. به همین خاطر مقدار هر موقعیت مقدار موقعیت پیروزی یا شکست نهایی خواهد بود. اغلب این تنها احتمالی است که در انتهای هر بازی پیچیده مثل شطرنج رخ میدهد. زیرا به صورت محاسباتی، عملی نیست که تا انتهای بازی در پیش بگیریم، مگر به سمت انتهای بازی و به موقعیتهای به جای آن، مقدارهای متناهی داده میشود که تخمین زده میشود که کدام بازیکن میبرد.
این میتواند توسعه داده شود، اگر بتوانیم یک تابع ارزیابی اکتشافی نگه داریم که مقدارهایی را به حالتهای غیر نهایی بازی بدون در نظر گرفتن دنبالهٔ کامل احتمالی میدهد. سپس میتوانیم الگوریتم مینیماکس را محدود کنیم تا فقط به یکسری حرکات مشخص پیش رو نگاه کنیم. به این عدد، عدد پیشبینی میگویند که با “تاو”(پایلز) اندازهگیری میشود.
این الگوریتم میتواند به عنوان جستجوی راسهای یک درخت بازی در نظر گرفته شود. ضریب انشعاب مفید برای درخت، میانگین بچههای هر راس است (برای مثال میانگین حرکات مجاز در یک موقعیت). تعداد راسهایی که میتوان جستجو کرد معمولاً به صورت نمایی با عدد پای افزایش میابد. (اگر حرکتهای اجباری یا موقعیتهای تکراری ارزیابی شود، کمتر از نمایی است) تعداد راسهایی که برای تحلیل یک بازی جستجو میشود حدوداً ضریب انشعاب است که به سمت قدرت تعداد پایها افزایش میابد و این غیر عملی است که بازی مانند شطرنج را بهطور کامل با الگوریتم مینیماکس تحلیل کنیم.
کارایی الگوریتم سادهٔ مینیماکس احتمالاً بهطور چشمگیری بدون تأثیر روی نتیجه با استفاده از هرس آلفا بتا پیشرفت میکند. روش هرس ابتکاری دیگر هم میتواند استفاده شود اما تضمینی وجود ندارد که همهٔ آنها نتیجهای مشابه جستجوی غیر هرسی (un-pruned) دهد.
یک الگوریتم مینیماکس ساده میتواند بهطور واضحی اصلاح شود تا علاوه بر نمرهٔ مینیماکس، کل تنوع اصلی را هم برگرداند.
شبه کد
[ویرایش]شبه کدی برای الگوریتم مینیماکس با عمق محدود در زیر آورده شده.
function minimax(node, depth, maximizingPlayer)
if depth = 0 or node is a terminal node
return the heuristic value of node
if maximizingPlayer
bestValue := -∞
for each child of node
val := minimax(child, depth - 1, FALSE))
bestValue := max(bestValue, val);
return bestValue
else
bestValue := +∞
for each child of node
val := minimax(child, depth - 1, TRUE))
bestValue := min(bestValue, val);
return bestValue
(* Initial call for maximizing player *)
minimax(origin, depth, TRUE)
کد c++
[ویرایش]//vector<int>adj[MAX_Size];
int minimax(int node,int depth,bool maximizingPlayer){
if(depth== 0||adj[node].size() ==1)return val[nod];//adj%5Bnode].size()==1 mean the node is a Leaf
if(maximizingPlayer==1){
int bestValue=-INF;
for(int i=0;i<adj[node].size();i++){
val=minimax(child,depth-1,0);
bestValue=max(bestValue,val);
}
return bestValue;
}
else{
int bestValue=+INF;
for(int i=0;i<adj[node].size();i++){
val=minimax(child,depth-1,1);
bestValue=max(bestValue,val);
}
return bestValue;
}
}
//(* Initial call for maximizing player *)
//minimax(origin, depth, TRUE)
مینیماکس بهطور جداگانه با هر کدام از دو بازیکن در کد برخورد میکند. با توجه به اینکه، مینیماکس به الگوریتم نگاماکس ساده میشود.
فرض کنید در یک بازی، در هر نوبت، هر بازیکن حداکثر دو گزینه برای حرکت بعدی خود پیش رو داشته باشد. الگوریتم ارائه شده درختی را مانند شکل زیر تولید میکند که در آن دایرهها نمایانگر حرکتهای بازیکنی است که الگوریتم را اجرا میکند (بازیکن حداکثری) و مربعها نمایانگر حرکتهای بازیکن مقابل (بازیکن حداقلی) میباشد. همانطور که توضیح داده شد به دلیل محدودیت منابع محاسباتی، درخت در هر مرحله فقط ۴ حرکت را پیشبینی میکند.
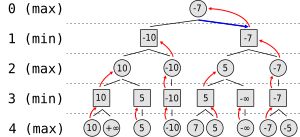
درخت از یک تابع اکتشافی استفاده میکند. حرکتهایی که به برد بازیکن با مقدار حداکثر منجر میشود با مثبت بینهایت مشخص شدهاند و حرکتهایی که باعث برد بازیکن با مقدار حداقل میشود با منفی بینهایت نشان داده شدهاست. برای مثال در سطر ۳ مقدار هر گره برابر مینیمم مقادیر فرزندان آن گره خواهد بود. برای مثال سمت چپترین گره در سطر سوم باید مینیمم بین ۱۰ و مثبت بینهایت را به عنوان مقدار خود انتخاب کند بنابراین مقدار این گره ۱۰ خواهد شد.
مرحلهٔ بعدی بدست آوردن مقادیر گرههای سطر دوم است که در این مرحله هر گره مقداری برابر با ماکسیمم مقادیر فرزندان خود خواهد داشت. به همین صورت این الگوریتم کار خود را ادامه میدهد و به صورت یک در میان ماکسیمم مقادیر فرزندان و مینیمم آنها را به گره اختصاص میدهد تا این که به ریشهٔ درخت برسیم که در این مرحله باید ماکسیمم مقادیر فرزندان را به گره اختصاص دهیم (که در شکل با فلش آبی رنگ مشخص شدهاست) و این همان حرکتی است که بازیکن به منظور به حداقل رساندن انتخابهای حداکثری طرف مقابل باید انجام دهد.
مینیماکس و عدم قطعیت
[ویرایش]زمانی که بازیکن دیگری وجود نداشته باشد، نظریهٔ مینیماکس تصمیمگیری را هم در بر میگیرد ولی در این حالت دنبالهٔ تصمیمگیریها بر اساس حقایق و اتفاقات ناشناخته و نامعلوم میباشند. برای مثال تصمیمگیری برای اکتشاف یک معدن مستلزم صرف هزینهای است که در صورتی که مواد معدنی موجود نباشند این هزینه هدر رفتهاست ولی در صورت وجود این مواد این هزینه کاملاً بهصرفه است و موجب سودآوری میگردد. یک راه برای رویارویی با این مسئله این است که به آن به عنوان یک بازی با طبیعت نگاه کنیم و با ایدهای شبیه به چیزی که در قانون مورفی وجود دارد جلو برویم و از همان تکنیکهایی استفاده کنیم که در بازی «دو نفر با مجموع صفر» استفاده میکردیم.
مینیماکس در نظریهٔ تصمیم آماری
در نظریهٔ تصمیم آماری کلاسیک یک برآورد گر δ داریم که برای تخمین پارامتر θ از آن استفاده میکنیم. همچنین تابع ریسک
R(θ,δ) را معمولاً به عنوان انتگرال تابع شکست در نظر میگیریم و محاسبه میکنیم در صورتی که شرایط زیر برآورده شود δ̅ را مینیماکس مینامیم:
نظریهٔ تصمیمگیری غیر احتمالی
[ویرایش]یکی از ویژگیهای اصلی تصمیمگیری مینیماکس غیر احتمالی بودن آن است که در آن بر خلاف تصمیمگیریهایی که بر اساس مقادیر قابل انتظار و سودهای قابل پیشبینی انجام میشود، هیچ پیش فرضی راجع به احتمال وقوع پیشامدهای مختلف نداریم و صرفاً یک تحلیل از پیشامدهای ممکن را در نظر میگیریم و از آن استفاده میکنیم بنابراین در این روش در مقایسه با سایر تکنیکهای تصمیمگیری میتوانیم راحتتر فرضیاتمان را تغییر دهیم.
کاربردهای زیادی از این روش غیر احتمالی وجود دارد که از جملهٔ مهمترین آنها میتوان به تاسف مینیماکس و نظریهٔ تصمیمگیری شکاف اطلاعات اشاره کرد.
علاوه بر این مینیماکس تنها به اندازهگیریهای ترتیبی (که در آن نتایج بتوانند با یکدیگر مقایسه شوند) احتیاج دارد و در آن هیچ احتیاجی به اندازهگیریهای فاصلهای نیست (که در آن نتایج شامل این هستند که این روش تا چه میزان بهتر یا بدتر از روشهای دیگر است) و در نهایت یک دادهٔ ترتیبی را به عنوان خروجی میدهد.
نتیجهای که از یک تحلیل مینیماکس به دست میآید به ما میگوید که آیا استراتژی مورد بحث مینیماکس است یا خیر، بدترین حالت و نتیجهٔ آن چیست و این که در بین بدترین نتایج کدام یک نسبت به بقیه کمتر بد است که در مقایسه با تحلیلهایی که بر اساس مقادیر قابل انتظار انجام میشود که در آنها نتیجه به این صورت است که به ما میگوید که استراتژی مورد بحث به E(x)=n منجر میشود روش مینیماکس شفافتر است و از آن میتوانیم برای دادههای ترتیبی استفاده کنیم.
منابع
[ویرایش]- ↑ «کمینبیش» [اقتصاد] همارزِ «minimax»؛ منبع: گروه واژهگزینی. جواد میرشکاری، ویراستار. دفتر سیزدهم. فرهنگ واژههای مصوب فرهنگستان. تهران: انتشارات فرهنگستان زبان و ادب فارسی (ذیل سرواژهٔ کمینبیش)
- ↑ Bacchus, Barua (January 2013). Provincial Healthcare Index 2013 (PDF) (Report). Fraser Institute. p. 25.
- ↑ Professor Raymond Flood. Turing and von Neumann (video). Gresham College – via YouTube.
- ↑ Maschler, Michael; Solan, Eilon; Zamir, Shmuel (2013). Game Theory. Cambridge University Press. pp. 176–180. ISBN 9781107005488.