پل خربگیری

پل خربگیری یا پونس اسینوروم (لاتین: Pons asinorum) پنجمین قضیه در مقالهٔ اول اصول اقلیدس است و بیان میکند که زوایای مقابل به ساق مثلث متساویالساقین با هم برابرند. عکس این قضیه هم درست است، یعنی اگر دو زاویهٔ مثلثی با هم مساوی باشند اضلاع متقابل آن زوایا هم با هم مساویاند.
عنوان این قضیه اشاره به این موضوع دارد که این قضیه اولین مسئله نسبتاً دشوار در اصول اقلیدس است و بسیاری از افراد آن را درک نمیکردند و با رسیدن به آن، همچون خری که روی پل مانده باشد، دیگر جلو نمیرفتند. این عبارت امروزه به ضربالمثلی تبدیل شده و به مسئله یا چالشی اشاره دارد که محکی برای جداسازی متخصصان و مجربها از مبتدیان است.
اثبات
[ویرایش]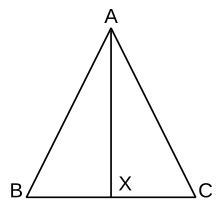
اگر ABC مثلثی متساویالساقین باشد، دو ساق آن، یعنی AC و AB برابرند. مراد این است که ثابت شود دو زاویهٔ قاعده این مثلث، یعنی زاویههای C و B، برابرند.
برهان قضیه با ترسیم خط AX، که زاویه A را نصف میکند، آغاز میشود.
درستی این مرحله از کار بدین خاطر است که اقلیدس پیشتر نشان دادهاست که هر زاویه ای را میتوان نصف کرد؛ بنابراین، C را نیز میتوان به دو قسمت مساوی تقسیم کرد.
با ترسیم خط AX مثلث ABC به دو مثلث AXC و AXB تقسیم میشود. در مورد این دو مثلث اخیر میدانیم که:
اولاً AC با AB برابر است، زیرا گفته بودیم که مثلث نخستین، یعنی مثلث ABC، متساویالساقین است.
ثانیاً زاویه CAX مساوی با زاویه BAX است، زیرا AX نیمساز زاویه است.
ثالثاً از آن جا که AX بین دو مثلث کوچکتر مشترک است، این ضلع آن دو مثلث برابرند.
بنابراین میتوانیم حکم کنیم که دو مثلث AXC و AXB همنهشت هستند، زیرا پیش از قضیه مورد بحث در کتاب اصول قضیهای هست که حکم میکند هر دو مثلثی که دو ضلع و زاویه بین آنها از یکی با دو ضلع و زاویه بینشان از دیگری برابر باشند همنهشت اند، و از آن جا که دو مثلث مورد بحث چنین قسمتهای برابری دارند، همنهشت هستند.
سرانجام میتوان حکم کرد که زاویه B مساوی زاویه C است، زیرا بنا به تعریف مثلثهای هم نهشت بخشهای متناظر مساویند و زاویههای C و B چنین بخشهایی هستند. به این ترتیب، قضیه مورد بحث با چند دلیل استنتاجی که هر یک از آنها فرضی بیتردید را به خدمت میگیرد و نتیجهای بی تردید را به بار میآورد، ثابت میشود.
اثبات اقلیدس و پروکلس
[ویرایش]
اثبات این قضیه در اصول اقلیدس نتیجهٔ دیگری نیز دارد و آن این است که اگر ساقها را امتداد دهیم زوایای میان قاعده و امتداد ساقها نیز با هم برابر میشوند.
فرض میکنیم ABC مثلث متساوی الساقین با ساقهای AB و AC باشد؛ و خطهای راست BD و CE به ترتیب امتدادهای AB و AC باشند.
میگوییم که زاویهٔ ABC با زاویهٔ ACB برابر است، و زاویهٔ CBD با زاویهٔ BCE.
نقطهٔ دلخواه F را بر BD انتخاب میکنیم؛ و بر AE که بزرگتر است AG را برابر با خط کوچکتر AF جدا و F را به C و G را به B وصل میکنیم.
در این صورت چون AF با AG مساوی است و AB با AC، و ضلعهای FA و AC نیز به ترتیب با ضلعهای GA و AB مساوی اند؛ بنابراین دو مثلث AFC و AGB، که در زاویه FAG مشترک اند، با هم مساوی میشوند، پس قاعدهٔ FC با قاعدهٔ GB برابر میشود. از تساوی همین در مثلث زوایای متناظر آنها، یعنی زاویههای رو به رو به اضلاع متساوی نیز با هم مساوی خواهند شد، یعنی زاویهٔ ACF با زاویه ABG و زاویهٔ AFC با زاویه AGB. و چون تمام AF با تمام AG مساوی است، و در آنها AB مساوی است با AC، پس بقیه BF با بقیه CG مساوی میشود. اما ثابت شده بود که FC هم با GB مساوی است؛ بنابراین دو ضلع BF و FC به ترتیب با دو ضلع CG و GB مساوی هستند؛ و زاویهٔ BFC هم با زاویه CGB مساوی است، بنابراین مثلث BFC و مثلث CGB همنهشتند، و بقیهٔ زاویههای رو به رو به ضلعهای متساوی با هم مساوی میشوند، یعنی زاویهٔ FBC با زاویه GCB و زاویهٔ BCF با زاویهٔ CBG. از این رو، چون تساوی تمامی زاویهٔ ABG با تمامی زاویهٔ ACF ثابت شده بود، و در این زاویهها زاویهٔ CBG با زاویهٔ BCF مساوی بود، لذا زاویه ABC با زاویهٔ ACB مساوی میشود؛ و این دو زاویه زاویههای مجاور به قاعدهٔ مثلث ABC هستند. اما تساوی زاویهٔ FBC هم با زاویه GCB ثابت شده بود که زاویههای زیر قاعده هستند.


اثبات پاپوس
[ویرایش]پاپوس اثبات دیگری برای قضیه بیان میکند که کوتاهتر از اثبات اقلیدس است و نیازی به ترسیمات اضافی ندارد ولی بغرنجتر است. اثبات او بدین قرار است: فرض کنیم مثلث ABC متساوی الساقین باشد و AB و AC ساقهای آن باشند. مثلثهای ABC و ACB را در نظر بگیرید. ACB مثلث دیگری است به طوری که هر کدام از نقاط A , B ,C به ترتیب متناظر با نقاط A,C,B در مثلث ABC هستند. پس زاویهٔ A در هر دو مشترک است و پاره خطهای AB از مثلث ABC با پاره خط AC از مثلث ACB برابر است و پاره خطهای AB از مثلث ACB با پاره خط AC از مثلث ABC برابر است. پس دو مثلث به حالت دو ضلع و زاویه بین با هم همنهشتند. از آنجایی که در دو مثلث همنهشت، زوایای متناظر با هم برابرند. پس زاویۀ B با C برابر است.
منابع
[ویرایش]- مشارکتکنندگان ویکیپدیا. «Pons asinorum». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۵ نوامبر ۲۰۱۸.