گرادیان کاهشی

کاهش گرادیان (انگلیسی: Gradient descent) الگوریتم بهینه‌سازی مرتبهٔ اول از نوع الگوریتم‌های تکرار شونده است. برای یافتن کمینهٔ محلی یک تابع با استفاده از این الگوریتم، گام‌هایی متناسب با منفی گرادیان (یا گرادیان تخمینی) تابع در محل فعلی برداشته خواهد شد. اگر در استفاده از این الگوریتم، گام‌هایی متناسب با جهت مثبت گرادیان برداشته شود، به بیشینهٔ محلی تابع نزدیک می‌شویم که به این فرایند افزایش گرادیان گفته می‌شود. اگر تابع محدب یا مقعر باشد به بیشینه جهانی می‌رسیم.^[۱] بسیاری از مسائل یادگیری ماشینی محدب هستند و ازین رو گرادیان کاهشی جواب بهینه را در این مسائل تولید می‌کند.^[۱]

توضیح الگوریتم

فرض می‌کنیم تابعی چند متغیره به اسم ${\displaystyle F(\mathbf {x} )}$داریم که مشتق‌پذیر است و هدف یافتن یک نقطه ${\displaystyle x}$ است که تابع را به حداقل ممکن برساند. برای نقطه ${\displaystyle a}$ جهتی که مقدار تابع با بیشترین شیب به صورت محلی کاهش پیدا می‌کند، خلاف جهت گرادیان تابع در آن نقطه یعنی بردار ${\displaystyle -\nabla F(\mathbf {a} )}$است.

الگوریتم گرادیان کاهشی به صورت متناوب هر بار مقداری در خلاف جهت گرادیان حرکت می‌کند به این معنی که ${\displaystyle \mathbf {a} _{n+1}=\mathbf {a} _{n}-\gamma \nabla F(\mathbf {a} _{n})}$. در اینجا ${\displaystyle \gamma }$ مقداری است که هربار الگوریتم در خلاف جهت گرادیان حرکت می‌کند. معمولاً این مقدار بسیار کوچک است.

برای توابع محدب هر بار مقدار تابع یا کمتر می‌شود یا ثابت می‌ماند به این معنی که${\displaystyle F(\mathbf {a} _{0})\geq F(\mathbf {a} _{1})\geq F(\mathbf {a} _{2})\geq \cdots }$

با نزدیک شدن به نقطه بهینه، از آنجا که گرادیان به صفر نزدیک می‌شود مقادیر ${\displaystyle a_{n}}$به ثبات می‌رسند و تغییر محسوسی نمی‌کنند.

توضیح ساده

تصور کنید در حال اسکی بازی هستید! هر چقدر شیب بیشتر باشد، در هر لحظه طول بیشتری را لیز خواهید خورد! در روش نزول شیب، هر چه شیب بیشتر باشد، طول گام در جهت مخالف بیشتر خواهد شد. دربارهٔ پرسپترون یک لایه:

${\displaystyle \Delta w=-\eta {\frac {\partial {\mathcal {E}}}{\partial w}}}$

مثال

فرض کنید می‌خواهیم کمینه تابع ${\displaystyle f(x_{1},x_{2})=(1-x_{1})^{2}+100\times (x_{2}-{x_{1}}^{2})^{2}}$را با استفاده از الگوریتم کاهش گرادیان پیدا کنیم.

گرادیان این تابعِ دومتغیّریه این بردار است:

${\displaystyle \nabla f(x_{1},x_{2})={\begin{bmatrix}-2\times (1-x_{1})-400\times (x_{2}-{x_{1}}^{2})\times x_{1}\\200\times (x_{2}-{x_{1}}^{2})\end{bmatrix}}}$

معادله الگوریتم گرادیان کاهشی به شکل پایین خواهد بود، برای ${\displaystyle \gamma }$مقدار ${\displaystyle 0.1}$ را در نظر گرفته‌ایم، ${\displaystyle {\begin{bmatrix}x_{1}^{n}\\x_{2}^{n}\end{bmatrix}}}$ ورودی در مرحله ${\displaystyle n}$ است و ${\displaystyle {\begin{bmatrix}x_{1}^{n+1}\\x_{2}^{n+1}\end{bmatrix}}}$ ورودی در مرحله ${\displaystyle n+1}$ است:

${\displaystyle {\begin{bmatrix}x_{1}^{n+1}\\x_{2}^{n+1}\end{bmatrix}}={\begin{bmatrix}x_{1}^{n}\\x_{2}^{n}\end{bmatrix}}-0.1\times {\begin{bmatrix}-2\times (1-x_{1}^{n})-400\times (x_{2}^{n}-{x_{1}^{n}}^{2})\times x_{1}^{n}\\200\times (x_{2}^{n}-{x_{1}^{n}}^{2})\end{bmatrix}}}$

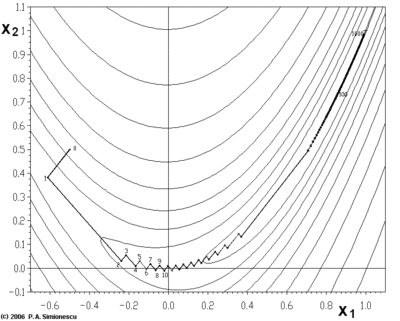
این الگوریتم را می‌توانیم با شکل پایین به تصویر بکشیم.

جستارهای وابسته

• روش گرادیان همیوغ
• روش بی‌اف‌جی‌اس
• روش نلدر - مید
• تقویت گرادیان
• رگرسیون خطی
• رگرسیون لجیستیک

منابع

1. Kim, Donghwan; Fessler, Jeffrey (2015-10-17). "Optimized first-order methods for smooth convex minimization". Mathematical Programming (به انگلیسی). 159 (1–2): 81–107. ISSN 0025-5610. PMID 27765996.

• مشارکت‌کنندگان ویکی‌پدیا. «Gradient descent». در دانشنامهٔ ویکی‌پدیای انگلیسی، بازبینی‌شده در ۲۳ ژانویه ۲۰۱۷.

پیوند به بیرون