Le Sagen gravitaatioteoria

Le Sagen gravitaatioteoria on gravitaation syytä koskeva kineettinen teoria, jonka esitti ensimmäisenä Nicolas Fatio de Duillier vuonna 1690 ja myöhemmin Georges-Louis Le Sage vuonna 1748. Teorian mukaan gravitaatio aiheutui kaikkialla liikkuvista pienistä näkymättömistä hiukkasista, joita Le Sage nimitti ultramundaanisiksi korpuskeleiksi ja jotka törmäisivät kaikkiin kappaleisiin kaikista suunnista. Tämän mallin mukaan mitkä tahansa kaksi kappaletta ikään kuin varjostavat toisiaan vähentämällä tällaisten hiukkasten virtaa tietystä suunnasta, jolloin niitä osuu samaan kappaleeseen eri suunnista eri määrä, mikä aiheuttaa kappaleita toisiaan kohti työntävän nettovoiman. Tämä gravitaation mekaaninen selitys ei koskaan tullut yleisesti hyväksytyksi, vaikka fyysikot toisinaan pohtivat sitä 1900-luvun alkuun saakka, jolloin sitä yleensä alettiin pitää jo lopullisesti kumottuna.

Teorian perusteet

P1: Yksinäinen kappale
Ei nettovoimaa mihinkään suuntaan

Teorian mukaan gravitaatiovoima aiheutuu pienistä hiukkasista, joita liikkuu suurella nopeudella kaikkiin suuntiin kaikkialla avaruudessa. Hiukkas­virran oletetaan olevan yhtä suuri kaikkiin suuntiin, joten niitä osuu eristettyyn kappaleeseen A yhtä paljon kaikista suunnista, niin että siihen vaikuttaa vain sen sisään suuntautuva paine mutta ei kappaletta mihinkään suuntaan työntävää voimaa (P1).

P2: Kaksi kappaletta "vetää" toisiaan puoleensa

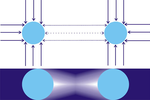
Kun toinen kappale B on läsnä, se pysäyttää osan niistä hiukkasista, jotka muuten osuisivat kappaleeseen A kappaleen B suunnasta, joten tästä suunnasta kappaleeseen A osuu vähemmän hiukkasia kuin vastakkaisesta suunnasta. Samoin kappaleeseen B osuu vähemmän hiukkasia kappaleen A suunnasta kuin vastakkaisesta suunnasta. Voidaan sanoa, että kappaleet A ja B "varjostavat" toisiaan, ja kappaleet työntyvät toisiaan kohti, koska hiukkasten niihin kohdistamat voimat ovat epätasapainossa (P2). Täten kappaleiden välinen näennäinen vetovoima johtuukin tämän teorian mukaan itse asiassa siitä, että toisen kappaleen suunnasta kappaleeseen kohdistuu pienempi työntövoima.

Törmäysten luonne

P3: Vastakkaiset virrat

Jos kappaleen A ja siihen osuvien gravitaatiota aiheuttavien hiukkasten törmäykset ovat täysin kimmoisia, siitä kimmonneiden hiukkasten intensiteetti on yhtä suuri kuin sitä kohti tulevienkin, joten tuloksena ei ole kappaletta mihinkään suuntaan kuljettavaa voimaa. Samoin on laita, vaikka toinen kappale B olisikin lähellä, sillä B toimii kilpenä kappaletta A kohti kulkevia hiukkasia vastaan. Hiukkanen C, joka muuten osuisi kappaleeseen A, pysähtyy kappaleeseen B, mutta toinen hiukkanen D, joka muuten ei olisi osunut kappaleeseen A, kimpoaa kappaleesta B siihen suuntaan ja siten korvaa C:n. Niinpä jos törmäykset ovat täysin kimmoisia, kappaleiden A ja B heijastamat hiukkaset kumoaisivat täysin varjostusvaikutuksen. Jotta tuloksena olisi gravitaation kaltainen voima, on siis oletettava, että törmäykset eivät ole täysin kimmoisia, tai ainakin, että heijastuneet hiukkaset liikkuvat hitaammin eli niiden liikemäärä on törmäyksen jälkeen pienempi. Tämä johtaisi hiukkasvirtaan, jonka liikemäärä kappaleesta A poispäin on pienempi kuin kappaletta A kohti tulevien hiukkasten liikemäärä, niin että tuloksena olisi kappaletta A kohti suuntautuva kokonaisliikemäärä (P3). Jos näin oletetaan, kahden kappaleen tapauksessa heijastuneiden hiukkasten liikemäärä ei täysin kumoa varjostusilmiötä, koska heijastunut virta on alkuperäistä pienempi.

Käänteisen neliön laki

P4: Käänteisen neliön laki

Koska on oletettu, että kappale joko absorboi kaikki gravitaatiota aiheuttavat hiukkaset tai hidastaa niiden liikettä, tästä seuraa, että hiukkasvirta massiivisesta kappaleesta poispäin on pienempi kuin sitä kohti. Voimme kuvitella, että tämä hiukkasvirtojen epätasapaino – ja sen vuoksi siitä aiheutuva, lähellä olevaan kappaleeseen kohdistuva voima – olisi jakautunut pallopinnalle, jonka keskipiste on kappaleessa (P4). Hiukkasvirtojen epätasapaino koko pallopinnalla ei riipu pallon koosta, kun taas pallon pinta-ala on suoraan verrannollinen sen säteen neliöön. Tämän vuoksi hiukkasvirtojen epätasapaino pinta-alayksikköä kohti pienenee kääntäen verrannollisena etäisyyden neliöön.

Verrannollisuus massaan

Edellä esitetyistä perusteista seuraisi, että voima on suoraan verrannollinen kappaleen pinta-alaan. Newtonin gravitaatiolain mukaan gravitaatio on kuitenkin verrannollinen massaan. Jotta tämä voitaisiin selittää Le Sagen teorian avulla, on oletettava, että 1) aineen perushiukkaset ovat hyvin pieniä, niin että suuret ainekappaleet ovat suurelta osin tyhjää tilaa, ja b) että hiukkaset ovat niin pieniä, että aineellinen kappale pysäyttää niistä vain pienen osan. Tästä seuraa, että kappaleen aiheuttama "varjostus" on verrannollinen aineen perushiukkasten yhteenlaskettuun pinta-alaan. Jos lisäksi oletetaan, että aineen kaikki perushiukkaset ovat samanlaisia ja erityisesti, että niillä tiheyden suhde pinta-alaan on sama, tästä seuraa, että varjostusilmiö on ainakin likimäärin verrannollinen kappaleen massaan (P5).

Fatio

Nicolas Fatio

Nicolas Fatio esitti gravitaatiota koskevien ajatustensa ensimmäisen muotoilun kirjeessään Christiaan Huygensille keväällä 1690.^[1] Kaksi päivää myöhemmin Fatio luki kirjeensä Royal Societyn tilaisuudessa Lontoossa. Seuraavina vuosina Fatio laati useita käsikirjoituksia pääteoksestaan De la Cause de la Pesanteur, mutta mitään hänen kirjoituksistaan ei hänen elinaikanaan julkaistu. Vuonna 1731 Fatio myös lähetti teoriansa, kirjoitettuna latinankieliseksi runoksi Lucretiuksen tyyliin, Pariisin tiedeakatemialle, mutta se hylättiin. Eräät katkelmat näistä käsikirjoituksista sekä kopio runosta päätyi myöhemmin Georges-Louis Le Sagen haltuun, joka kuitenkaan ei löytänyt niille julkaisijaa.^[2] Niinpä kesti vuoteen 1929 saakka,^[3] ennen kuin Karl Bopp julkaisi Fation käsikirjoituksen ainoan täydellisen kopion, ja vuonna 1949^[4] Gagnebin rekonstruoi Le Sagen hallussa aikoinaan olleiden paperien perusteella Fation alkuperäisen artikkelin. Gagnebinin laatimassa muodossa teksti sisälsi lisäyksiä ja muutoksia, jotka Fatio oli tehnyt tekstiinsä vielä vuonna 1743, neljäkymmentä vuotta sen jälkeen, kun hän oli kirjoittanut sen version, johon Bopp oli julkaissut. Kuitenkin Boppin version jälkipuoliskolla ovat Fation teorian matemaattisesti kehittyneimmät osat, joita ei ollut Gagnebinin julkaisemassa versiossa.

Fation teoria

Fation pyramidi (ongelma I)

P6: Fation pyramidi

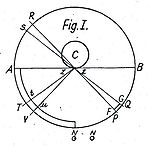
Fatio oletti, että maailmankaikkeus on täynnä hyvin pieniä hiukkasia, joita kulkee suurella nopeudella suoraviivaisesti kaikkiin suuntiin. Selventääkseen ajatuksiaan hän käytti seuraavaa esimerkkiä: Oletetaan kappale C, jonka pinnalle on piirretty äärimmäisen pieni pinta zz ja pallo, jonka keskipiste on pinnalla zz. Tämän pallon sisään Fatio sijoitti pyramidin PzzQ, jonka läpi jotkin hiukkaset virtaavat pintaa zz kohti ja jotkin, jotka ovat jo kimmonneet kappaleesta C, myös poispäin pinnasta zz. Fatio ehdotti, että kimmonneiden hiukkasten keskimääräinen nopeus on pienempi kuin pintaa kohti tulevien ja sen vuoksi myös niiden liikemäärä on pienempi. Tuloksena on nettovirtaus, joka työntää kaikkia kappaleita kohti pintaa zz. Siten toisaalta hiukkasvirta pysyy vakiona, mutta toisaalta lähellä pintaa zz tämä nettovirtaus kasvaa, ja sen vuoksi sen intensiteetti on verrannollinen etäisyyden neliöön 1/r². Ja koska Cn ympärille voidaan piirtää äärettömän monta tällaista pyramidia, tämä verrannollisuus pätee kaikkialla kappaleen C ympärillä.

Pienentynyt nopeus

Oikeuttaakseen oletuksen, että törmäyksen jälkeen hiukkasten nopeus on pienempi, Fatio teki seuraavat lisäoletukset:

• Joko tavallinen aine tai gravitaation aiheuttavat hiukkaset ovat kimmottomia, tai
• törmäykset ovat täysin kimmoisia, mutta hiukkaset eivät ole täysin kovia, ja sen vuoksi ne joutuvat törmäyksen jälkeen värähdystilaan, ja/tai
• kitkan vuoksi hiukkaset alkavat pyöriä törmäysten jälkeen.

Nämä ovat Fation teorian vaikeatajuisimpia kohtia, koska hän ei koskaan selvästi ilmaissut, minkälaatuista törmäystä hän piti todennäköisimpänä. Kuitenkin teoriansa viimeisessä versiossa vuodelta 1742 hän lyhensi tätä koskevia kohtia ja esitti hiukkasten kokevan "täysin kimmoisen tai joustavan voiman", kun taas tavallinen aine ei ollut täysin kimmoista, minkä vuoksi hiukkaset kimpoaisivat alkuperäistä pienemmällä nopeudella. Lisäksi Fatio kohtasi toisen ongelman: mitä tapahtuu hiukkasten törmätessä toisiinsa? Kimmottomat törmäykset saisivat niiden nopeuden pienenemään, minkä vuoksi painovoima vähitellen heikkenisi. Ratkaistakseen tämän ongelman Fatio ehdotti, että hiukkasten läpimitta on hyvin pieni niiden välisiin etäisyyksiin verrattuna, minkä vuoksi niiden väliset törmäykset olisivat hyvin harvinaisia.

Tiivistyminen

Fatio oli pitkään sitä mieltä, että koska hiukkaset lähestyvät aineellisia kappaleita nopeammin kuin poistuvat niiden luota heijastuttuaan, niitä vähitellen kertyisi aineellisten kappaleiden ympärille yhä enemmän. Tätä ilmiötä hän kutsui "kondensaatioksi", tiivistymiseksi. Myöhemmin hän kuitenkin päätyi siihen, että vaikka saapuvat hiukkaset ovat nopeampia, ne ovat kauempana toisistaan kuin heijastuneet, minkä vuoksi virta kumpaankin suuntaan on yhtä suuri. Tämän vuoksi hiukkaset eivät kasaannu minnekään, vaan heijastuneiden hiukkasten tiheys pysyy vakiona (edellyttäen että ne ovat niin pieniä, ettei niiden välisiä törmäyksiä tapahdu massiivisen kappaleen lähellä merkittävästi enemmän). Mikä merkittävämpää, Fatio havaitsi myös, että kasvattamalla sekä hiukkasten nopeutta että niiden kimmoisuutta voidaan saapuvien ja heijastuneiden hiukkasten nopeusero ja sen mukaisesti ero tiheyksien välillä saada kuinka pieneksi tahansa, ja silti tuloksena voitaisiin saada sama gravitaatioilmiö.

Aineen huokoisuus

P7: Kidehila (ikosaedri)

Jotta tuloksena saatava nettovoima olisi verrannollinen kappaleen massaan, Fatio oletti, että tavallinen aine päästää lävitseen suurimman osan niistä hiukkasista, jotka aiheuttavat gravitaatioilmiön. Hän esitti kolme mallia oikeuttaakseen tämän otaksuman:

• Hän otaksui, että aine koostuu pienistä palloista, joiden läpimitta on äärimmäisen pieni verrattuna niiden väliseen etäisyyteen. Tämän ehdotuksen hän kuitenkin hylkäsi, koska sen mukaan nämä osasetkin lähestyisivät toisiaan eivätkä kappaleet pysyisi vakaina.
• Toinen otaksuma oli, että nämä pallot eli atomit olisivat jonkinlaisten palkkien tai tankojen välityksellä yhteydessä toisiinsa ja muodostaisivat jonkinlaisen kidehilan. Kuitenkin hän hylkäsi myös tämän mallin – jos useammat atomit olisivat tällä tavoin sidoksissa toisiinsa, hiukkasvirta ei pääsisi aineen läpi yhtä suurelta osin kaikkiin suuntiin eikä tuloksena syntyvä voima olisi verrannollinen kappaleen massaan.
• Lopulta Fatio hylkäsi mallistaan pallot ja jätti vain tankojen verkon. Olettamalla ne äärettömän pieniksi verrattuina niiden välisiin etäisyyksiin voitiin saada suurin mahdollinen läpäisykyky.

Hiukkasten aiheuttama paine (ongelma II)

Jo vuonna 1690 Fatio oletti, että hiukkasten tasaiseen pintaan aiheuttama työntävä voima on kuudesosa siitä mikä se olisi, jos kaikki hiukkaset osuisivat siihen kohti­suorasti. Fatio todisti tämän ehdotuksensa määrittämällä voiman, jonka aiheuttavat tiettyyn pisteeseen zz osuvat hiukkaset. Hän johti kaavan p=ρv²zz/6. Tämä ratkaisu on hyvin samanlainen kuin Daniel Bernoullin kineettisessä kaasu­teoriassaan vuonna 1738 esittämä kaava p=ρv²/3. Tämä oli ensimmäinen kerta, jolloin kineettisen teorian kanssa analoginen ratkaisu esitettiin – kauan ennen kuin kineettisen kaasu­teorian perusteet esitettiin. Bernoullin antama arvo on kuitenkin kaksi kertaa nin suuri kuin Fation, mikä Zehen mukaan aiheutui siitä, että Fatio oletti hiukkasten liikemäärän muutoksen törmäyksessä olevan niiden massan ja nopeuden tulo, mv, vaikka jos törmäys on kimmoinen, liikemäärän muutos on kaksinkertainen, 2mv. Fation tulos olisi oikea vain täysin kimmottomien törmäysten tapauksessa. Fatio yritti käyttää ratkaisuaan, paitsi gravitaation, myös kaasujen käyttäytymisen selittämiseen. Hän yritti rakentaa lämpömittarin, joka osoittaisi ilmamolekyylien liiketilan ja siten arvioisi lämpö­tilan. Kuitenkaan Fatio, toisin kuin Bernoulli, ei samastanut lämpöä ilmahiukkasten liikkeeseen – hän käytti toista fluidia, joka aiheuttaisi tämän ilmiön. Ei myöskään tiedetä, vaikuttiko Fatio Bernoulliin vai ei.

Äärettömyys (ongelma III)

Tässä kappaleessa Fatio käsittelee äärettömyyden käsitettä ja sen merkitystä teorialleen. Fatio oikeutti monet otaksumuksensa sillä, että jokin ilmiö on "äärettömän paljon pienempi tai suurempi" kuin jokin toinen, niin että monet ongelmat voidaan saada merkityksettömän pieniksi. Esimerkiksi tankojen läpimitta on "äärettömän paljon" pienempi kuin niiden välinen etäisyys, tai hiukkasten nopeus on "äärettömän paljon" suurempi kuin tavallisen aineen, tai saapuvien ja heijastuneiden hiukkasten nopeusero on "äärettömän pieni."

Väliaineen vastus (ongelma IV)

Tämä on Fation teorian matemaattisesti monimutkaisin osa. Hän yritti arvioida hiukkasvirtojen liikkuville kappaleille aiheuttavan vastuksen. Oletetaan, että u on tavallisen aineen ja v gravitaation aiheuttavien hiukkasten nopeus ja ρ väliaineen tiheys. Fatio väitti, että mikäli v << u ja ρ on vakio, on hiukkasten aiheuttama vastus ρu². Jos taas v >> u ja ρ on vakio, on vastus 4/3ρuv. Newton kuitenkin oli osoittanut, että jos kiertoliikkeeseen ei kohdistu vastusta, on avaruudessa oltava äärimmäisen vähän ainetta. Tämän vuoksi Fatio oletti väliaineen tiheyden olevan hyvin pieni ja väitti, että jotta se voisi aiheuttaa havaitun gravitaation, tiheyden pienuus on kompensoitava hiukkasten suurella nopeudella, joka on "suoraan verrannollinen niiden tiheyden neliöjuureen". Tämä seuraa siitä, että Fation hiukkasten aiheuttaman paineen voidaan osoittaa olevan verrannollinen lausekkeeseen ρv². Zehen mukaan Fation yritys kasvattaa nopeus v hyvin suuriin arvoihin jättää vastuksen hyvin pieneksi verrattuna gravitaatioon, koska Fation mallissa hiukkasten aiheuttama vastus on verrannollinen suureeseen ρuv, mutta niiden aiheuttama paine, joka ilmenee gravitaationa, on verrannollinen lausekkeeseen ρv².

Fation teorian vastaanotto

Fatio oli kirjeenvaihdossa eräiden aikansa kuuluisimpien tiedemiesten kanssa. Monia hänen teorialleen esitettyjä vastaväitteitä voidaan nykyisin, pimeää ainetta ja maailmankaikkeuden metristä laajenemista koskevien teorioiden perusteella, pitää riittämättöminä, mutta kuitenkaan Fation teoriaa kohtaan ei nykyisin ole osoitettu sanottavaa mielenkiintoa.

P8: Edmond Halleyn, Christiaan Huygensin ja Isaac Newtonin allekirjoitukset Fation käsikirjoituksessa

Isaac Newton ja Fatio tapasivat toisensa henkilökohtaisesti useita kertoja vuosien 1690 ja 1693 välillä. Newtonin Fation teoriaa koskeneet kommentit vaihtelivat suuresti. Esimerkiksi, selvitettyään mitä gravitaation mekaaninen selittäminen välttämättä edellyttäisi, hän kirjoitti vuonna 1692 omaan Principian kopioonsa julkaisemattoman huomautuksen: Ainoa hypoteesi, jolla gravitaatio voidaan selittää, on kuitenkin tätä laatua, ja sen esitti mitä lahjakkain geometrikko Mr. N. Fatio.^[5] Toisaalta Fatio itse totesi, että vaikka Newton olikin yksityisesti sanonut Fation teorian olevan gravitaation paras mahdollinen mekaaninen selitys, hän myös mainitsi, että Newton itse taipui ajattelemaan, että gravitaation todellinen syy ei ollut mekaaninen. Myös David Gregory mainitsi "Memoranda"ssaan: "Newton ja Halley nauravat Fation tavalle selittää gravitaatio."^[5]

Christiaan Huygens oli ensimmäinen, jolle Fatio kertoi teoriastaan, mutta ei koskaan hyväksynyt sitä. Fatio uskoi, että hän oli saanut Huygensin vakuuttuneeksi teorian risti­riidatto­muudesta, mutta Huygens kiisti tämän eräässä kirjeessään Gottfried Leibnizille. Fatio kävi itse myös Leibnizin kanssa lyhyen kirjeenvaihdon teoriastaan. Leibniz arvosteli teoriaa siitä, että se edellytti hiukkasten välille tyhjää tilaa, minkä hän itse hylkäsi filosofisin perustein. Jakob Bernoulli osoitti kiinnostusta Fation teoriaa kohtaan ja pyysi Fatiota kirjoittamaan ajatuksensa gravitaatiosta täydelliseksi käsikirjoitukseksi, minkä Fatio todella tekikin. Bernoulli teki käsikirjoituksesta kopion, joka nykyisin on Baselin yliopiston kirjastossa ja joka oli Boppin toimittaman painoksen perustana.

Fation teoria ei kuitenkaan tullut yleisemmin tunnetuksi hänen elinaikanaan, koska hän ei koskaan sitä julkaissut ja joutui itse "ranskalaisiksi fanaatikoiksi" kutsuttujen, kamisardeihin kuuluvien uskonnollisten fanaatikkojen vaikutuksen alaiseksi, minkä vuoksi hän menetti maineensa.

Cramer ja Redeker

Vuonna 1731 sveitsiläinen matemaatikko Gabriel Cramer julkaisi väitöskirjan,^[6] jonka lopussa esiteltiin lyhyesti Fation esittämän kaltainen teoria – mukaan luettuna aineen verkkorakenne, analogia valon kanssa ja varjostus – mutta mainitsematta Fation nimeä. Fatio tiesi, että Cramerilla oli hallussaan kopio hänen alkuperäisestä käsikirjoituksestaan, ja niinpä hän syytti Crameria siitä, että hän vain toisti hänen teoriansa edes ymmärtämättä sitä. Cramer myös kertoi Fation teoriasta Le Sagelle vuonna 1749. Vuonna 1736 saksalainen lääkäri Franz Albert Redeker julkaisi myös samankaltaisen teorian.^[7] Ei tiedetä, oliko Redekerillä ja Fatiolla ollut mitään yhteyksiä toisiinsa.

Le Sage

Georges-Louis Le Sage

Le Sage esitti teoriansa ensimmäisen kerran Pariisin Tiedeakatemialle vuonna 1748 lähettämässään esseessä Essai sur l'origine des forces mortes, mutta sitä ei koskaan julkaistu.^[2] Omien sanojensa mukaan Le Sage kuuli Fation, Cramerin ja Redekerin teorioista vasta sen jälkeen, kun hän oli jo kirjoittanut ja lähettänyt esseensä. Ensimmäisen julkaistun version teoriastaan hän kirjoitti vuonna 1756^[8] ja vuonna 1758 hän laati siitä yksityiskohtaisemman esityksen Essai de Chymie Méchanique, jolla hän osallistui Rouenin tiedeakatemian järjestämään kilpailuun.^[9] Tässä esityksessään hän yritti selittää sekä gravitaation että kemiallisen affiniteetin. Laajemman yleisön ulottuville teoria tuli hänen artikkelissaan Lucrèce Newtonien vuodelta 1874, jossa sen vastaavuus Lucretiuksen käsitteiden kanssa oli täysin kehitetty.^[10] Uudemman kerran teorian julkaisu postuumisti Pierre Prévost vuonna 1818.^[11]

Le Sagen oletukset

P9: Le Sagen oma kaaviokuva ultramundaaneista korpuskeleista

Le Sage käsitteli teoriaa varsin yksityiskohtaisesti, ja hän esitti kvantitatiivisia arvioita eräille teorian parametreille.

• Hän kutsui gravitaation aiheuttavia hiukkasia ultramundaaneiksi korpuskeleiksi, koska hän oletti niiden olevan peräisin tuntemamme maailmankaikkeuden ulkopuolelta. Ultramundaanien korpuskelien virta on isotrooppinen eli yhtä suuri kaikkiin suuntiin, ja sen etenemisen lait ovat hyvin samanlaiset kuin valon.
• Le Sage väitti, että gravitaation kaltaista voimaa ei aiheutuisi, jos aineen ja näiden hiukkasten väliset törmäykset ovat täysin kimmoiset. Siksi hän oletti, että nämä hiukkaset, samoin kuin aineenkin pienimmät osaset, ovat "absoluuttisen kovia", ja väitti, että tästä seuraa muodoltaan monimutkainen vuorovaikutus siten, että törmäykset ovat täysin kimmottomia, jos hiukkanen osuu tavallisen aineen pintaan kohtisuorasti, mutta täysin kimmoisia, jos se osuu pintaan tangentiaalisesti. Tästä seurasi edelleen, että kimmonneiden hiukkasten keskimääräinen nopeus on 2/3 niiden alkuperäisestä nopeudesta. Jotta hiukkaset eivät törmäisi myös toisiinsa kimmottomasti, hän oletti niiden läpimitan olevan hyvin pieni verrattuna niiden väliseen etäisyyteen.
• Hiukkasvirran liikkuville kappaleille aiheuttama vastaus on verrannollinen tuloon uv, missä v on hiukkasten ja u liikkuvan kappaleen nopeus, kun taas gravitaatiovaikutus on verrannollinen hiukkasten nopeuden neliöön v², ja niinpä vastuksen ja gravitaation suhde voidaan saada kuinka pieneksi tahansa, kunhan vain v on tarpeeksi suuri. Tämän vuoksi hän arveli, että ultramundaaniset korpuskelit saattaisivat liikkua valon nopeudella, mutta myöhempien tarkastelujen perusteella hän päätteli niiden liikkuvan noin 10⁵ kertaa valoakin nopeammin.
• Jotta gravitaatiovaikutus saataisiin verrannolliseksi massaan, tavallisen aineen oletetaan koostuvan koppien kaltaisista rakenteista, joiden läpimitta on vain yksi 10⁷:sosa niiden välisestä etäisyydestä. Myös "tangot", joista kopit koostuvat, olivat ohuita verrattuna kopin läpimittaan, noin 10²⁰ kertaa niin pitkiä kuin ovat paksuja, joten hiukkaset voivat liikkua koppien läpi lähes esteettömästi.
• Le Sage yritti myös selittää koheesiovoimat ja erilaiset lujuusvoimat olettamalla, että oli olemassa useita erilaisia ja eri kokoisia ultramundaanisia korpuskeleja, kuten on esitetty kuvassa 9.

Le Sage väitti olevansa ensimmäinen, joka johti teorian kaikki seuraukset, ja myös Prévost sanoi, että Le Sagen teoria oli kehittyneempi kuin Fation.^[2] Kuitenkin vertailemalla teorioita keskenään ja analysoituaan yksityiskohtaisesti Fation artikkeleja (jotka olivat myös Le Sagen hallussa) Zehe väitti, ettei Le Sage lisännyt teoriaan mitään oleellisesti uutta eikä usein edes saavuttanut Fation tasoa.^[5]

Le Sagen teorian vastaanotto

Le Sagen ajatukset eivät saaneet laajaa kannatusta hänen aikanaan, lukuun ottamatta joitakuita hänen ystäviään ja tuttaviaan kuten Pierre Prévost, Charles Bonnet, Jean-André Deluc, Charles Mahon, kolmas Stanhopen jaarli, ja Simon Lhuilier. He mainitsivat Le Sagen teorian kirjoissaan ja artikkeleissaan ja kuvailivat sitä, ja niitä heidän aikalaisensa käyttivät Le Sagen teorian toissijaisina lähteinä.

Euler, Bernoulli ja Boscovich

Leonhard Euler totesi kerran, että Le Sagen malli oli "äärettömän paljon parempi" kuin kaikkien muiden kirjoittajien ja että kaikki mallille esitetyt vastaväitteet voidaan kumota, mutta myöhemmin hän sanoi, ettei analogia valon kanssa merkinnyt mitään, koska hän uskoi valon aaltoluonteeseen. Myöhempien tarkastelujensa perusteella Euler päätyi lopulta hylkäämään mallin ja kirjoitti Le Sagelle:^[12]

»Saatte antaa minulle anteeksi, jos tunnen suurta vastenmielisyyttä ultramundaanisia korpuskelejasi kohtaan, ja pidän parempana tunnustaa tietämättömyyteni gravitaation syistä kuin turvautua sellaisiin omituisiin hypoteeseihin.»

Daniel Bernoulli oli mieltynyt Le Sagen mallin ja hänen omien, kaasujen luonnetta koskevien ajatusten samankaltaisuuteen. Kuitenkin Bernoulli itse oli sitä mieltä, että hänen oma kineettinen kaasuteoriansa oli vain spekulaatiota, ja samoin hän piti Le Sagen teoriaa hyvin spekulatiivisena.^[13]

Roger Joseph Boscovich huomautti, että Le Sagen teoria oli ensimmäinen, joka tosiaan pystyi selittämään gravitaation mekaniikan avulla. Kuitenkin hän hylkäsi mallin, koska se edellytti suunnatonta ja muutoin käyttämätöntä määrää ultramundaanista ainetta. John Playfair kuvasi Boscovichin argumentteja seuraavasti:

»Suunnaton määrä atomeja, joiden kohtalona täten on jatkaa koskaan päättymätöntä matkaansa avaruuden äärettömyyden läpi, vaihtamatta kulkusuuntaansa ja palaamatta lähtöpaikkaansa, on otaksuma, jota ei ole sopusoinnussa luonnon yleisen taloudellisuuden kanssa. Mistä tulevat nämä lukemattomat virrat; eivätkö ne edellytä luovan voiman jatkuvaa toimintaa, joka on ääretön sekä paikallisen ulottuvuutensa että kestonsa osalta? ^[14]»

Hyvin samankaltaisen vastaväitteen esitti myöhemmin Maxwell (katso alempana). Lisäksi Boscovich kielsi kaiken suoran kosketuksen ja välittömän impulssin olemassaolon kokonaan ja väitti kaiken johtuvan työntävistä ja vetävistä kaukovaikutusvoimista.

Lichtenberg, Kant ja Schelling

Georg Christoph Lichtenberg ^[15] oppi tuntemaan Le Sagen teorian teoksesta Lucrece Netwonien ja eräästä Prévostin laatimasta yhteen­vedosta. Lichtenberg oli aluksi, Descartesin tavoin sitä mieltä, että kaikki luonnonilmiöt on selitettävä suora­viivaisten liikkeiden ja törmäysten avulla ja että Le Sagen teoria täytti nämä ehdot. Vuonna 1790 hän eräässä julkaisussaan ilmaisi innostuneensa teoriasta, uskoen että Le Sagen teoria käsittää kaiken tietomme asiasta ja tekee kaiken enemmän unelmoinnin asiasta hyödyttömäksi. Hän jatkoi sanomalla: "Jos se on uni, se on suurin ja suurenmoisin uni, joka on koskaan nähty..." ja että voimme täyttää sillä aukon kirjoissamme, jotka vain uni voi täyttää.^[16]

Hän viittasi usein Le Sagen teorioihin luennoillaan Göttingenin yliopistossa. Vuoden 1796 aikoihin hän kuitenkin muutti mieltään Immanuel Kantin vaikutuksesta, joka arvosteli jokaista teoriaa, joka yritti korvata vetävän voiman törmäyksillä.^[17] Kant huomautti, että jo avaruudellisen ulottuvuuden omaavien kappaleiden olemassa­olo, mukaan luettuna kaikki hiukkaset, joiden läpimitta ei ole nolla, edellyttää, että on olemassa jonkinlaisia sidos­voimia, jotka pitävät ulottuvaisen kappaleen osat kiinni toisissaan. Tätä voimaa ei voi selittää gravitationaalisten hiukkasten aiheuttamalla työntö­voimalla, koska niiden hiukkasten itsekin pitää pysyä koossa samanlaisen sidos­voiman vaikutuksesta. Välttääkseen tämän loogisen kehän Kant väitti, että on oltava olemassa perustavan laatuinen vetävä voima. Tämä oli aivan sama vastaväite, joka Descartesin impulssi­teoriaa vastaan oli aina esitetty edellisellä vuosi­sadalla, ja se oli saanut Descartesin seuraajatkin hylkäämään tämän osan hänen filosofiastaan.

Toinen saksalainen filosofi, Friedrich Wilhelm Joseph Schelling, hylkäsi Le Sagen mallin, koska sen mekanistinen materialismi oli vastoin Shellingin hyvin idealistista ja materialismin vastaista filosofiaa.^[18]

Laplace

Osittain Le Sagen teorian vuoksi Pierre-Simon Laplace yritti määrittää, kuinka nopeasti gravitaatiovaikutuksen on edettävä, jotta se olisi sopusoinnussa tähti­tieteellisten havaintojen kanssa. Hän laski, että nopeuden on oltava "ainakin sata miljoonaa kertaa suurempi kuin valon nopeus", jotta Kuun liikkeen aberraatiovaikutukset eivät aiheuttaisi liian suuria poikkeamia.^[19] Useimmat tutkijat, myös Laplace, katsoivat tämän tukevan Newtonin käsitystä välittömästä kauko­vaikutuksesta ja osoittavan kaikki Le Sagen esittämän tapaiset mallit epäuskottaviksi. Laplace väitti myös, että tällaisen mallin mukaan gravitaatio voisi olla verrannollinen massaan vain, jos Maan molekyylien ulko­pinnan ala oli enintään kymmenes­miljoonas­osa Maan pinta-alasta. Le Sagen pettymykseksi Laplace ei koskaan suoraan maininnut Le Sagen teoriaa omissa teoksissaan.

Kineettinen kaasuteoria

Koska Fation, Cramerin ja Redekerin teoriat eivät olleet laajalti tunnettuja, La Sagen versio teoriasta tuli uudestaan suuren mielen­kiinnon kohteeksi 1800-luvun jälki­puoliskolla, samaan aikaan kun kineettinen kaasuteoria kehittyi.

Leray

Jotta Le Sagen hiukkaset voisivat aiheuttaa tunnetun gravitaatio­ilmiön, niiden nopeuden on pienennyttävä niiden törmätessä tavalliseen aineeseen. Tästä kuitenkin seuraa, että hyvin suuren määrän niiden liike-energiaa on muututtava joksikin muuksi energian muodoksi. Ellei näillä hiukkasilla itsellään ollut keinoja varastoida sisäistä energiaa, tämän yli­jäämä­energian on muodossa tai toisessa varastoiduttava tavalliseen aineeseen. Käsitellessään tätä ongelmaa P. Leray^[20] ehdotti täysin samanlaista hiukkasmallia kuin Le Sage, mutta väitti lisäksi, että tämä aineeseen absorboitunut energia saa aikaan magnetismia ja lämpöä. Hän arveli, että tämä saattaisi selittää, mistä tähtien säteilemä energia tulee.

Kelvin ja Tait

William Thomson eli Lordi Kelvin.

Le Sagen teoria tuli uudestaan laajan mielenkiinnon kohteeksi sen jälkeen, kun William Thomson (lordi Kelvin) vuonna 1873 julkaisi sitä koskevan artikkelin.^[21] Toisin kuin Leray, joka käsitteli hiukkasten lämmittävää vaikutuksesta aiheutuvaa ongelmaa epä­täsmälli­sesti, Kelvin selitti, että absorboitunut energia vastaisi hyvin suurta lämpömäärää, joka riittäisi höyrystämään minkä tahansa kappaleen sekunnin murto-osassa. Niinpä Kelvin kehitti uudestaan ajatuksen, jonka jo Fatio oli esittänyt vuonna 1690 käsitelläkseen Le Sagen teoriaan liittyviä termo­dynaamisia ongelmia. Hän esitti, että ylimääräinen energia saattaisi absorboitua hiukkasten omiin sisäisiin energia­tiloihin, mikä perustui hänen esittämään teoriaan aineesta pyörteinä. Toisin sanoen, hiukkasten alkuperäinen etenemis­liikkeen energia siirtyisi samojen hiukkasten sisäisiin energia­tiloihin, etupäässä värähdys- ja pyörimis­liikkeen energiaksi. Viitaten Clausiuksen teoriaan, jonka mukaan kaasu­molekyylin jokaisen vapausasteen energia pyrkii kohti tiettyä osuutta kokonais­energiasta, Kelvin jatkoi olettamalla, että "energisoituneet" mutta hitaammin etenevät hiukkaset vähitellen saisivat takaisin alkuperäisen nopeutensa törmätessään kosmologisessa mittakaavassa toisiinsa. Kelvin piti myös mahdollisena, että ultra­mondaanisesta virrasta voitaisiin saada irti rajaton määrä vapaata energiaa ja kuvaili eräänlaista ikiliikkujaa, joka voisi saada sen aikaan. (Kelvinin päättelyssä oli kuitenkin se virhe, että Clausiuksen otaksuma pitäisi paikkansa vain, jos tavallinen aine olisi termo­dynaamisessa tasa­painossa ultra­mondaanisten virtausten kanssa, mutta siinä tapauksessa ne eivät saisi aikaan gravitaatio­vaikutusta.)

Myöhemmin Peter Guthrie Tait sanoi Le Sagen teoriaa ainoaksi uskottavaksi gravitaation selitykseksi, joka hänen aikaansa mennessä oli esitetty. Hän jatkoi sanomalla:

»Tämän merkillisin piirre on, että jos se on totta, se saa meidät todennäköisesti pitämään kaikkia energian lajeja viime kädessä liike-energiana.^[22]»

Kelvin itse ei kuitenkaan uskonut, että Le Sagen teoria lopulta voisi selittää ilmiöt onnistuneesti. Edellä mainitun, vuonna 1873 julkaisemansa artikkelin jälkeen hän ei koskaan palannut aiheeseen paitsi kirjoittaessaan seuraavan kommentin:

»Aineen kineettinen teoria on unelma eikä voi muuta ollakaan, ennen kuin se voi selittää kemiallisen affiniteetin, sähkön, magnetismin, gravitaation ja pyörrejoukkojen inertian. Le Sagen teoria yhdistettynä pyörreteoriaan voi ehkä selittää gravitaation ja sen suhteen massojen inertiaan, ellei esteenä olisi kiteiden oleellinen aelotropia ja gravitaation näköjään täydellinen isotropia. Mikään viitettä siitä, miten tämän ongelman yli voitaisiin päästä tai edes sivuta sitä, ei ole löydetty eikä kuviteltu, miten sellainen voitaisiin löytää.^[23] »

Preston

Samuel Tolver Preston^[24] osoitti, että monet Le Sagen hiukkasia koskevat oletukset, kuten niiden suoraviivainen liike ja vuorovaikutusten vähäisyys voitaisiin yhdistää oletukseksi, että kosmologisessa mittakaavassa ne käyttäytyisivät kuten kaasumolekyylit, joilla on äärimmäisen pitkä keskimääräinen vapaa matka. Preston hyväksyi myös Kelvinin ehdotuksen hiukkasten sisäisistä energiamoodeista. Hän kuvaili Kelvinin mallia vertaamalla sitä vertaamalla sitä teräsrenkaan ja alasimen väliseen törmäykseen – alasimeen törmäys ei sanottavasti vaikuta, mutta teräsrengas joutuisi värähdystilaan ja sen vuoksi jatkaisi liikettään pienemmällä nopeudella. Hän väitti myös, että hiukkasten keskimääräinen vapaa matka on vähintään planeettojen välisten etäisyyksien suuruinen – suuremmilla etäisyyksillä hiukkaset saisivat takaisin alkuperäisen etenemisliikkeensä energian törmätessään toisiinsa, minkä vuoksi hän myös päätteli, että hyvin suurilla etäisyyksillä kappaleiden välillä ei vaikuta vetovoimaa, olivatpa ne minkä kokoisia tahansa. Paul Drude arveli, että tämä voisi jotenkin liittyä Carl Gottfried Neumannin ja Hugo von Seeligerin teorioihin, joiden mukaan avoimessa avaruudessa gravitaatio hyvin suurilla etäisyyksillä tavalla tai toisella häviää.^[25]

Maxwell

James Clerk Maxwell

Encyclopædia Britannican yhdeksännessä painoksessa vuodelta 1875 James Clerk Maxwell julkaisi hakusanan atomi kohdalla katsauksen Kelvinin-Le Sagen teoriasta..^[26] Selitettyään teorian perusteet hän kirjoitti (Aronsonin käsityksen mukaan sarkastisessa mielessä:^[27]

»Tässä siis näyttää olevan tie kohti gravitaation selitystä, joka, jos sen voidaan osoittaa sopivan muissa suhteissa yhteen tosiasioiden kanssa, voi osoittautua kuninkaan tieksi tieteen todellisiin mysteereihin.»

Maxwell kommentoi Kelvinin ehdotusta hiukkasten erilaisista energiatiloista sanoen sen osoittavan, että gravitaation aiheuttavat hiukkaset eivät ole yksinkertaisia jakamattomia yksiköitä vaan pikemminkin systeemejä, joilla on omia sisäisiä energiatiloja ja joiden täytyy pysyä koosta jonkin selittämättömän vetovoiman ansiosta. Hän osoitti myös, että kappaleiden lämpötilan pitäisi pyrkiä kohti sitä arvoa, jossa molekyylien keskimääräinen liike-energia vastaisi ultramondaanisten partikkelien liike-energiaa ja osoitti, että jälkimmäisen on oltava paljon suurempi kuin edellisen, ja päätteli, että tavallisen aineen pitäisi palaa tuhkaksi sekunneissa Le Sagen pommitusten seurauksena. Hän kirjoitti:

»Olemme omistaneet tälle teorialle enemmän tilaa kuin se näyttäisi ansaitsevan, koska se on nerokas ja koska se on ainoa tähän mennessä kehitetty teoria gravitaation syystä, jota voidaan puolustaa ja vastustaa.»

Maxwell osoitti myös, että teoria edellyttää "suunnatonta määrää ulkoista voimaa" ja on sen vuoksi ristiriidassa energian säilymislain kanssa luonnon peruslakina. Preston väitti vastaan, että jokaisen yksittäisen hiukkasen liike-energia voisi olla kuinka pieni tahansa, jos sen massan oletetaan olevan tarpeeksi pieni ja vastaavasti hiukkasten lukumäärän tarpeeksi suuri. Tätä kuitenkin käsitteli myöhemmin yksityiskohtaisemmin Poincaré, joka osoitti, että Le Sagen mallin termodynaaminen ongelma oli edelleen ratkaisematta.

Isenkrahe, Ryšánek, du Bois-Reymond

Caspar Isenkrahe esitti oman mallinsa useissa julkaisuissa vuosien 1879 ja 1915 välillä. ^[28] Hänen perusolettamuksensa olivat hyvin samanlaiset kuin Le Sagen ja Prestonin, mutta hän sovelsi kineettistä teoriaa yksityiskohtaisemmin. Hänen oletuksensa, että hiukkasten nopeus törmäyksissä pienenisi ilman, että minkään muun kohteen energia kasvaisi, oli kuitenkin vastoin energian säilymislakia. Hän huomautti, että kappaleen paino ja tiheys liittyvät toisiinsa (koska mikä tahansa kappaleen tiheyden pieneneminen vähentäisi sen varjostusvaikutusta), ja näin hän päätyi esittämään, lämpölaajenemiseen liittyen, että kappaleet painaisivat lämpiminä enemmän kuin kylminä.

Myös Adalbert Ryšánek esitti vuonna 1887 ^[29] huolellisen analyysin, jossa sovellettiin myös Maxwellin lakia kaasumolekyylien nopeuksista. Hänen mukaansa oli olemassa erikseen gravitaatio- ja valoeetteri. Tämä kahden väliaineen erottaminen toisistaan oli välttämätöntä, koska hänen laskelmiensa mukaan se, ettei Neptunukseen kohdistunut mitään väliaineen vastusta, osoitti, että hiukkasten nopeuden oli oltava vähintään 5 · 10¹⁹ cm/s. Lerayn tavoin hänkin väitti, että absorboitunut energia muuttuisi lämmöksi, joka voisi kulkeutua valoeetterin mukana tai tähdet voisivat käyttää sen ylläpitääkseen energian tuotantoaan. Kuitenkaan näitä kvalitatiivisia otaksumia ei tukenut mikään kvantitatiivinen arvio tällä tavoin syntyvästä lämpömäärästä.

Vuonna 1888 Paul du Bois-Reymond väitti Le Sagen mallia vastaan muun muassa, että sen mukaan gravitaatio ei voisi olla tarkoin verrannollinen massaan. Jotta Newtonin teorian mukainen täydellinen verrannollisuus massaan saavutettaisiin, aineen olisi oltava rakenteeltaan äärettömän huokoista ja ultramondaanisen virtauksen intensiteetin äärettömän suuri. Du Bois-Reymond hylkäsi tällaiset otaksumat mielettöminä. Lisäksi hän huomautti Kantin tavoin, että Le Sagen teoria ei voinut saavuttaa tarkoitusperäänsä, koska se edellytti "kimmoisuuden" ja "absoluuttisen kovuuden" kaltaisia käsitteitä, jotka hänen mukaansa voitiin selittää ainoastaan vetävien voimien avulla. Sama ongelma koskee molekyylien välisiä koheesiovoimia. Tämän vuoksi tällaiset mallit eivät voi saavuttaa tarkoitustaan eli niiden avulla ei voida välttää olettamasta perustavan laatuisia vetäviä voimia.^[30]

Aaltomallit

Keller ja Boisbaudran

Vuonna 1863 F.A.E. ja Em. Keller^[31] esittivät teoriansa, joka muistutti Le Sagen teoriaa mutta jossa hiukkaset oli korvattu eetterissä etenevillä pitkittäisillä aalloilla. He olettivat, että sellaiset aallot leviäisivät kaikkiin suuntiin ja menettäisivät osan liike­määrästään osuessaan kappaleisiin, minkä vuoksi kappaleiden välissä niiden aiheuttama paine olisi pienempi kuin niiden ympärillä. Vuonna 1869 Paul-Émile Lecoq de Boisbaudran^[32] esitti saman mallin kuin Leray, mukaan luettuna absorption ja lämmön muodostumisen, mutta Kellerin tavoin hän korvasi hiukkaset pitkittäisillä aalloilla eetterissä.

Lorentz

Hendrik Antoon Lorentz

Näiden yritysten jälkeen muut kirjoittajat varsinkin 1900-luvun alussa korvasivat Le Sagen hiukkaset sähkö­magneettisella säteilyllä. Tämä liittyi varsinkin Lorentzin eetteri­teoriaan ja aika­kauden elektroniteoriaan, jossa aineen luonteen oletettiin olevan sähköinen.

Vuonna 1900 Hendrik Lorentz^[33] kirjoitti, ettei Le Sagen hiukkasteoriaa voitu sovittaa yhteen hänen aikansa elektroni­teorian kanssa. Mutta havainto, että sähkö­magneettiset aallot voivat aiheuttaa painetta, samoin kuin röntgensäteiden suuri läpäisykyky saivat hänet päättelemään, ettei ollut mitään estettä sille, ettei voisi olla vielä röntgensäteilyäkin läpitunkevampaa säteilyä, joka voisi korvata Le Sagen hiukkaset. Lorentz osoitti, että tästä tosiaan aiheutuisi vetävä voima varauksellisten hiukkasten välille, joita voidaan pitää aineen pienimpinä osina, mutta vain jos aaltojen energia absorboituisi kokonaan. Tämä oli sama perustava ongelma, joka oli vaivannut hiukkasmalleja. Niinpä Lorentz kirjoitti:

»Kuitenkin se seikka, että tämä vetovoima voisi esiintyä vain, jos tavalla tai toisella sähkö­magneettinen energia kokonaan häviäisi, on niin vakava vaikeus, että sitä, mitä edellä on sanottu, ei voi pitää hyvänä selityksenä gravitaatiolle. Eikä tämä ole ainoa mahdollinen vasta­väite. Jos gravitaation mekanismi muodostuu värähtelyistä, jotka kulkevat eetterin halki valon nopeudella, taivaan­kappaleiden liike muuttaisi niiden välistä veto­voimaa paljon suuremmassa määrin kuin tähti­tieteellisten havaintojen perusteella voidaan sallia.»

Vuonna 1922^[34] Lorentz ensin käsitteli Martin Knudsenin tutkimuksia harvennetuista kaasuista, ja samassa yhteydessä hän käsitteli Le Sagen hiukkasmallia ja sen jälkeen omaa sähkömagneettista malliaan, mutta päätyi samaan tulokseen kuin vuonna 1900: ilman absorptiota se ei voi aiheuttaa gravitaation kaltaista ilmiötä.

Vuonna 1913 David Hilbert viittasi Lorentzin teoriaan ja arvosteli sitä sillä perusteella, että mitään muotoa 1/r² olevaa voimaa ei voi syntyä, mikäli atomien välinen etäisyys on tarpeeksi suuri verrattuna aallonpituuteen.^[35]

J.J. Thomson

Vuonna 1904 J. J. Thomson^[36] käsitteli Le Sagen tyyppistä mallia, jossa ultramondaaninen virtaus muodostui hypoteettisesta, röntgensäteitäkin läpitunkevammasta säteilylajista. Hän esitti, että Maxwellin lämpöongelma voitaisiin välttää olettamalla, että absorboitunut energia ei muuttuisi lämmöksi vaan säteilisi pois jossakin vielä läpitunkevammassa muodossa. Hän esitti, että tämä prosessi voisi myös selittää radioaktiivisten aineiden säteilemän energian alkuperän, joskin hän piti todennäköisempänä, että energia tulisi näistä aineista itsestään. Vuonna 1911 Thomson palasi asiaan artikkelissaan "Matter" (aine) Encyclopædia Britannican 11. painoksessa.^[37] Siinä hän esitti, että tämä sekundaarisen säteilyn muoto olisi tavalla tai toisella analoginen sen kanssa, miten sähköiset hiukkaset kulkiessaan aineen läpi saavat sen lähettämään vielä läpitunkevampaa röntgensäteilyä. Hän huomautti:

»On hyvin mielenkiintoinen viimeaikaisten tutkimusten tulos, että mekanismi, jonka Le Sage otti käyttöön teoriaansa varten, on hyvin samankaltainen kuin mistä nyt on kokeellista näyttöä... Röngensäteet eivät kuitenkaan absorboituessaan saa aikaan vielä läpitunkevampaa röntgensäteilyä, joka voisi selittää vetovoiman, vaan joko vähemmän läpitunkevampaa tai alkuperäisen kaltaista säteilyä.»

Tommasina and Brush

Toisin kuin Lorentz ja Thomson, Thomas Tommasina^[38] esitti vuosien 1903 ja 1928 välillä, että pitkä­aaltoinen säteily selittäisi gravitaation ja lyhyt­aaltoinen aineen sisäiset koheesiovoimat. Vuonna 1911 myös Charles F. Brush^[39] ehdotti pitkä­aaltoista säteilyä. Mutta hän muutti myöhemmin mieltään ja ehdotti äärimmäisen lyhyttä aallon­pituutta.

Myöhempiä arviointeja

Darwin

Vuonna 1905 George Darwin laski, kuinka suuri kahden hyvin lähellä toisiaan olevan kappaleen välisen gravitaatiovoiman tulisi Le Sagen teorian mukaan olla, selvittääkseen, voisivatko geometriset syyt johtaa poikkeamiin Newtonin laista.^[40] Tässä Darwin korvasi Le Sagen teorian mukaisen aineen koppirakenteen mikroskooppisilla, yhtä suurilla kovilla palloilla. Hän päätteli, että Newtonin laki voisi päteä vain, jos törmäykset ovat täysin kimmottomia ja vahvisti täten, että Le Sagen teoria on termodynamiikan kannalta ongelmallinen. Lisäksi sellainen teoria voi olla pätevä vain jos sekä kohtisuorat että tangentiaaliset törmäykset ovat täysin kimmottomia, toisin kuin Le Sage oli väittänyt, ja jos aineen alkeishiukkaset ovat kaikki yhtä suuria. Hän sanoi edelleen, että valon emissio on täysin päinvastainen ilmiö kuin Le Sagen hiukkasten absorptio. Kappale, jonka pinnan lämpötila on eri kohdissa eri suuri, liikkuu kylmemmän osansa suuntaan. Eräässä myöhemmässä katsauksessaan Darwin esitti lyhyesti Le Sagen teorian ja sanoi tarkastelevansa sitä vakavasti, mutta kirjoitti sitten:

»En enää palaa tähän käsitykseen, paitsi sanoakseni, etten usko yhdenkään tiedemiehen olevan halukas hyväksymään, että se johtaisi oikealle tielle.^[41]»

Poincaré

Henri Poincaré

Henri Poincaré esitti vuonna 1908 merkittävän arvostelun, joka osittain perustui Darwinin laskelmiin.^[42] Hän päätteli, että vetovoima on verrannollinen lausekkeeseen ${\displaystyle S{\sqrt {\rho }}v}$, missä S on maan molekulaarinen pinta-ala, v hiukkasten nopeus ja ρ väliaineen tiheys. Laplacen tavoin hän päätyi siihen, että jotta veto­voima olisi verrannollinen kappaleen massaan, S voi olla enintään yksi kymmenes­miljoonas­osa Maan pinta-alasta. Toisaalta väliaineen vastus on verrannollinen lausekkeeseen Sρv, ja sen vuoksi vastuksen ja vetovoiman suhde on kääntäen verrannollinen lausekkeeseen Sv. Saadakseen vastuksen tarpeeksi pieneksi Poincaré laski, että hiukkasten nopeuden v olisi oltava vähintään 24 · 10¹⁷ kertaa valon nopeus. Kun täten on olemassa alarajat suureille Sv ja v ja yläraja pinta-alalle S, voidaan näiden avulla laskea, että törmäyksissä syntyvä lämpömäärä olisi verrannollinen lausekkeeseen Sρv³. Lasku osoittaa, että Maan lämpötilan tulisi nousta 10²⁶ celsiusasteta sekunnissa. Poincaré huomautti, että maa ei voisi kovin kauan pysyä nykyisen kaltaisena. Poincaré analysoi myös Tommasinan ja Lorentzin aaltomalleja todeten, että niihin liittyi sama ongelma kuin hiukkasmalliin. Jotta väliaineen vastus olisi tarpeeksi pieni, aaltojen nopeuden olisi oltava valon nopeutta suurempi, ja silti olisi sama lämpöön liittyvä ongelma. Kuvailtuaan mallin, jonka mukaan energia poistuu toisenlaisena säteilynä, hän päätyi toteamukseen: "Sellaisia ovat moni­mutkaiset hypoteesit, joihin päädytään, jos Le Sagen teoria yritetään pitää uskottavana."

Hän totesi myös, että jos Lorentzin mallissa absorboitunut energia muuttuisi kokonaan lämmöksi, Maan lämpö­tila nousisi 10¹³ astetta sekunnissa. Poincaré käsitteli Le Sagen teoriaa edelleen 1800- ja 1900-lukujen vaihteessa esittämänsä "uuden dynamiikan" yhteydessä, jossa hän myös tunnisti suhteellisuus­peri­aatteen. Hiukkasteorian osalta hän huomautti, että "on vaikea kuvitella törmäys­lakia, joka olisi sopusoinnussa suhteellisuus­peri­aatteen kanssa", ja vastukseen ja kuumenemiseen liittyvät ongelmat pysyivät.

Teorian ennusteet ja sille esitetyt vastaväitteet

Aine ja hiukkaset

Aineen huokoisuus

Eräs tämän teorian perustava ennuste on aineen äärimmäinen huokoisuus. Kuten Fatio ja Le Sage vuosina 1690 ja 1758 (ja jo ennen heitä Huygens) esittivät, aineen olisi koostuttava enimmäkseen tyhjästä tilasta siten, että hyvin pienet hiukkaset voisivat kulkea kappaleiden läpi lähes esteettömästi ja että sen vuoksi jokainen aineen osanen osallistuu gravitaatio­vuoro­vaikutukseen. Tämän ennusteen on myöhempi tutkimus joiltakin osin vahvistanut. Aine todella koostuu enimmäkseen tyhjästä tilasta, jota atomeissa on ytimen ja elektronien välissä, ja jotkin hiukkaset kuten neutriinot todella voivat kulkea aineen läpi lähes esteettömästi. Kuitenkaan alkeishiukkasia ei nykyisen tietämyksen perusteella voida enää pitää klassisen fysiikan mukaisina kappaleina, joiden vuorovaikutukset määräytyisivät niiden muodon ja koon mukaan (kuten Fation tai Le Sagen verkkorakenteen osat tai Isenkharen ja Darwinin pallot). Myöskään Lorentzin ja Thomsonin ehdotus, jonka mukaan sähköiset hiukkaset olisivat aineen perimmäisiä osasia, ei vastaa nykyisen fysiikan käsitystä.

Kosminen säteily

Le Sagen teoria kaikkine muunnelmineen edellyttää, että avaruus on kaikkialla täynnä kaikkiin suuntiin etenevää säteilyä, jolla on tavattoman suuri intensiteetti ja läpäisy­kyky. Tällä on joitakin yhtäläisyyksiä vuonna 1965 löydetyn kosmisen tausta­säteilyn kanssa. Kosmista tausta­säteilyä todella on kaikkialla ja se on lähes isotrooppista, mutta sen intensiteetti ja myös läpäisy­kyky ovat hyvin pienet. Neutriinojen virta, jollainen lähtee muun muassa auringosta, on Le Sagen ultra­mundaanisten korpuskelien tavoin hyvin läpäisy­kykyistä, mutta se ei ole iso­trooppista, koska sitä lähtee pää­asiassa tähdistä, ja sen intensiteetti on vielä pienempi kuin kosmisen tausta­säteilyn. Tietenkään sen enempää neutriinot kuin kosminen tausta­säteilykään eivät etene valoa nopeammin, niin kuin Le Sagen hiukkasilta olisi oletettava. Nyky­aikaiselta kannalta, vaikka hiukkasten ei Le Sagen tavoin ajateltaisikaan yksin­kertaisesti "työntävän" kappaleita, on Richard Feynman kuitenkin tutkinut oletusta, että neutriino tai jokin muu saman­kaltainen hiukkanen olisi kvanttigravitaatioteorian edellyttämä välittäjä­hiukkanen, mutta hän päätyi osoittamaan tämän teorian vääräksi.^[43]

Gravitaation varjostuminen

P10: Gravitaation varjostuminen

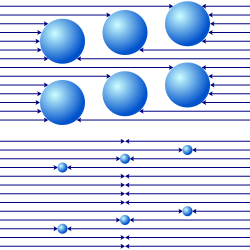
Vaikka Fation ja Le Sagen teorian mukaan aineen on oltava hyvin huokoista, oletetut hiukkaset eivät voi läpäistä sitä täydellisesti, koska siinä tapauksessa tuloksena ei olisi gravitaation kaltaista voimaa. Kuitenkin tämän läpäisy­kyvyn epä­täydellisyys johtaa ongelmiin: tarpeeksi suuren massan tapauksessa kahden kappaleen aiheuttama "varjostus" olisi pienempi kuin niiden varjostusten summa, jotka kumpikin aiheuttaisi erikseen, koska "varjot" sattuvat osittain päällekkäin (kuva P10 yllä). Tämä hypoteettinen ilmiö, jota on sanottu gravitaatiovarjostukseksi, johtaisi siihen, että gravitaatio ei olisi aivan suoraan verrannollinen kappaleiden massaan. Tämän vuoksi Fatio ja Le Sage olettivat, että varjostusilmiö oli niin pieni, ettei sitä havaita, minkä vuoksi vuorovaikutuksen vaikutusalan on oltava erittäin pieni (kuva P10, alla). Tämä seikka asettaa erittäin korkean alarajan hiukkasvirran intensiteetille, jotta se voisi saada aikaan havaitun gravitaation. Tämä gravitaatiovarjostus, missä muodossa tahansa, on myös ristiriidassa ekvivalenssiperiaatteen kanssa, jonka Eötvösin koe seuraajineen on osoittanut päteväksi hyvin suurella tarkkuudella; tällaiset kokeet ovat osoittaneet, että minkä tahansa kappaleen ns. painava massa on hyvin tarkasti sama kuin ns. hidas massa.^[44] Lisää historiallista tietoa gravitaatiovarjostuksen ja Le Sagen gravitaatioteorian välillä, katso ^[45][46] ja Borzeszkowski ym..^[47]

Koska Isenkrahen ehdotus, jonka mukaan kappaleen tiheys, lämpötila ja paino liittyisivät toisiinsa, perustui ainoastaan aineen tiheyden oletettuihin muutoksiin ja koska lämpötila voi nousta tai aleta tiheyden muuttumatta, Isenkheren kommentit eivät anna aihetta olettaa mitään perustavaa yhteyttä lämpötilan ja gravitaation välille. (Tosin on kyllä olemassa yhteys lämpötilan ja gravitaation, samoin kuin sidosenergian ja gravitaation välillä, mutta tällä ei ole mitään tekemistä Isenkrahen ehdotuksen kanssa, katso alempaa kohdasta "Gravitaatio ja energia".) Mitkään koetulokset eivät myöskään osoita, että olisi olemassa ehdotuksen mukainen yhteys gravitaation ja tiheyden välillä.

Gravitaation nopeus

Vastus

Le Sagen teorian mukaan jokaiseen kappaleeseen, joka liikkuu suhteessa iso­trooppiseen ultra­mundaaniseen virtaan (siis koordinaatistoon, jonka suhteen ultra­mundaanisten korpuskelien nopeus on kaikkiin suuntiin sama), kohdistuu väliaineen vastus. Tämä johtuu siitä, että jos kappale on liikkeessä, siihen edestä­päin osuvilla hiukkasilla on suurempi suhteellinen nopeus kuin siihen takaa­päin osuvilla. Tämä ilmiö vähitellen myös hidastaisi Maan kierto­liikettä Auringon ympäri. Tämä vastus on verrannollinen tuloon vu, missä u on kappaleen ja v ultra­mundaanisten hiukkasten nopeus, kun taas niiden aiheuttama gravitaatio­vaikutus on verrannollinen hiukkasten nopeuden neliöön v². Näin ollen vastuksen ja gravitaatio­voiman suhde on verrannollinen suhteeseen u/v. Kun gravitaatio­voima on tietyn suuruinen, tietyllä nopeudella u liikkuvaan kappaleeseen kohdistuva vastus voi olla kuinka pieni tahansa, jos ultra­mundaanisten hiukkasten nopeus v on tarpeeksi suuri. Tällaista vastusta ei kuitenkaan ole havaittu, joten sen on oltava erittäin pieni, mikä edellyttää, että hiukkasten nopeuden v on oltava erittäin suuri, jopa useita suuruus­luokkia valon­nopeuttakin suurempi. Tämän vuoksi Le Sagen teoria on ilmeisessä ristiriidassa erityisen suhteellisuus­teorian kanssa, jonka mukaan mikään hiukkanen tai aalto ei voi liikkua valoa nopeammin. Sitä paitsi, vaikka valoa nopeammat hiukkaset olisivatkin mahdollisia, tällaisen virran efektiivinen lämpötila olisi niin korkea, että se tuhoaisi kaiken tavallisen aineen sekunnin murto-osassa.

Häiriöt kiertoliikkeessä

Kuten Laplace osoitti, Le Sagen teoriasta seuraisi epäsäännöllisyyksiä taivaankappaleiden kierto­liikkeessä, koska gravitaatiolla olisi äärellinen nopeus. Elleivät Le Sagen hiukkaset liiku paljon valoa nopeammin, niin kuin Le Sage ja Kelvin otaksuivat, kappaleet vaikuttavat toisiinsa vasta tietyllä viiveellä. Kierto­liikkeen tapauksessa tämä johtaisi siihen, että kukin kappale reagoisi siihen, missä toinen kappale oli tietyllä aikaisemmalla hetkellä, mistä aiheutuisi oma voima­komponenttinsa. Päinvastoin kuin vastus­voimasta, tästä aiheutuisi molemmille kappaleille kiihtyvyyttä toisistaan poispäin. Jotta kierto­radat pysyisivät vakaana, gravitaatio­vaikutuksen on joko edettävä paljon valoa nopeammin tai se ei voi olla keskeisvoima. Monet ovat pitäneet tätä ratkaisevana todisteena Le Sagen teoriaa vastaan. Sitä vastoin yleinen suhteellisuusteoria ei ole risti­riidassa sen kanssa, ettei tällaisia häiriöitä esiinny, sillä vaikka gravitaatio eteneekin valon­nopeudella, vuoro­vaikutuksella on myös nopeudesta riippuvia komponentteja, jotka lähes täsmälleen kumoavat nämä häiriöt.^[48]

Gravitaation kantama

Monissa hiukkasmalleissa kuten Kelvinin esittämässä gravitaation kantama on rajoitettu, koska hiukkaset vuorovaikuttavat myös toistensa kanssa. Tämän kantaman määrittää pääasiassa se, kuinka nopeasti hiukkasten ehdotetut "sisäiset energiatasot" voivat kumota sen nopeuden pienenemisen, joka tapahtuu niiden kulkiessa aineen läpi. Teorian ennustama gravitaation kantama riippuu siitä, millaiseksi nämä vuorovaikutukset oletetaan. Joka tapauksessa tällaisten mallien mukaan on kuitenkin rajoituksia sille, kuinka suuret rakenteet maailmankaikkeudessa voivat gravitaation ansiosta pysyä koossa.

Energia

Absorptio

Kuten edellä teorian historiaa käsittelevässä osiossa on todettu, suuren ongelman Le Sagen teoriassa muodostaa kysymys energiasta ja lämmöstä. Kuten Maxwell ja Poincaré osoittivat, kimmottomat törmäykset kuumentaisivat ainetta niin paljon, että se höyrystyisi sekunnin murto-osassa, eivätkä tälle ongelmalle esitetyt ratkaisut ole vakuuttavia. Esimerkiksi Aronson^[27] esitti Maxwellin väitteelle yksinkertaisen todistuksen:

»Olettakaamme, että vastoin Maxwellin hypoteesia tavallisen aineen molekyyleillä olisi enemmän energiaa kuin hiukkasilla. Siinä tapauksessa hiukkaset keskimäärin saisivat energiaa törmäyksissä, ja kappaleeseen B osuvat hiukkaset olisivat suurienergisempiä poistuessaan kappaleesta B. Silloin gravitaatio vaikuttaisi päinvastoin: kaikkien kappaleiden välillä vaikuttaisi hylkivä voima, mikä vastoin on havaintoja. Jos taas hiukkasten ja molekyylien keskimääräinen liike-energia on sama, nettomääräistä energian siirtoa ei tapahtuisi ja törmäykset olisivat kimmoisia, mikä, kuten on todettu, ei saisi aikaan gravitaation kaltaista voimaa.»

Myöskään Isenkrahen teorian mukaista energian säilymis­lain rikkoutumista ei voida hyväksyä, ja Clausiuksen teoreema Kelvinin soveltamana johtaisi, kuten Kelvin itse totesi, jonkinlaiseen ikiliikkujan kaltaiseen mekanismiin. Aalto­malleihin liittyvä ajatus sekundaarisesta säteilystä, joka kuljettaisi ylimääräisen energian pois, kiinnosti J. J. Thomsonia, mutta Maxwell ja Poincaré eivät ottaneet sitä vakavasti, koska se rikkoisi karkeasti termo­dynamiikan toista pää­sääntöä, joka kuitenkin on yksi fysiikan varmimmin todennetuista laeista: suuri määrä energiaa siirtyisi kylmästä kappaleesta kuumempaan vastoin toista pää­sääntöä.

Energiaongelmaa on käsitelty myös sen ajatuksen yhteydessä, että massa kasvaisi, kuten laajenevan Maan teorioissa oletetaan. Varhaisia teoreetikkoja, jotka yhdistivät massan kasvun jonkinlaisen työntävän gravitaation mallissa Maan laajenemiseen, olivat Yarkovsky ja Hilgenberg.^[49] Ajatusta massan kasvusta ja laajenevan Maan teoriaa eivät nykyiset valta­virran tieteilijät pidä uskottavina. Muiden seikkojen ohella sitä vastaan puhuu massan ja energian ekvivalenssi: jos Maa absorboisi ultra­mundaanisen hiukkas­virran energiaa niin paljon, että tämä ilmiö voisi aiheuttaa havaitun gravitaation, ja jos käytetään Poincarén laskemia arvoja, sen massan pitäisi kaksin­kertaistua sekunnin murto-osassa.

Gravitaation kytkeytyminen energiaan

Havaintojen perusteella tiedetään, että gravitaatio vaikuttaa kaikkiin energian muotoihin, ei ainoastaan massaan. Atomi­ytimen sähköinen sidos­energia, heikon vuoro­vaikutuksen energia ytimen sisällä ja atomin elektronien liike-energia vaikuttavat kaikki atomin painavaan massaan, minkä Eötvösin koe on osoittanut hyvin suurella tarkkuudella.^[50] Tämä merkitsee esimerkiksi, että jos kaasun atomit liikkuvat nopeammin, sen paino kasvaa. Lisäksi laserilla tehdyt mittaukset osoittavat, että gravitaatioon liittyvä sidos­energia itsekin on gravitaation vaikutuksen alainen ja että tämä vaikutus on suurella tarkkuudella ekvivalenssi­peri­aatteen mukainen. Tämäkin osoittaa, että jokaisen onnistuneen gravitaatio­teorian on oltava epä­lineaarinen ja otettava tämä itseensä kytkeytyminen huomioon.^[51][52] Le Sagen teoria tai mikään sen muunnelma ei kuitenkaan ennusta tai selitä mitään näistä edellä mainituista ilmiöistä.

Samantapaisia selityksiä muille ilmiöille

Valegravitaatio

Vuonna 1941 Lyman Spitzer ^[53] laski, että jos kaksi pölyhiukkasta absorboivat säteilyä, tämä saa niiden välille aikaan vetävän voiman, joka on kääntäen verrannollinen niiden etäisyyden neliön. Hän ilmeisesti oli kuitenkin tietämätön Le Sagen teoriasta ja varsinkin Lorentzin säteilypainetta ja gravitaatiota koskevista teorioista. George Gamow, joka nimitti tätä ilmiötä "valegravitaatioksi" (engl. mock gravity), ehdotti vuonna 1949^[54] että alkuräjähdyksen jälkeen elektronien lämpötila aleni nopeammin kuin taustasäteilyn. Säteilyn absorptio olisi saanut elektronien välille aikaan Le Sagen teorian kaltaisia voimia, mikä olisi saattanut huomattavasti vaikuttaa galaksien muodostumiseen pian alkuräjähdyksen jälkeen. Vuonna 1971 Field kuitenkin osoitti tämän hypoteesin vääräksi^[55], sillä vaikutus olisi aivan liian heikko, koska elektronit ja säteily olivat lähes termisessä tasapainossa. Hogan ja White ehdottivat vuonna 1986^[56], että ennen galakseja muodostuneiden tähtien valon absorboituminen ja siitä aiheutuva valegravitaatio olisi voinut vaikuttaa galaksien muodostumiseen. Wang ja Field kuitenkin osoittivat^[57] ettei valegravitaatio missään muodossa voi olla kyllin voimakas voidakseen vaikuttaa galaksien muodostumiseen.

Plasma

Le Sagen teoriaan verrattavalla mekanismilla on suuri merkitys myös plasman käyttäytymisessä. A.M. Ignatov^[58] on osoittanut, että kahden pölyhiukkasen välille muodostuu vetävä voima, jos ne on upotettu isotrooppiseen plasmaan, mikä johtuu kimmottomista törmäyksistä plasman ionien ja pölyhiukkasten välillä. Tämä vetovoima on kääntäen verrannollinen pölyhiukkasten välisen etäisyyden neliöön ja se voi kumota niiden välisen Coulombin lain mukaisen poistovoiman.

Tyhjiöenergia

Kvanttikenttäteorian mukaan on olemassa virtuaalisia hiukkasia, jotka saavat aikaan niin sanotun Casimirin ilmiön. Casimir laski, että kahden tason välillä vain ne hiukkaset, joilla on tietty aallonpituus, on otettava huomioon laskettaessa tyhjiöenergiaa. Sen vuoksi energiatiheys kahden tason välillä on pienempi, jos ne ovat lähellä toisiaan, mikä saa aikaan vetävän voiman niiden välille. Tämän ilmiön käsitteellinen perusta on kuitenkin hyvin toisenlainen kuin Fation ja Le Sagen teorioiden.

Viimeaikaisia käsityksiä

Le Sagen teorian uudelleenkäsittely 1800-luvulla osoitti teoriassa useita toisiinsa läheisesti liittyviä ongelmia. Ne liittyvät suureen kuumenemiseen, hiukkasten aiheuttamaan vastukseen, varjostukseen ja teorian ennustamiin poikkeamiin Newtonin gravitaatiolaista. Näiden ongelmien tunnistaminen sekä yleinen siirtyminen pois mekaniikkaan perustuvista teorioista johtivat siihen, että Le Sagen teoria sai osakseen yhä vähemmän mielenkiintoa. Lopulta 1900-luvulla se jäi kokonaan Einsteinin yleisen suhteellisuusteorian varjoon.

Vuonna 1965 Richard Feynman käsitteli Fation-Le Sagen mekanismia luennoillaan ja niihin perustuvassa teoksessa Fysiikan lain luonne, tosin mainitsematta heidän nimiään, pääasiassa yrityksenä selittää "monimutkainen" fysiikan laki (tässä tapauksessa Newtonin laki, jonka mukaan gravitaatio on kääntäen verrannollinen etäisyyden neliöön) yksinkertaisempien ilmiöiden avulla ilman moni­mutkaista matematiikkaa, mutta samalla myös esimerkkinä epä­onnistu­neesta teoriasta. Hän huomautti, että "kimpoavien kappaleiden" mekanismi saisi aikaan tämän verrannollisuuden ja että "matemaattisen suhteen omituisuus vähenee täten hyvin paljon", mutta toteaa sitten, että teoria "ei toimi" sen vastuksen vuoksi, jonka eteneviin kappaleisiin pitäisi sen mukaan kohdistua, minkä vuoksi teoria on hylättävä.^[59][60]

Vaikka valtavirran tiedeyhteisö ei pidä teoriaa uskottavana, valtavirran ulkopuolella ilmaantuu toisinaan yhä yrityksiä selittää gravitaatio sen mukaisesti. Sellaista teorioita ovat yrittäneet luoda esimerkiksi Radzievskii ja Kagalnikova (1960),^[61] Shneiderov (1961),^[62] Buonomano ja Engels (1976),^[63] Adamut (1982),^[64] Jaakkola (1996),^[65], Tom Van Flandern (1999),^[66] ja Edwards (2007)^[67]

Äskettäinen työpaperi uudesta kvantitatiivisesta painovoiman teoriasta, jota ei ole vielä vertaisarvioitu, on ilmestynyt CERN Zenodo -alustalle ^[68].

Lähteet

• Aronson, S.: The gravitational theory of Georges-Louis Le Sage. The Natural Philosopher, 1964, nro 3, s. 51–74. Artikkelin verkkoversio. (Arkistoitu – Internet Archive)
• Bellone, E.: Classic and non-intentional consequences of some newtonian problems. Mem. Società Astronomica Italiana, 1991, 62. vsk, nro 3, s. 477–485. Bibcode:1991MmSAI..62..477B
• Borzeszkowski, H.-H., Chrobok, T., Treder, H.-J.: Screening and absorption of gravitation in pre-relativistic and relativistic theories. Proceedings of the 18th Course of the School on Cosmology and Gravitation, 2004, s. 1–37. arXiv:gr-qc/0310081
• Chabot, H.: Nombre et approximations dans la théorie de la gravitation de Lesage. Actes des Journées de Peirescq "La pensée numérique", Sciences et Techniques en Perspective, 2ème série, 2004, nro 8, s. 179–198. Artikkelin verkkoversio. (PDF) (Arkistoitu – Internet Archive)
• Corry, L.: David Hilbert between Mechanical and Electromagnetic Reductionism. Archive for History of Exact Sciences, 1999, 53. vsk, nro 6, s. 489–527. Artikkelin verkkoversio. (PDF)^{[vanhentunut linkki]}
• Drude, Paul: Ueber Fernewirkungen. Annalen der Physik, 1897, 12. vsk, nro 298, s. I–XLIX. doi:10.1002/andp.18972981220 Bibcode:1897AnP...298D...1D
• Evans, J. C.: Pushing Gravity: New Perspectives on Le Sage’s Theory of Gravitation, s. 9–40. (Artikkeli ”Gravity in the century of light: sources, construction and reception of Le Sage’s theory of gravitation”) C. Roy Keys Inc., 2002.
• Martins, de Andrade, R.: The Expanding Worlds of General Relativity (Einstein Studies), s. 3–44. (The search for gravitational absorption in the early 20th century by Goemmer, H. & Renn, J. & Ritter, J.) nro 7 Boston: Birkhäuser, 1999. Teoksen verkkoversio.
• Martins, de Andrade, R.: Pushing Gravity: New Perspectives on Le Sage's Theory of Gravitation, s. 239–258, artikkeli "Gravitational absorption according to the hypotheses of Le Sage and Majorana". Montreal: C. Roy Keys Inc., 2002. Teoksen verkkoversio (PDF). (Arkistoitu – Internet Archive)
• Playfair, J.: Notice de la Vie et des Ecrits de George Louis Le Sage (English). Edinburgh Review, 1807, s. 137–153. English summary of Prévost (1805).
• Pierre Prévost: Notice de la Vie et des Ecrits de George Louis Le Sage. Geneve, Pariisi: J.J. Paschoud, 1805. Teoksen verkkoversio.
• Rowlinson, J. S.: Le Sage's Essai de Chymie Méchanique. Notes Rec. R. Soc. London, 2003, 57. vsk, nro 1, s. 35–45. doi:10.1098/rsnr.2003.0195 Artikkelin verkkoversio.^{[vanhentunut linkki]}
• Taylor, W. B.: Kinetic Theories of Gravitation. Annual report of the Smithsonian institution, 1876, nro 31, s. 205–282.
• Wolf, R.: George-Louis Le Sage. Biographien zur Kulturgeschichte der Schweiz, 1862, nro 4, s. 173–192. Orell, Füssli & co.. Artikkelin verkkoversio.
• Zehe, H.: Die Gravitationstheorie des Nicolas Fatio de Duillier. Hildesheim: Gerstenberg, 1980. ISBN 3-8067-0862-2
• Zenneck, J.: Gravitation. Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen, 1903, 5. vsk, nro 1, s. 25–67. Leipzig. Artikkelin verkkoversio. (Arkistoitu – Internet Archive)

Viitteet

1. Fatio de Duillier, N.: Oeuvres complètes de Christiaan Huygens. Société Hollandaise des Sciences, 1888-1950 (1690), nro 9, s. 381–389. The Hague. Artikkelin verkkoversio.
2. Katso sekundaarilähteet, Prévost (1805)
3. Fatio de Duillier, N.: De la Cause de la Pesanteur, Die wiederaufgefundene Abhandlung von Fatio de Duillier: De la cause de la Pesanteur, Drei Untersuchungen zur Geschichte der Mathematik. Schriften der Straßburger Wissenschaftlichen Gesellschaft in Heidelberg, 1929 (1701), nro 10, s. 19–66. Berlin & Leipzig.
4. Fatio de Duillier, N.; Bernard Gagnebin: De la Cause de la Pesanteur: Mémoire de Nicolas Fatio de Duillier. Notes and Records of the Royal Society of London, 1949 (1743), 6. vsk, nro 2, s. 125–160. doi:10.1098/rsnr.1949.0018 Artikkelin verkkoversio.^{[vanhentunut linkki]}
5. H. Zehe: Die Gravitationstheorie des Nicolas Fatio de Duillier. Hildesheim, Gerdesberg, 1980.
6. Cramer, G.: Theses Physico-Mathematicae de Gravitate (väitöskirja). Geneve. Määritä julkaisija!
7. Redeker, F. A.: De cause gravitatis meditatio. Lemgoviae ex officina Meyeriana, 1736.
8. Le Sage, G.-L.: Letter à une académicien de Dijon.. Mercure de France, 1756, s. 153–171.
9. Le Sage, G.-L.: Essai de Chymie Méchanique. omakustanne, 1761. Teoksen verkkoversio.
10. Le Sage, G.-L.: Lucrèce Newtonien. Memoires de l’Academie Royale des Sciences et Belles Lettres de Berlin, 1784, s. 404–432. Artikkelin verkkoversio. (Arkistoitu – Internet Archive)
11. G. L. Le Sage, Pierre Prévost: Deux Traites de Physique Mécanique, s. luku Physique Mécanique des Georges-Louis Le Sage, s. 1–186. Geneve ja Pariisi: J.J. Paschoud, 1818. Teoksen verkkoversio.
12. Wolf (1852), sekundaarilähde
13. Evanes (2002), sekundaarilähde
14. Playfair (1807), sekundaarilähde
15. Lichtenberg, G. C. (muokannut H. Zehe ja W. Hinrichs): Aufzeichnungen über die Theorie der Schwere von G.L. Le Sage. Nachrichten der Akademie der Wissenschaften zu Göttingen, II. Mathematisch-physikalische Klasse, 2003, nro 1.
16. Lichtenberg, saksaksi: "Ist es ein Traum, so ist es der größte und erhabenste der je ist geträumt worden, und womit wir eine Lücke in unseren Büchern ausfüllen können, die nur durch einen Traum ausgefüllt werden kann".
17. Immanuel Kant: Metaphysische Anfangsgründe der Naturwissenschaft, s. Dynamik, Lehrsatz 5. Määritä julkaisija! Teoksen verkkoversio.
18. Friedrich Wilhelm Joseph Schelling: Ideen zu einer Philosophie der Natur (2. kirja, 3. luku). Määritä julkaisija! Teoksen verkkoversio.
19. Pierre-Simon Laplace: A Treatise in Celestial Mechanics. nro 4, kirja 10, luku 7 Chelsea – New York. Määritä julkaisija!
20. Leray, P.: Theorie nouvelle de la gravitation. Comptes Rendus, 1869, nro 69, s. 615–621. Artikkelin verkkoversio.
21. Thomson, William (Lord Kelvin): On the ultramundane corpuscles of Le Sage. Phil. Mag., 1873, nro 45, s. 321–332. Artikkelin verkkoversio.
22. Peter Guthrie Tait: Lectures on some recent advances in physical science with a special lecture on force. Lontoo: Macmillan and Co., 1876. Teoksen verkkoversio.
23. Kelvin, Popular Lectures, vol. i. p. 145.
24. Preston, S. T.: On some dynamical conditions applicable to LeSage’s theory of gravitation. Phil. Mag., fifth ser., 1877, nro 4, s. 206–213 (pt. 1) ja 364–375 (pt. 2).
25. Drude (1897), sekundaarilähde
26. Encyclopædia Britannica, 9. painos, s. 38–47. (hakusana Atom) Määritä julkaisija!
27. Aronson (1960), sekundaarilähde
28. Caspar Isenkrahe: Das Räthsel von der Schwerkraft: Kritik der bisherigen Lösungen des Gravitationsproblems und Versuch einer neuen auf rein mechanischer Grundlage. Braunschweig: Friedrich Vieweg und Sohn, 1879.
29. Ryšánek, A.: Repert. Exp. Phys., 1887, nro 24, s. 90–115.
30. du Bois-Reymond, P.: Ueber die Unbegreiflichkeit der Fernkraft. Naturwissenschaftliche Rundschau, 1888, 3. vsk, nro 14, s. 169–176. Artikkelin verkkoversio.
31. F. A. E ja Ém. Keller: Mémoire sur la cause de la pesanteur et des effets attribués à l'attraction universelle. Comptes Rendus, 1863, nro 56, s. 530–533. Artikkelin verkkoversio.
32. de Boisbaudran, L.: Note sur la théorie de la pesanteur. Comptes Rendus, 1869, nro 69, s. 703–705. Artikkelin verkkoversio.
33. Lorentz, H. A.: Considerations on Gravitation. Proc. Acad. Amsterdam, 1900, nro 2, s. 559–574. Artikkelin verkkoversio.
34. Lectures On Theoretical Physics. Lontoo: Macmillan and Co., 1922, englanninkielinen käännös 1927. Teoksen verkkoversio.
35. Corry (1999), sekundaarilähde
36. J. J. Thomson: Electricity and matter. Westminster: Archibald Constable & Co., Ltd., 1904. Teoksen verkkoversio.
37. J. J. Thomson,: Encyclopædia Britannica, 11. painos, s. 891-895, art. Matter. Määritä julkaisija!
38. Tommasina, T.: La Physique de la Gravitation. Pariisi: Gauthier-Villars, 1928.
39. Brush, C. F.: A kinetic theory of gravitation. Nature, 1911, 86. vsk, nro 2160, s. 130–132. doi:10.1038/086130a0 Bibcode:1911Natur..86..130.
40. Darwin, G. H.: The analogy between Lesage’s theory of gravitation and the repulsion of light. Proc. Royal Soc., 1905, 76. vsk, nro 511, s. 387–410. doi:10.1098/rspa.1905.0042 Bibcode:1905RSPSA..76..387D Artikkelin verkkoversio.
41. George H. Darwin: Introduction to Dynamical Astronomy. Määritä julkaisija!
42. Henri Poincaré: The foundations of science (Science and Method), s. 517–522, kappale "The Theory of LeSage". New York: Science Press.
43. Richard Feynman: Feynman Lectures on Gravitation, s. 23–28. Addison-Wesley, 1995.
44. Lasers, Clocks, and Drag-Free: Technologies for Future Exploration in Space and Tests of Gravity, 2006, s. 27–67. H. Dittus, C. Laemmerzahl, S. Turyshev. arXiv:gr-qc/0602016
45. Martin (1999), sekundaarilähde
46. Martins (2002), sekundaarilähde
47. Borzeskkowski et al. (2004), sekundaarilähde
48. Carlip, S.: Aberration and the Speed of Gravity. Phys. Lett. A, 1999, nro 267, s. 81–87. doi:10.1016/S0375-9601(00)00101-8 Bibcode:2000PhLA..267...81C arXiv:gr-qc/9909087
49. G. Scalera, K.-H. Scalera: Why expanding Earth? – A book in honour of O.C. Hilgenberg. Rooma: INGV, 2003.
50. S. Carlip: Kinetic Energy and the Equivalence Principle. Am. J. Phys., 1997, nro 65, s. 409–413. doi:10.1119/1.18885 Bibcode:1998AmJPh..66..409C arXiv:gr-qc/9909014
51. Eötvös experiments, lunar ranging and the strong equivalence principle. Nature, 20.9.1990, 347. vsk, nro 6290, s. 261–263. doi:10.1038/347261a0 Bibcode:1990Natur.347..261A Artikkelin verkkoversio.
52. Relativity parameters determined from lunar laser ranging. Phys. Rev. D, 1996, 53. vsk, nro 12, s. 6730–6739. doi:10.1103/PhysRevD.53.6730 Bibcode:1996PhRvD..53.6730W Artikkelin verkkoversio. (Arkistoitu – Internet Archive)
53. The dynamics of the interstellar medium; II. Radiation pressure. The Astrophysical Journal, 1941, nro 94, s. 232–244. doi:10.1086/144328 Bibcode:1941ApJ....94..232S
54. On relativistic cosmogony. Reviews of modern physics, 1949, 21. vsk, nro 3, s. 367–373. doi:10.1103/RevModPhys.21.367 Bibcode:1949RvMP...21..367G
55. Field, G. B.: Instability and waves driven by radiation in interstellar space and in cosmological models. The Astrophysical Journal, 1971, nro 165, s. 29–40. doi:10.1086/150873 Bibcode:1971ApJ...165...29F
56. Hogan, C.J.: Mock gravity and cosmic structure. The Astrophysical Journal, 1989, nro 340, s. 1–10. doi:10.1086/167371 Bibcode:1989ApJ...340....1H
57. B. Wang, G.B. Field,: Galaxy formation by mock gravity with dust? The Astrophysical Journal, 1989, nro 346, s. 3–11. doi:10.1086/167981 Bibcode:1989ApJ...346....3W
58. Ignatov, A.M.: Lesage gravity in dusty plasma. Plasma Physics Reports, 1996, 22. vsk, nro 7, s. 585–589. Bibcode:1996PlPhR..22..585I
59. Richard Feynman: Fysiikan lain luonne (The Character of Physical Law), s. 29–31. Suomentanut Kimmo Pietiläinen. Ursa, 1999 (alkuteos 1965). ISBN 952-5329-02-X
60. video Feynmanin esitys aiheesta 7 minuutissa youtube.com. Viitattu 22.5.2012.
61. The nature of gravitation. Vsesoyuz. Astronom.-Geodezich. Obsch. Byull., 1960, 26. vsk, nro 33, s. 3–14.
62. On the internal temperature of the earth. Bollettino di Geofisica Teorica ed Applicata, 1961, nro 3, s. 137–159.
63. Some speculations on a causal unification of relativity, gravitation, and quantum mechanics. Int. J. Theor. Phys., 1976, 15. vsk, nro 3, s. 231–246. doi:10.1007/BF01807095 Bibcode:1976IJTP...15..231B
64. The screen effect of the earth in the TETG. Theory of a screening experiment of a sample body at the equator using the earth as a screen. Nuovo Cimento C, 1982, 5. vsk, nro 2, s. 189–208. doi:10.1007/BF02509010 Bibcode:1982NCimC...5..189A
65. Action-at-a-distance and local action in gravitation: discussion and possible solution of the dilemma. Apeiron, 1996, 3. vsk, nro 3-4, s. 61–75. Artikkelin verkkoversio. (PDF)^{[vanhentunut linkki]}
66. Dark Matter, Missing Planets and New Comets, s. Chapters 2–4. 2 painos. Berkeley: North Atlantic Books, 1999.
67. Edwards, M .R.: Photon-Graviton Recycling as Cause of Gravitation. Apeiron, 2007, 14. vsk, nro 214–233. Artikkelin verkkoversio. (PDF)^{[vanhentunut linkki]}
68. Novel quantitative push gravity theory poised for verification. Zenodo, 2020. doi:10.5281/zenodo.4284106 Artikkelin verkkoversio.

Aiheesta muualla

• Mathpage: LeSage's Shadows, Omni-Directional Flux, Kinetic Pressure and Tetrode’s Star, Nicolas Fatio and the Cause of Gravity^{[vanhentunut linkki]}, Fatio, Le Sage and the camisards^{[vanhentunut linkki]}, Historical Assessments of the Fatio-Lesage Theory^{[vanhentunut linkki]}

Ei valtavirran

• Halton Arp: The Observational Impetus for Le Sage Gravity
• Auffray, J.-P.: Preston on E=mc² and Dual origin of E=mc²
• Borg Xavier : Electromagnetic radiation pressure (EMRP) gravity theory – Blaze Labs Research
• Buonomano, V.: Co-Operative Phenomena as a Physical Paradigm for Special Relativity, Gravitation and Quantum Mechanics
• Edwards, et al.: Pushing Gravity (Arkistoitu – Internet Archive)
• Mingst, B. & Stowe, P.: Derivation of Newtonian Gravitation from LeSage's Attenuation
• Popescu, I.I.: Ether and Etherons
• Tom Van Flandern: Possible new properties of gravity (Arkistoitu – Internet Archive)
• A. Acke: Theoretical foundation of gravito-electromagnetism. prespacetime.com. 2010.

Käännös suomeksi

Tämä artikkeli tai sen osa on käännetty tai siihen on haettu tietoja muunkielisen Wikipedian artikkelista.
Alkuperäinen artikkeli: en:Le Sage's theory of gravitation