Équation de Sackur-Tetrode
L'équation de Sackur-Tetrode, établie en 1912[1] par les physiciens Otto Sackur[2] et Hugo Tetrode[3],[4], donne l'entropie d'un gaz parfait monoatomique, non dégénéré, non relativiste.
Soit la longueur d'onde thermique de de Broglie : , et le volume correspondant.
Alors, l'entropie S = S(U,V,N) du gaz (défini par son volume V, son énergie interne U et son nombre de particules N) vaut :
soit en développant :
- .
Les expressions ci-dessus supposent que le gaz est dans le régime classique et est décrit par la statistique de Maxwell-Boltzmann (avec le "décompte correct de Boltzmann"). D'après la définition de la longueur d'onde thermique, cela signifie que l'équation de Sackur-Tetrode est valable uniquement quand :
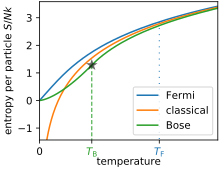
L'entropie prédite par l'équation de Sackur-Tetrode tend vers moins l'infini quand la température tend vers zéro.
En chimie, on préfère parfois retenir plutôt l'enthalpie libre G = U + NkT -TS = -NkT. Ln P/P(T) avec P(T) = kT/Vo :
G =-RT.LnP + cste(T) est le fondement de la loi d'action de masse :
on obtient ainsi les ordres de grandeur des constantes d'équilibre Kp(T) des réactions.
Constante de Sackur-Tetrode
[modifier | modifier le code]La constante de Sackur–Tetrode, écrite S0/R, est égale à S/kBN évaluée à la température de T = 1 kelvin, à la pression standard (100 kPa ou 101,325 kPa, à préciser), pour une mole d'un gaz idéal composé de particules de masse égale à l'unité de masse atomique unifiée (mu = 1,66053906660(50)×10−27 kg). Sa valeur recommandée par CODATA 2018 est :
- S0/R = −1,151 707 537 06 ± (45) pour p
o= 100 kPa[5] - S0/R = −1,164 870 523 58 ± (45) pour p
o= 101,325 kPa[6].
Gaz rares
[modifier | modifier le code]En chimie, on donne l'entropie molaire standard dans les conditions standard (25 °C, P = 1 × 105 Pa).
Le calcul pour m = 40 u donne 154,8 J/K/mol
Les valeurs de l'entropie molaire standard S° (en J K-1 mol-1) données par CODATA sont :
- Hélium : M = 4,002602 u - S° = 126,153(2) ;
- Néon : M = 20,1797 u - S° = 146,328(3) ;
- Argon : M = 39,948 u - S° = 154,846(3) ;
- Krypton : M = 83,80 u - S° = 164,085(3) ;
- Xénon : M = 131,29 u - S° = 169,685(3) ;
- Radon : M = 222 u - S° = 176,23.
On pourra vérifier que les données s'accordent pour donner : S° = S°(M=1) +3/2 R.Ln M
avec une assez bonne corrélation à condition de modifier légèrement pour l'hélium la correction de de Boer ; S°(M=1) est même négative, ce qui laisse parfois perplexes certains[Quoi ?], inattentifs à la condition de non-dégénérescence.
En comptant en bit[Quoi ?]/molécule, on retient que pour l'Argon, S° =~ 27 bits/molécule pour M = 40 : évidemment il faut S° assez grand, sinon la dégénérescence quantique doit être évaluée.
Références
[modifier | modifier le code]- ↑ (en) Walter Grimus, « 100th anniversary of the Sackur–Tetrode equation », Annalen der Physik, vol. 525, no 3, , A32–A35 (ISSN 0003-3804, DOI 10.1002/andp.201300720
 , Bibcode 2013AnP...525A..32G, arXiv 1112.3748)
, Bibcode 2013AnP...525A..32G, arXiv 1112.3748)
- ↑ Sackur publia ses découvertes dans la série suivante d'articles :
- (de) O. Sackur, « "Die Anwendung der kinetischen Theorie der Gase auf chemische Probleme" » [« The application of the kinetic theory of gases to chemical problems »], Annalen der Physik, vol. 36, , p. 958–980.
- O. Sackur, "Die Bedeutung des elementaren Wirkungsquantums für die Gastheorie und die Berechnung der chemischen Konstanten" (The significance of the elementary quantum of action to gas theory and the calculation of the chemical constant), Festschrift W. Nernst zu seinem 25jährigen Doktorjubiläum gewidmet von seinen Schülern (Halle an der Saale, Germany: Wilhelm Knapp, 1912), pages 405–423.
- (de) O. Sackur, « "Die universelle Bedeutung des sog. elementaren Wirkungsquantums" » [« The universal significance of the so-called elementary quantum of action »], Annalen der Physik, vol. 40, , p. 67–86
- ↑ (de) H. Tetrode, « "Die chemische Konstante der Gase und das elementare Wirkungsquantum" » [« The chemical constant of gases and the elementary quantum of action »], Annalen der Physik, vol. 38, , p. 434–442
- ↑ (de) H. Tetrode, « Berichtigung zu meiner Arbeit: "Die chemische Konstante der Gase und das elementare Wirkungsquantum" » [« Correction to my work: "The chemical constant of gases and the elementary quantum of action" »], Annalen der Physik, vol. 39, , p. 255–256 (lire en ligne)
- ↑ (en) « 2018 CODATA Value: Sackur–Tetrode constant », The NIST Reference on Constants, Units, and Uncertainty, NIST, (consulté le )
- ↑ (en) « 2018 CODATA Value: Sackur–Tetrode constant », The NIST Reference on Constants, Units, and Uncertainty, NIST, (consulté le )
Voir aussi
[modifier | modifier le code]- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Sackur–Tetrode equation » (voir la liste des auteurs).



![{\displaystyle {\frac {S}{kN}}=\ln \left[{\frac {V}{N\Lambda ^{3}}}\right]+{\frac {5}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f1cd15c69b66a8ae6f497fc7144105c0b542137)
![{\displaystyle S=kN\ln \left[\left({\frac {V}{N}}\right)\left({\frac {U}{N}}\right)^{\frac {3}{2}}\right]+{\frac {3}{2}}kN\left({\frac {5}{3}}+\ln {\frac {4\pi m}{3h^{2}}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43877d5ad3b5b697818e920f9ce8473ea6b5857a)
