Algorithme t-SNE
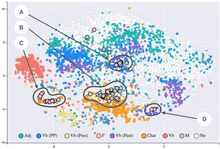
L'algorithme t-SNE (t-distributed stochastic neighbor embedding) est une technique de réduction de dimension pour la visualisation de données développée par Geoffrey Hinton et Laurens van der Maaten et publiée en 2008[1].
Il s'agit d'une méthode non linéaire permettant de représenter un ensemble de points d'un espace à grande dimension dans un espace de deux ou trois dimensions. Les données peuvent ensuite être visualisées sous la forme d'un nuage de points. L'algorithme t-SNE tente de trouver une configuration optimale selon un critère de théorie de l'information afin de conserver la proximité entre les points pendant la transformation : deux points qui sont proches (resp. éloignés) dans l'espace d'origine doivent être proches (resp. éloignés) dans l'espace de faible dimension.
Description
[modifier | modifier le code]L'algorithme t-SNE se base sur une interprétation probabiliste des proximités. Une distribution de probabilité est définie sur les paires de points de l'espace d'origine de telle sorte que des points proches l'un de l'autre ont une forte probabilité d'être choisis tandis que des points éloignés ont une faible probabilité d'être sélectionnés. Une distribution de probabilité est également définie de la même manière pour l'espace de visualisation. L'algorithme t-SNE consiste à faire concorder les deux densités de probabilité, en minimisant la divergence de Kullback-Leibler entre les deux distributions par rapport à l'emplacement des points sur la carte.
L'algorithme t-SNE a été utilisée pour de nombreuses applications : analyse de la musique[2], recherche sur le cancer[3], bioinformatique[4], et le traitement de signaux biomédicaux[5]. Cette méthode est souvent utilisée pour la visualisation de représentations de haut-niveau apprises par un réseau de neurones artificiel[6].
Références
[modifier | modifier le code]- L.J.P. van der Maaten et Hinton, G.E., « Visualizing High-Dimensional Data Using t-SNE », Journal of Machine Learning Research, vol. 9, , p. 2579–2605 (lire en ligne)
- (en) P. Hamel et Eck, D., « Learning Features from Music Audio with Deep Belief Networks », Proceedings of the International Society for Music Information Retrieval Conference, , p. 339–344
- (en) A.R. Jamieson, Giger, M.L., Drukker, K., Lui, H., Yuan, Y. et Bhooshan, N., « Exploring Nonlinear Feature Space Dimension Reduction and Data Representation in Breast CADx with Laplacian Eigenmaps and t-SNE », Medical Physics, vol. 37, no 1, , p. 339–351 (DOI 10.1118/1.3267037)
- (en) I. Wallach et Liliean, R., « The Protein-Small-Molecule Database, A Non-Redundant Structural Resource for the Analysis of Protein-Ligand Binding », Bioinformatics, vol. 25, no 5, , p. 615–620 (PMID 19153135, DOI 10.1093/bioinformatics/btp035)
- (en) J. Birjandtalab, M. B. Pouyan et M. Nourani, « Nonlinear dimension reduction for EEG-based epileptic seizure detection », 2016 IEEE-EMBS International Conference on Biomedical and Health Informatics (BHI), , p. 595–598 (DOI 10.1109/BHI.2016.7455968, lire en ligne)
- Visualizing Representations: Deep Learning and Human Beings Christopher Olah's blog, 2015