Connexité (mathématiques)

La connexité est une notion de topologie qui formalise le concept d'« objet d'un seul tenant ». Un objet est dit connexe s'il est fait d'un seul « morceau ». Dans le cas contraire, chacun des morceaux est une composante connexe de l'objet étudié.

Un archipel, comme celui des îles Canaries, n'est pas connexe : il n'est pas possible de passer à pied sec d'une île à l'autre. Les îles sont les composantes connexes de l'archipel.

Définition

L'espace vert A est connexe, alors que l'espace bleu B ne l'est pas.

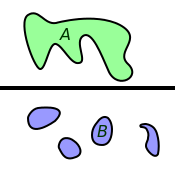
Soit un espace topologique E. Les quatre propositions suivantes sont équivalentes :

• E n'est pas la réunion de deux ouverts non vides disjoints ;
• E n'est pas la réunion de deux fermés non vides disjoints ;
• les seuls ouverts-fermés de E sont ∅ et E ;
• toute application continue de E dans un ensemble à deux éléments muni de la topologie discrète est constante.

Dans le cas où l'une de ces conditions équivalentes est remplie, on dit que l'espace E est connexe.

La dernière de ces quatre caractérisations est souvent la plus commode à utiliser pour démontrer un résultat de connexité.

Une partie X d'un espace topologique E est dite connexe si elle est un espace connexe lorsqu'elle est munie de la topologie induite.

Connexité et nombres réels

Les parties connexes de ℝ sont les intervalles^[1].

Propriétés

Exemples d'unions et d'intersections connexes ou non.

• La notion de connexité est clairement invariante par homéomorphismes.
• Tout ensemble muni de sa topologie grossière est connexe. Il en résulte que l'ensemble vide est connexe, ainsi que tout espace réduit à un point.

Union, intersection, adhérence, produit

Si X et Y sont deux parties connexes d'un espace topologique, en général l'union et l'intersection de X et Y ne sont pas connexes^[2].

En revanche, l'union des deux parties connexes est connexe dès qu'elles ont un point commun (il suffit même que l'une des deux rencontre l'adhérence de l'autre). Plus généralement :

• Pour toute famille (finie ou pas) de parties connexes dont l'intersection est non vide, la réunion est connexe.

Exemples d'application :

• toute partie connexe par arcs est connexe (comme réunion des chemins dans cette partie ayant tous une même origine fixée), en revanche la réciproque est fausse^[2];
• si ${\displaystyle (X_{n})_{n\in \mathbb {N} }}$ est une suite de parties connexes telle que chacune a un point commun avec la suivante ${\displaystyle (\forall n\in \mathbb {N} ,X_{n}\cap X_{n+1}\neq \varnothing )}$ alors la réunion ${\displaystyle \cup _{n\in \mathbb {N} }X_{n}}$ est connexe (comme réunion des ${\displaystyle Y_{n}:=\cup _{k\leq n}X_{k}}$ qui, par récurrence, sont connexes).

Si A est une partie connexe de E alors son adhérence A est connexe car plus généralement, toute partie B de E telle que A ⊂ B ⊂ A est connexe.

Théorème du passage à la douane : dans un espace topologique, toute partie connexe qui rencontre à la fois une partie C et son complémentaire rencontre nécessairement la frontière de C^[1].

Un produit d'espaces non vides est connexe si (et seulement si) chaque facteur l'est. Plus généralement, l'espace total d'un fibré de base et de fibre connexes est connexe^[3].

Composantes connexes

Étant donné un point x d'un espace topologique E, la réunion de toutes les parties connexes contenant x est connexe. C'est la plus grande (au sens de la relation d'inclusion) de toutes les parties connexes contenant x. On la note C_x et on l'appelle composante connexe de x dans E. Les composantes connexes des points de E sont donc les parties connexes maximales pour l'inclusion (il n'y en a qu'une si l'espace est connexe). Elles forment une partition de E ; autrement dit : ce sont les classes d'une relation d'équivalence sur E. Deux points de E sont dits connectés s'ils sont dans la même composante connexe.

Au minimum, on a C_x = {x} ; cela signifie que {x} est le seul sous-ensemble connexe de E contenant x mais pas forcément que x est un point isolé (voir exemples). Si C_x = {x} pour tout point x de E, on dit que E est totalement discontinu. Au maximum, on a C_x = E ; c'est le cas où E est connexe.

Les composantes connexes sont toujours fermées mais pas toujours ouvertes (elles le sont si et seulement si l'espace est leur somme topologique) ; cependant :

• les composantes connexes d'un espace localement connexe sont ouvertes ;
• toute partie connexe non vide qui est à la fois fermée et ouverte est une composante connexe.

Exemples

• ℝ* a deux composantes connexes : ℝ₊* et ℝ_–*.
• Plus généralement, le groupe GL(n, ℝ) des matrices inversibles de taille n a deux composantes connexes, données par le signe du déterminant.
• Dans ℕ et plus généralement dans un espace muni de la topologie discrète, les composantes connexes sont les singletons.
• Dans ℚ, aucun point n'est isolé, mais les composantes connexes sont aussi les singletons. Le même phénomène se produit pour l'ensemble de Cantor. Ce sont donc des exemples d'espaces totalement discontinus.
• Tout ouvert de ℝ est localement connexe (car ℝ l'est) donc est réunion (donc réunion au plus dénombrable) ∪_k∈κI_k d'intervalles ouverts non vides disjoints : ses composantes connexes. Il est donc homéomorphe à ℝ×κ (où κ est muni de la topologie discrète).

Connexité et continuité

D'après la définition, un espace est connexe lorsque son image par une application continue n'est jamais l'espace discret {0, 1}. Or ce dernier est (a fortiori) non connexe. Plus généralement :

Toute image continue d'un connexe est connexe.

C'est-à-dire que si E est un espace connexe et f une application continue de E dans un espace F, alors f(E) est une partie connexe de F. En effet, si g est une application continue de f(E) dans l'espace discret {0, 1}, alors g∘f — continue sur le connexe E — est constante donc g est constante. En particulier :

• ceci fournit une preuve du fait que tout chemin est connexe — qui correspond au cas où E est un intervalle réel — et du théorème des valeurs intermédiaires (qui est le cas particulier d'un chemin dans ℝ) à condition d'avoir démontré au préalable que tout intervalle réel est connexe, comme indiqué ci-dessus, sans utiliser ce théorème ;
• tout quotient d'un connexe est connexe.

Applications localement constantes

Définition — Une application f d'un espace topologique X dans un ensemble Y est dite localement constante (en) sur X si tout point de X possède un voisinage sur lequel f est constante.

Une fonction localement constante sur X n'est pas forcément constante sur X, mais c'est le cas si l'espace X est connexe, comme le montre le théorème suivant.

Théorème^[4] — Si f est localement constante sur X alors elle est constante sur chaque composante connexe de X.

La réciproque de ce théorème est fausse en général (prendre X = ℚ), mais vraie si X est localement connexe.

Deux applications fondamentales à l'analyse

Pour montrer qu'une propriété est vraie pour tous les points d'une partie que l'on sait connexe, on montre que l'ensemble des points qui la satisfait est ouvert et fermé.

C'est ce qu'on fait pour le théorème d'unicité des solutions globales d'une équation différentielle, et pour le principe du prolongement analytique.

Applications à la topologie

Les applications sont nombreuses. La droite ℝ et le plan ℝ² ne sont pas homéomorphes : si tel était le cas, la droite privée d'un point serait homéomorphe au plan privé d'un point. Mais le second espace est connexe, le premier ne l'est pas.

Le même argument montre que le cercle S¹ n'est pas homéomorphe à un intervalle.

Cet argument ne s'étend pas aux dimensions supérieures. Si on veut montrer en utilisant les mêmes idées que ℝ² et ℝ³ ne sont pas homéomorphes, il faut faire intervenir la connexité simple (c'est-à-dire la connexité par arcs de l'espace des lacets). Le résultat est encore vrai pour les dimensions supérieures, mais fait appel pour la démonstration à des outils plus puissants comme l'homologie.

On peut encore citer, comme application de la connexité, l'analyse de l'énigme des trois maisons. L'objet de cette énigme est de relier trois points du plan identifiés à des maisons à trois autres, identifiés à des fournisseurs (eau, gaz et électricité). Chaque maison doit être reliée aux trois fournisseurs et les liens ne doivent pas se croiser. La démonstration de l'impossibilité de résolution se fonde sur le théorème de Jordan, qui s'exprime en termes de connexité.

Cas des groupes topologiques

Dans un groupe topologique G, la composante connexe de l'identité, appelée composante neutre (en) et notée G₀, est un sous-groupe distingué. Comme toute composante connexe, G₀ est fermé dans G, et de plus ouvert si G est localement connexe (en particulier si G est localement connexe par arcs, notamment si G est un groupe de Lie). Le groupe quotient G/G₀ (muni de la topologie quotient) est totalement discontinu ; il est discret si et seulement si G₀ est ouvert.

La propriété suivante est très utile pour montrer des résultats de connexité :

Soit G un groupe topologique et H un sous-groupe. Si le groupe H et l'espace G/H sont connexes, alors G est lui-même connexe^[5],[6].

Aussi, si G est un groupe topologique et H un sous-groupe distingué connexe, alors le produit semi-direct de H par l'espace quotient G/H, avec pour action celle induite par le produit dans G, est connexe. On peut ainsi montrer que, si G est un groupe de Lie et H son sous-groupe distingué maximal connexe, alors le produit semi-direct de H par l'espace quotient G/H, muni de la topologie induite à partir d'une décomposition en orbites du fibré normal associé à cette action, est un groupe localement connexe^[7].

Notes et références

1. Cette propriété est démontrée dans le chapitre de Wikiversité sur la connexité (voir infra).
2. Bertrand Hauchecorne, Les contre-exemples en mathématiques, Paris, Ellipses, 2007, 2^e éd. (1^re éd. 1988), 365 p. (ISBN 978-2-7298-3418-0), chap. 15 (« Topologie générale »), p. 300.
3. (en) Gregory Naber, Topology, Geometry, and Gauge Fields: Foundations, Springer, 2013 (lire en ligne), p. 81.
4. Voir par exemple cet exercice corrigé sur Wikiversité.
5. (en) Markus Stroppel, Locally Compact Groups, EMS, 2006 (lire en ligne), p. 55.
6. (en) O. Ya. Viro, O. A. Ivanov, N. Yu. Netsvetaev et V. M. Kharlamov, Elementary Topology, AMS, 2008 (lire en ligne), p. 192 et 201.
7. (en) Charles Nash, Sidney C. Blau et Matthias Blau, Topology and Geometry for Physicists, 1991.

Voir aussi

Sur les autres projets Wikimedia :

• Connexité (mathématiques), sur Wikiversity

Articles connexes

• Espace bien enchaîné
• Espace unicohérent
• Théorème de Phragmén-Brouwer

Bibliographie

• Georges Skandalis, Topologie et analyse 3^e année, Dunod, coll. « Sciences Sup », 2001
• Claude Wagschal, Topologie et analyse fonctionnelle, Hermann, coll. « Méthodes », 1995

• Portail des mathématiques