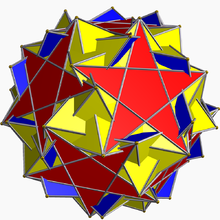
Dodécadodécaèdre adouci inversé
Cet article est une ébauche concernant la géométrie.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
Dodécadodécaèdre adouci inversé
| Faces | Arêtes | Sommets |
|---|---|---|
| 84 (60{3}+12{5}+12{5/2}) | 150 | 60 |
| Type | Polyèdre uniforme |
|---|---|
| Références d'indexation | U60 – C76 – W114 |
| Symbole de Wythoff | | 5⁄3 2 5 |
| Caractéristique | -6 |
| Groupe de symétrie | I |
| Dual | Hexacontaèdre pentagonal médial inversé |
En géométrie, le dodécadodécaèdre adouci inversé est un polyèdre uniforme non convexe, indexé sous le nom U60.
Coordonnées cartésiennes
[modifier | modifier le code]Les coordonnées cartésiennes des sommets d'un dodécadodécaèdre adouci inversé centré à l'origine sont les permutations paires de
- (±2α, ±2, ±2β),
- (±(α+β/τ+τ), ±(-ατ+β+1/τ), ±(α/τ+βτ-1)),
- (±(-α/τ+βτ+1), ±(-α+β/τ-τ), ±(ατ+β-1/τ)),
- (±(-α/τ+βτ-1), ±(α-β/τ-τ), ±(ατ+β+1/τ)) et
- (±(α+β/τ-τ), ±(ατ-β+1/τ), ±(α/τ+βτ+1)),
avec un nombre pair de signes plus, où
- β = (α2/τ+τ)/(ατ−1/τ),
où τ = (1+√5)/2 est le nombre d'or (quelquefois écrit φ) et α est la solution réelle négative de τα4−α³+2α²−α−1/τ, ou approximativement −0,3352090. En prenant les permutations impaires des coordonnées ci-dessus avec un nombre impair de signes plus, cela donne une autre forme, l'énantiomorphe de ce polyèdre.
Voir aussi
[modifier | modifier le code]Lien externe
[modifier | modifier le code]Robert Ferréol, « DODÉCADODÉCAÈDRE ADOUCI INVERSÉ », sur Encyclopédie des formes mathématiques remarquables
