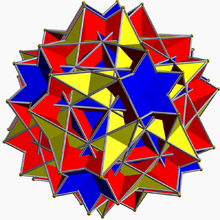
Grand rhombicosidodécaèdre uniforme
Cet article est une ébauche concernant la géométrie.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
Grand rhombicosidodécaèdre uniforme
| Faces | Arêtes | Sommets |
|---|---|---|
| 62 (20{3}+30{4}+12{5/2}) | 120 | 60 |
| Type | Polyèdre uniforme |
|---|---|
| Références d'indexation | U67 – C84 – W105 |
| Symbole de Wythoff | 5⁄3 3 | 2 |
| Caractéristique | 2 |
| Groupe de symétrie | Ih |
| Dual | Grand hexacontaèdre deltoïdal |
En géométrie, le grand rhombicosidodécaèdre est un polyèdre uniforme non-convexe, indexé sous le nom U67. Il est aussi appelé le quasirhombicosidodécaèdre[1].
Ce polyèdre partage son nom avec le grand rhombicosidodécaèdre convexe, qui est aussi appelé l'icosidodécaèdre tronqué. À cause de cette confusion, le mot uniforme a été ajouté au nom de cet article.
Il partage son arrangement de sommet avec le grand dodécaèdre tronqué et avec les composés uniformes de 6 ou 12 prismes pentagonaux.
Coordonnées cartésiennes
[modifier | modifier le code]Les coordonnées cartésiennes pour les sommets d'un rhombidodécadodécaèdre centré à l'origine sont toutes les permutations paires de
- (±1/τ2, 0, ±(2−1/τ))
- (±1, ±1/τ3, ±1)
- (±1/τ, ±1/τ2, ±2/τ)
où τ = (1+√5)/2 est le nombre d'or (quelquefois écrit φ).
Notes et références
[modifier | modifier le code]- ↑ « Grand Battement », Grand Battement, (DOI 10.5040/9781350973695, lire en ligne, consulté le )
