Identité trigonométrique pythagoricienne
L'identité trigonométrique pythagoricienne exprime le théorème de Pythagore en termes de fonctions trigonométriques. Avec les formules de somme d'angles, c'est l'une des relations fondamentales entre les fonctions sinus et cosinus. Cette relation entre le sinus et le cosinus est parfois appelée l'identité trigonométrique fondamentale de Pythagore[1].
Cette identité trigonométrique est donnée par la formule :
- , où signifie .
Si la longueur de l'hypoténuse d'un triangle rectangle est égale à 1, alors la longueur de l'un des deux côtés est le sinus de l'angle opposé et est également le cosinus de l'angle aigu adjacent. Par conséquent, cette identité trigonométrique découle du théorème de Pythagore.
Preuve basée sur les triangles rectangles
[modifier | modifier le code]
Tous les triangles semblables ont la propriété que si nous sélectionnons le même angle dans chacun d'eux, le rapport des deux côtés définissant l'angle est le même quel que soit le triangle similaire choisi, indépendamment de sa taille réelle : les rapports dépendent des trois angles, pas les longueurs des côtés. Ainsi, le rapport de son côté horizontal à son hypoténuse est le même, à savoir cos θ.
Les définitions élémentaires des fonctions sinus et cosinus en termes de côtés d'un triangle rectangle sont :
L'identité pythagoricienne suit en mettant au carré les deux définitions ci-dessus, et en les additionnant, le côté gauche de l'identité devient alors
qui, par le théorème de Pythagore, est égal à 1. Cette définition est valable pour tous les angles, en raison de la définition de définition x= cos θ et y= sin θ pour le cercle unité, ainsi x= c cos θ et y= c sin θ pour un cercle de rayon c, avec x=a et y=b.
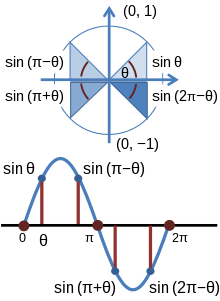
On peut aussi utiliser les identités de symétrie trigonométrique, et les changements et la périodicité. Par les identités de périodicité on peut dire que si la formule est vraie pour -π < θ ≤ π alors elle est vraie pour tout θ réel. Ensuite, nous prouvons l'encadrement π/2 < θ ≤ π, pour ce faire, nous poserons t = θ - π/2. t sera maintenant dans l'intervalle 0 < t ≤ π/2. Nous pouvons alors dire que :
Il ne reste plus qu'à le prouver pour −π < θ < 0. Cela peut être fait en mettant au carré les identités de symétrie pour obtenir
Identités associées
[modifier | modifier le code]
Les identités
et
sont également appelées identités trigonométriques pythagoriciennes. Si un côté d'un triangle rectangle est de longueur 1, alors la tangente de l'angle adjacent à ce côté est la longueur de l'autre côté, et la sécante de l'angle est la longueur de l'hypoténuse.
et
De cette manière, cette identité trigonométrique impliquant la tangente et la sécante découle du théorème de Pythagore. Les identités trigonométriques impliquant la cotangente et la cosécante découle également du théorème de Pythagore.
Le tableau suivant donne les identités avec le facteur ou le diviseur qui les relie à l'identité principale.
| Identité original | Diviseur | Équation divisée | Identité dérivée |
|---|---|---|---|
Preuve utilisant le cercle unité
[modifier | modifier le code]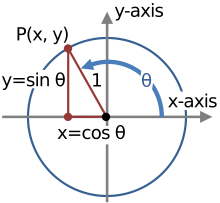
Le cercle unité centré à l'origine du plan euclidien est défini par l'équation[2]:
Soit un angle θ, il y a un unique point P sur le cercle unitaire par rapport à l'axe des abscisses, et les coordonnées x et y de P sont[3]:
Par conséquent, on en déduit,
l'identité pythagoricienne. Puisque les axes sont perpendiculaires, cette identité de Pythagore est en fait équivalente au théorème de Pythagore pour les triangles ayant une longueur d'hypoténuse de 1.
Preuve utilisant les séries entières
[modifier | modifier le code]Les fonctions trigonométriques peuvent également être définies en utilisant des séries entières, à savoir (pour x en radians)[4],[5]:
En utilisant la loi de multiplication formelle pour les séries, on obtient
Dans l'expression de sin2, n doit être au moins supérieur à 1, tandis que dans l'expression de cos2, le coefficient constant est égal à 1. Les termes restants de leur somme sont
par la formule du binôme. Par conséquent,
qui est l'identité trigonométrique pythagoricienne.
Cette définition construit les fonctions sin et cos de manière rigoureuse et prouve qu'elles sont dérivables.
Preuve utilisant une étude de fonction
[modifier | modifier le code]Soit z la fonction qui, à x, associe sin2 x + cos2 x. On note que, pour x = 0, la fonction z prend la valeur 1. Pour prouver l'identité, il suffit de prouver que z est constante, et pour cela, il suffit de vérifier que sa dérivée est nulle. Or :
Donc z = 1 pour tout z. L'identité pythagoricienne est ainsi établie.
Cette preuve de l'identité n'a aucun lien direct avec la démonstration d'Euclide du théorème de Pythagore.
Notes et références
[modifier | modifier le code]- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Pythagorean trigonometric identity » (voir la liste des auteurs).
- (en) Lawrence S. Leff, PreCalculus the Easy Way, Barron's Educational Series, (ISBN 0-7641-2892-2, lire en ligne), p. 296
- Ce résultat peut être trouvé en utilisant la formule pour la distance de l'origine au point (x,y). Voir Cynthia Y. Young, Algebra and Trigonometry, Wiley, 2009 (ISBN 0-470-22273-5), [lire en ligne], p. 210 Cette approche suppose le théorème de Pythagore. Alternativement, on pourrait simplement substituer des valeurs et déterminer que le graphique est un cercle.
- Thomas W. Hungerford, Douglas J. Shaw, Contemporary Precalculus : A Graphing Approach, Cengage Learning, , 1088 p. (ISBN 978-0-495-10833-7 et 0-495-10833-2, lire en ligne), « §6.2 The sine, cosine and tangent functions », p. 442
- James Douglas Hamilton, Time series analysis, Princeton University Press, 1994 (ISBN 0-691-04289-6), [lire en ligne], « Power series », p. 714
- Steven George Krantz, Real analysis and foundations, 2d, 2005, 269–270 p. (ISBN 1-58488-483-5), [lire en ligne], « Definition 10.3 »
























