Lentille mince
Une lentille mince est une lentille dont l'épaisseur reste faible devant les rayons de courbure de ses faces ainsi que devant la différence de ces rayons[1], contrairement aux lentilles épaisses.
Propriétés
[modifier | modifier le code]Dans le cas de la lentille mince, les distances du plan focal objet au centre optique () et du centre optique au plan focal image (), telles qu'indiqué sur la figure, sont égales. est appelé la distance focale de la lentille.
On appelle alors vergence d'une lentille la quantité . Son unité est la dioptrie (symbole δ), homogène à des m−1.
Formules de conjugaison
[modifier | modifier le code]Les formules de conjugaison de Descartes donnent une relation entre les positions sur l'axe optique d'un objet et de son image par rapport au centre optique.
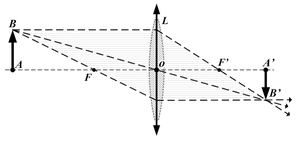
Lorsque les conditions de Gauss sont vérifiées, le système est aplanétique, c'est-à-dire que l'image d'un objet perpendiculaire à l'axe optique est perpendiculaire à l'axe optique: on peut ainsi déterminer la position de l'image d'un point B hors d'axe en considérant l'image du point A qui est la projection de B sur l'axe optique (voir les images ci-dessous).
Notons également qu'un objet à l'infini donnera une image dans le plan focal image de la lentille, un objet placé à 2.f (deux fois la distance focale objet) donnera une image inversée identique à l'objet (grandissement : γ = -1) située à 2.f' (deux fois la distance focale image), au-delà de la distance focale l'objet donnera une image réelle, dans le plan focal l'objet donnera une image à l'infini et entre le foyer image et le centre optique de la lentille l'objet donnera une image virtuelle.
Constructions optiques
[modifier | modifier le code]Pour effectuer des constructions sur un schéma optique, on considère 3 rayons particuliers :
- le rayon passant par le centre optique n'est pas dévié (si le milieu est le même de chaque côté de la lentille) ;
- le rayon parallèle à l'axe avant la lentille est dévié et le rayon sortant passe par le foyer image ;
- le rayon passant par le foyer objet avant la lentille est dévié et ressort parallèle à l'axe.
Ceci permet de construire l'image A'B' d'un petit objet AB perpendiculaire à l'axe optique.
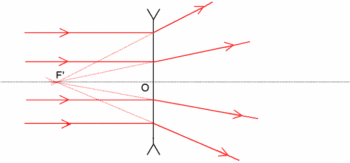
Construction des plaques pour une lentille divergente
[modifier | modifier le code]Construction des rayons pour une lentille convergente
[modifier | modifier le code]Comme le montre la zone rouge sur la première image, tous les rayons issus de B passant par la lentille convergent en B'. Les 3 rayons particuliers permettent de déterminer l'emplacement de B'.
Il faut également noter que des rayons parallèles se coupent au même foyer secondaire. Pour un rayon quelconque, il est ainsi possible de tracer sa propagation après la lentille, en considérant le rayon parallèle qui passe par l'axe optique (et n'est donc pas dévié) : les deux rayons se coupent au niveau du plan focal image.
Notes et références
[modifier | modifier le code]- José-Philippe Pérez, Optique : Fondements et applications [détail des éditions], 5e édition, page 72.