Loi de Gumbel

Gumbel
Densité de probabilité
Fonction de répartition
Paramètres	${\displaystyle \mu \!}$ position (réel) ${\displaystyle \beta >0\!}$ échelle (réel)
Support	${\displaystyle x\in (-\infty ;+\infty )\!}$
Densité de probabilité	${\displaystyle {\frac {\exp(-z)\,z}{\beta }}\!}$ avec ${\displaystyle z=\exp \left[-{\frac {x-\mu }{\beta }}\right]\!}$
Fonction de répartition	${\displaystyle \exp(-\exp[-(x-\mu )/\beta ])\!}$
Espérance	${\displaystyle \mu +\beta \,\gamma \!}$ où ${\displaystyle \gamma }$ est la Constante d'Euler-Mascheroni.
Médiane	${\displaystyle \mu -\beta \,\ln(\ln(2))\!}$
Mode	${\displaystyle \mu \!}$
Variance	${\displaystyle {\frac {\pi ^{2}}{6}}\,\beta ^{2}\!}$
Asymétrie	${\displaystyle {\frac {12{\sqrt {6}}\,\zeta (3)}{\pi ^{3}}}\approx 1.14\!}$
Kurtosis normalisé	${\displaystyle {\frac {12}{5}}}$
Entropie	${\displaystyle \ln(\beta )+\gamma +1\!}$ pour ${\displaystyle \beta >\exp(-(\gamma +1))\!}$
Fonction génératrice des moments	${\displaystyle \Gamma (1-\beta \,t)\,\exp(\mu \,t)\!}$
Fonction caractéristique	${\displaystyle \Gamma (1-i\,\beta \,t)\,\exp(i\,\mu \,t)\!}$
modifier

En théorie des probabilités, la loi de Gumbel (ou distribution de Gumbel), du nom d'Émil Julius Gumbel, est une loi de probabilité continue. La loi de Gumbel est un cas particulier de la loi d'extremum généralisée au même titre que la loi de Weibull ou la loi de Fréchet. La loi de Gumbel est une approximation satisfaisante de la loi du maximum d'un échantillon de variables aléatoires indépendantes toutes de même loi, dès que cette loi appartient, précisément, au domaine d'attraction de la loi de Gumbel. Parmi les lois appartenant au domaine d'attraction de la loi de Gumbel, on compte la loi exponentielle^[1].

La loi de Gumbel peut par exemple servir à prévoir le niveau des crues d'un fleuve, à condition de disposer des mesures des débits maximaux sur une période d'au moins dix ans. Elle peut également servir à prédire la probabilité d'un événement critique, comme un tremblement de terre.

Définitions

Fonction de répartition

Etant donné deux paramètres ${\displaystyle \mu }$ et ${\displaystyle \beta }$, la fonction de répartition de la loi de Gumbel est donné par :

${\displaystyle F(x;\mu ,\beta )=\exp \left(-\exp \left({\frac {\mu -x}{\beta }}\right)\right).}$

Distribution standard de Gumbel

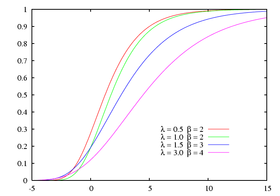
La distribution standard de Gumbel correspond au cas où ${\displaystyle \mu =0}$ et ${\displaystyle \beta =1}$, avec une fonction de répartition cumulative donnée par :

${\displaystyle F(x)=e^{-e^{-x}}\,}$

La fonction densité de probabilité associée est la suivante :

${\displaystyle f(x)=e^{-(x+e^{-x})}.}$

Dans ce cas, le mode est 0, la médiane est ${\displaystyle -\ln(\ln(2))\approx 0.3665}$, la moyenne est ${\displaystyle \gamma \approx 0.5772}$ (la Constante d'Euler-Mascheroni), et l'écart-type est ${\displaystyle \pi /{\sqrt {6}}\approx 1.2825.}$

Les cumulants, pour n > 1, sont donnés par :

${\displaystyle \kappa _{n}=(n-1)!\zeta (n).}$

Propriétés

Le mode est ${\displaystyle \mu }$, tandis que la médiane est ${\displaystyle \mu -\beta \ln \left(\ln 2\right),}$ et l'espérance est donnée par :

${\displaystyle \operatorname {E} (X)=\mu +\gamma \beta }$,

où ${\displaystyle \gamma }$ est la Constante d'Euler-Mascheroni.

L'écart-type ${\displaystyle \sigma }$ est ${\displaystyle \beta \pi /{\sqrt {6}}}$, d'où ${\displaystyle \beta =\sigma {\sqrt {6}}/\pi \approx 0.78\sigma .}$ ^[2]

Au mode, où ${\displaystyle x=\mu }$, la valeur de ${\displaystyle F(x;\mu ,\beta )}$ devient ${\displaystyle e^{-1}\approx 0.37}$, quelle que soit la valeur de ${\displaystyle \beta }$.

Si ${\displaystyle G_{1},\dots ,G_{k}}$ sont des variables aléatoires de Gumbel, indépendantes et identiquement distribuées, avec pour paramètres ${\displaystyle (\mu ,\beta )}$, alors ${\displaystyle \max\{G_{1},\dots ,G_{k}\}}$ suit également une loi de Gumbel avec le jeu de paramètres ${\displaystyle (\mu +\beta \ln k,\beta ).}$

Si ${\displaystyle G_{1},G_{2},\dots }$ sont des variables aléatoires de Gumbel, indépendantes et identiquement distribuées, telles que ${\displaystyle \max\{G_{1},\dots ,G_{k}\}-\beta \ln k}$ a la même distribution que ${\displaystyle G_{1}}$ pour tout entier naturel ${\displaystyle k}$, alors ${\displaystyle G_{1}}$ suit nécessairement une loi de Gumbel avec un paramètre d'échelle ${\displaystyle \beta }$ (Il suffit en fait de considérer seulement deux valeurs distinctes de ${\displaystyle k>1}$ qui sont premières entre elles).

Distributions associées

• Si X suit une loi de Gumbel, alors la distribution conditionnelle de Y = -X dans le cas où Y est strictement positif, ou de façon équivalente, dans le cas où X est strictement négatif, suit une loi de Gompertz. La fonction de répartition G de Y est reliée à F la fonction de répartition de X, par la formule suivante : ${\displaystyle G(y)=\mathbb {P} (Y\leq y)=\mathbb {P} (X\geq -y|X\leq 0)=(F(0)-F(-y))/F(0)}$ pour y > 0. Les densités sont donc reliées par ${\displaystyle g(y)=f(-y)/F(0)}$ : la densité de Gompertz (en) est proportionnelle à la densité de Gumbel réfléchie et restreinte aux valeurs strictement positives^[3].
• Si X suit une exponentielle de moyenne égale à 1, alors –log(X) suit une distribution standard de Gumbel.
• Si ${\displaystyle X,Y\sim \mathrm {Gumbel} (\alpha ,\beta )}$ alors ${\displaystyle X-Y\sim \mathrm {Logistic} (0,\beta )\,}$.

La théorie associée aux lois log-gamma multivariées généralisées (en) fournit une version multivariée de la loi de Gumbel.

Occurrence et applications

Ajustement d'une loi de Gumbel à partir de données observées (maximums journaliers des cumuls de précipitations)

Gumbel a montré que la valeur maximale (ou dernier statistique d'ordre) dans un échantillon de variable aléatoires suivant une distribution exponentielle, moins le logarithme naturel de la taille de l’échantillon^[4], tend vers la distribution de Gumbel à mesure que la taille de l’échantillon augmente^[5].

Concrètement, soit ${\displaystyle \rho (x)=e^{-x}}$ la distribution de probabilité de ${\displaystyle x}$ et ${\displaystyle Q(x)=1-e^{-x}}$ sa fonction de répartition. Alors, la valeur maximale parmi ${\displaystyle N}$ réalisations de ${\displaystyle x}$ est inférieure à ${\displaystyle X}$ si et seulement si toutes les réalisations sont inférieures à ${\displaystyle X}$. Ainsi, la fonction de répartition de la valeur maximale ${\displaystyle {\tilde {x}}}$ satisfait :

${\displaystyle P({\tilde {x}}-\log(N)\leq X)=P({\tilde {x}}\leq X+\log(N))=[Q(X+\log(N))]^{N}=\left(1-{\frac {e^{-X}}{N}}\right)^{N},}$

et, pour une valeur importante de ${\displaystyle N}$, le membre de droite converge vers ${\displaystyle e^{-e^{(-X)}}.}$

En hydrologie, la distribution de Gumbel est donc utilisée pour analyser des variables telles que les valeurs maximales mensuelles et annuelles des précipitations journalières et des débits fluviaux^[2], ainsi que pour décrire les périodes de sécheresse^[6].

Gumbel a également montré que l'estimateur ^r⁄_(n+1) pour la probabilité d’un événement — où r est le rang de la valeur observée dans la série de données et n est le nombre total d'observations — est un estimateur non biaisé de la probabilité cumulative autour du mode de la distribution. Par conséquent, cet estimateur est souvent utilisé pour tracer les courbes.

En théorie des nombres, la distribution de Gumbel approxime le nombre de termes dans une partition d'un entier aléatoire^[7] ainsi que la taille ajustée des tendances des écarts entre nombres premiers et des écarts maximaux entre les constellations de nombres premiers^[8].

Elle apparaît également dans le problème du collectionneur de coupons.

Astuces de reparamétrisation de Gumbel

En apprentissage automatique, la distribution de Gumbel est parfois utilisée pour générer des échantillons à partir de la distribution catégorielle. Cette technique est appelée "astuce de Gumbel-max" et est un exemple particulier des "astuces de reparamétrisation"^[9].

En détail, soit ${\displaystyle (\pi _{1},\ldots ,\pi _{n})}$ des valeurs non négatives, non nulles, et soit ${\displaystyle g_{1},\ldots ,g_{n}}$ des échantillons indépendants de Gumbel(0, 1). Alors, par une intégration de routine, on a : $${\displaystyle \Pr(j=\arg \max _{i}(g_{i}+\log \pi _{i}))={\frac {\pi _{j}}{\sum _{i}\pi _{i}}}}$$ C'est-à-dire, ${\displaystyle \arg \max _{i}(g_{i}+\log \pi _{i})\sim {\text{Categorical}}\left({\frac {\pi _{j}}{\sum _{i}\pi _{i}}}\right)_{j}}$.

De manière équivalente, étant donné ${\displaystyle x_{1},...,x_{n}\in \mathbb {R} }$, on peut échantillonner à partir de sa distribution de Boltzmann via : $${\displaystyle \Pr(j=\arg \max _{i}(g_{i}+x_{i}))={\frac {e^{x_{j}}}{\sum _{i}e^{x_{i}}}}}$$ Des équations connexes incluent^[10] :

• Si ${\displaystyle x\sim \operatorname {Exp} (\lambda )}$, alors ${\displaystyle (-\ln x-\gamma )\sim {\text{Gumbel}}(-\gamma +\ln \lambda ,1)}$.
• ${\displaystyle \max _{i}(g_{i}+\log \pi _{i})\sim {\text{Gumbel}}\left(\log \left(\sum _{i}\pi _{i}\right),1\right)}$.
• ${\displaystyle \mathbb {E} [\max _{i}(g_{i}+\beta x_{i})]=\log \left(\sum _{i}e^{\beta x_{i}}\right)+\gamma .}$

Génération de variables aléatoires

Puisque la fonction quantile (fonction inverse de la fonction de répartition), ${\displaystyle Q(p)}$, d'une distribution de Gumbel est donnée par :

${\displaystyle Q(p)=\mu -\beta \ln(-\ln(p)),}$

la variable aléatoire ${\displaystyle Q(U)}$ suit une distribution de Gumbel avec les paramètres ${\displaystyle \mu }$ et ${\displaystyle \beta }$ lorsque la variable aléatoire ${\displaystyle U}$ est tirée de la loi uniforme sur l'intervalle ${\displaystyle (0,1)}$.

Ajustement graphique de la loi de Gumbel

Exemple d’un ajustement graphique de la loi de Gumbel (Cours L.Neppel)

Avant l’ère des logiciels, le papier probabiliste était utilisé pour représenter la distribution de Gumbel (voir illustration). Le graphique est basé sur la linéarisation de la fonction de répartition ${\displaystyle F}$ :

${\displaystyle -\ln[-\ln(F)]={\frac {x-\mu }{\beta }}}$

Sur le graphique, l'axe horizontal est construit avec une échelle logarithmique double. L'axe vertical est linéaire. En reportant ${\displaystyle F}$ sur l'axe horizontal du papier et la variable ${\displaystyle x}$ sur l'axe vertical, la distribution est représentée par une droite de pente 1${\displaystyle /\beta }$. Lorsque des logiciels d’ajustement de distribution comme CumFreq sont devenus disponibles, la tâche de représentation graphique de la distribution a été facilitée.

Voir aussi

• Loi d'extremum généralisée
• Graphe aléatoire
• Problème du collectionneur de vignettes

Notes

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Gumbel distribution » (voir la liste des auteurs).

1. Regular variation, Bingham, Goldie et Teugels.
2. R.J. Oosterbaan, Drainage Principles and Applications, Publication 16, Wageningen, The Netherlands, International Institute for Land Reclamation and Improvement (ILRI), 1994, 175–224 (ISBN 90-70754-33-9, lire en ligne), « Chapter 6 Frequency and Regression Analysis »
3. W.J. Willemse et R. Kaas, « Rational reconstruction of frailty-based mortality models by a generalisation of Gompertz' law of mortality », Insurance: Mathematics and Economics, vol. 40, n^o 3,‎ 2007, p. 468 (DOI 10.1016/j.insmatheco.2006.07.003)
4. « Distribution de Gumbel et distribution exponentielle », sur Mathematics Stack Exchange
5. E.J. Gumbel, Statistical theory of extreme values and some practical applications, vol. 33, U.S. Department of Commerce, National Bureau of Standards, coll. « Applied Mathematics Series », 1954, 1re éd. (ASIN B0007DSHG4, lire en ligne)
6. Eleanor J. Burke, Richard H.J. Perry et Simon J. Brown, « Analyse des valeurs extrêmes des sécheresses au Royaume-Uni et projections futures », Journal of Hydrology, vol. 388, n^os 1–2,‎ 2010, p. 131–143 (DOI 10.1016/j.jhydrol.2010.04.035, Bibcode 2010JHyd..388..131B)
7. Paul Erdös et Joseph Lehner, « La distribution du nombre de termes dans les partitions d'un entier positif », Duke Mathematical Journal, vol. 8, n^o 2,‎ 1941, p. 335 (DOI 10.1215/S0012-7094-41-00826-8)
8. A. Kourbatov, « Écarts maximaux entre les k-uplets de nombres premiers : une approche statistique », Journal of Integer Sequences, vol. 16,‎ 2013 (Bibcode 2013arXiv1301.2242K, arXiv 1301.2242) Article 13.5.2.
9. Eric Jang, Shixiang Gu et Ben Poole « Reparamétrisation catégorielle avec Gumbel-Softmax » (Avril 2017) (lire en ligne)
   —International Conference on Learning Representations (ICLR) 2017
10. (en) Matej Balog, Nilesh Tripuraneni, Zoubin Ghahramani et Adrian Weller, « Les parents oubliés de l'astuce de Gumbel », PMLR,‎ 17 juillet 2017, p. 371–379 (arXiv 1706.04161, lire en ligne)

Bibliographie

• (en) N. H. Bingham, C. M. Goldie et J. L. Teugels, Regular Variation, Cambridge, Cambridge University Press, coll. « Encyclopedia of Mathematics and its Applications » (n^o 27), juin 1989, 1^re éd., 516 p. (ISBN 978-0-521-37943-4, DOI 10.2277/0521379431, lire en ligne)

• Portail des probabilités et de la statistique