Méthode de Simpson

En analyse numérique, la méthode de Simpson, du nom de Thomas Simpson, est une technique de calcul numérique d'une intégrale, c'est-à-dire le calcul approché de :

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x}$

Cette méthode utilise l'approximation d'ordre 2 de f par un polynôme quadratique P prenant les mêmes valeurs que f aux points d'abscisse a, b et m = ^{(a + b)}⁄₂. Pour déterminer l'expression de cette parabole (polynôme de degré 2), on utilise l'interpolation lagrangienne. Le résultat peut être mis sous la forme :

${\displaystyle P(x)=f(a){\frac {(x-m)(x-b)}{(a-m)(a-b)}}+f(m){\frac {(x-a)(x-b)}{(m-a)(m-b)}}+f(b){\frac {(x-a)(x-m)}{(b-a)(b-m)}}.}$

Un polynôme étant une fonction très facile à intégrer, on approche l'intégrale de la fonction f sur l'intervalle [a, b], par l'intégrale de P sur ce même intervalle. On a ainsi la simple formule :

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x\approx \int _{a}^{b}P(x)\,\mathrm {d} x={\frac {b-a}{6}}\left[f(a)+4f\left({\frac {a+b}{2}}\right)+f(b)\right].}$

La courbe rouge représente le polynôme d'approximation P(x).

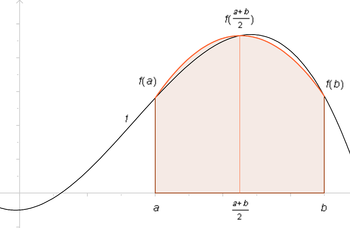
Un autre moyen d'arriver à ce résultat est d'appliquer les formules de Newton-Cotes avec n = 2.

Si f est 4 fois continument différentiable sur [a, b], l'erreur d'approximation vaut :

${\displaystyle -{\frac {h^{5}}{90}}f^{(4)}(\xi ),\xi \in [a,b]}$ où ${\displaystyle h={\frac {b-a}{2}}.}$

Cette expression du terme d'erreur signifie que la méthode de Simpson est exacte (c'est-à-dire que le terme d'erreur s'annule) pour tout polynôme de degré inférieur ou égal à 3. De plus, cette méthode est d'ordre 4 pour toute fonction continûment dérivable quatre fois sur [a, b].

Forme composite

Par ailleurs, il apparaît que plus l'intervalle est petit, plus l'approximation de la valeur de l'intégrale est bonne. Par conséquent, pour obtenir un résultat correct, on subdivise l'intervalle [a, b] en sous-intervalles et on additionne la valeur obtenue sur chaque intervalle. Soit :

${\displaystyle \int _{a}^{b}f(x)\,\mathrm {d} x\approx {\frac {h}{6}}\left[f(x_{0})+2\sum _{j=1}^{n-1}f(x_{2j})+4\sum _{j=1}^{n}f(x_{2j-1})+f(x_{2n})\right],}$

où :

• n est le nombre de sous-intervalles de [a, b] ;
• h =^{(b – a)}⁄_n est la longueur de ces sous-intervalles ;
• ${\displaystyle x_{i}=a+i{\frac {h}{2}}}$ pour ${\displaystyle i=0,1,\dots ,2n-1,2n.}$

Pour cette formule composite, le terme d'erreur devient égal à

${\displaystyle -n\times {\frac {h^{5}}{2880}}f^{(4)}(\xi '),\xi '\in [a,b],}$

ce qui signifie que la méthode composite fournit aussi des résultats exacts pour des polynômes de degré inférieur ou égal à 3.

À la fois à cause de sa simplicité de mise en œuvre et sa bonne précision, cette méthode est la plus utilisée par les calculatrices pour tous calculs approchés d'intégrales de fonctions explicites.

Méthode 3/8 de Simpson

La méthode 3/8 de Simpson, ou deuxième méthode de Simpson, s'appuie cette fois sur une approximation cubique de la fonction plutôt qu'une approximation quadratique : $${\displaystyle {\begin{aligned}\int _{a}^{b}f(x)\,\mathrm {d} x&\approx {\frac {3}{8}}h\left[f(a)+3f\left({\frac {2a+b}{3}}\right)+3f\left({\frac {a+2b}{3}}\right)+f(b)\right]\\&={\frac {b-a}{8}}\left[f(a)+3f\left({\frac {2a+b}{3}}\right)+3f\left({\frac {a+2b}{3}}\right)+f(b)\right],\end{aligned}}}$$ où ${\displaystyle h=(b-a)/3}$ est le pas.

L'erreur est donnée par $${\displaystyle -{\frac {3}{80}}h^{5}f^{(4)}(\xi )=-{\frac {(b-a)^{5}}{6480}}f^{(4)}(\xi ),}$$ où ${\displaystyle \xi \in [a,b]}$. La méthode 3/8 est donc deux fois plus précise que la méthode classique, mais nécessite une évaluation supplémentaire de la fonction^[1].

Pour une formule basée sur une interpolation d'ordre supérieur, on pourra se tourner vers les formules de Newton-Cotes.

On peut également dériver la formule 3/8 de Simpson pour en tirer une forme composite : $${\displaystyle {\begin{aligned}\int _{a}^{b}f(x)\,\mathrm {d} x&\approx {\frac {3}{8}}h\sum _{i=1}^{n/3}\left[f(x_{3i-3})+3f(x_{3i-2})+3f(x_{3i-1})+f(x_{3i})\right]\\&={\frac {3}{8}}h\left[f(x_{0})+3f(x_{1})+3f(x_{2})+2f(x_{3})+3f(x_{4})+3f(x_{5})+2f(x_{6})+\dots +2f(x_{n-3})+3f(x_{n-2})+3f(x_{n-1})+f(x_{n})\right]\\&={\frac {3}{8}}h\left[f(x_{0})+3\sum _{i=1,\ 3\nmid i}^{n-1}f(x_{i})+2\sum _{i=1}^{n/3-1}f(x_{3i})+f(x_{n})\right].\end{aligned}}}$$

L'erreur est évaluée avec^[1] ${\displaystyle -{\frac {1}{80}}h^{4}(b-a)f^{(4)}(\xi ),}$ mais il apparait clairement que la formule n'est utilisable pour n multiple de 3.

Références

1. John H. Matthews, « Simpson's 3/8 Rule for Numerical Integration » [archive du 4 décembre 2008], sur Numerical Analysis - Numerical Methods Project, California State University, Fullerton, 2004 (consulté le 11 novembre 2008)

Voir aussi

Article connexe

Calcul intégral

Liens externes

• Formules de Newton-Cotes sur math-linux.com
• (en) Eric W. Weisstein, « Simpson's Rule », sur MathWorld
• (en) Eric W. Weisstein, « Simpson's 3/8 Rule », sur MathWorld

• Portail de l'analyse