Modèle d'évaluation des actifs financiers
Le modèle d'évaluation des actifs financiers (MEDAF, ou en anglais Capital asset pricing model) est un modèle financier qui fournit une estimation du taux de rentabilité attendu par le marché pour un actif financier en fonction de son risque systématique.
Définition
[modifier | modifier le code]Le MEDAF ou capital asset pricing model explique la réalisation de l'équilibre du marché par l'offre et la demande pour chaque titre. Il permet de déterminer la rentabilité d'un actif risqué par son risque systématique. MEDAF est une traduction approximative de la version anglophone[1]. Une traduction plus fidèle et issue des milieux académiques français[2] est le modèle d'équilibre des actifs financiers, qui partage le même acronyme.
Les transactions cesseront lorsque les opérateurs auront un portefeuille identique.
La formule est une fonction :
- de la mesure du risque systématique de l'actif, c'est-à-dire au risque non diversifiable (l'investisseur diversifiera son portefeuille directement sur le marché), noté (coefficient bêta de l'actif) ;
- de la rentabilité espérée sur le marché, notée ;
- du taux d'intérêt sans risque (généralement des emprunts d'État ou de la banque centrale), noté .
représente la prime de risque du marché, c'est-à-dire le surplus de rentabilité exigé par les investisseurs lorsque ces derniers placent leur argent sur le marché, plutôt que dans un actif sans risque.
Le est la volatilité de la rentabilité de l'actif considéré rapportée à celle du marché. Mathématiquement parlant, elle correspond au rapport entre la covariance de la rentabilité de l'actif et de la rentabilité du marché et la variance de la rentabilité du marché.
Dans le modèle MEDAF (ou CAPM), on peut montrer que ce coefficient correspond à l'élasticité du cours du titre par rapport à l'indice boursier représentant le marché.
où représente le risque du marché (l'écart-type de ) et le risque de l'actif (l'écart-type de la rentabilité attendue de l'actif). Ainsi, un actif représentant le marché aura un égal à 1. Pour un actif sans risque, il sera égal à 0.
Historique
[modifier | modifier le code]Le MEDAF a été introduit par Jack L. Treynor dans un article de 1961, puis de 1962[3]. Il est repris par William F. Sharpe (1964), John Lintner (1965) et Jan Mossin (1966) indépendamment, en poursuivant les travaux initiaux de Harry Markowitz sur la diversification et la théorie moderne du portefeuille. Sharpe, Markowitz et Merton Miller ont reçu conjointement le prix Nobel d'économie pour leur contribution à la science financière. L'hypothèse d'efficience du marché financier, due à Eugène Fama, a notamment servi aux travaux ayant abouti au MEDAF.
Hypothèses
[modifier | modifier le code]Le MEDAF postule les hypothèses théoriques suivantes[4] :
- Il n'y a pas de coûts de transaction (c'est-à-dire ni commission sur les transactions, ni marge entre prix d'achat et de vente).
- Un investisseur peut acheter ou vendre à découvert n'importe quelle action sans que cela ait une incidence sur le prix de l'action.
- Il n'y a pas de taxes, la fiscalité est donc la même pour les plus-values et les dividendes.
- Les investisseurs n'aiment pas le risque.
- Les investisseurs ont le même horizon temporel.
- Tous les investisseurs ont un portefeuille de Markowitz car ils ne considèrent chaque action que sous son aspect moyenne-variance.
- Les investisseurs contrôlent le risque par la diversification.
- Tous les actifs, y compris le capital humain, peuvent être achetés et vendus librement sur le marché.
- Les investisseurs peuvent prêter ou emprunter de l'argent au taux sans risque.
Droite de marché des capitaux (CML)
[modifier | modifier le code]On peut représenter graphiquement le modèle CAPM. Prenons tout d’abord la droite de marché des capitaux (capital market line (CML) en anglais). Un investisseur considère le rendement espéré [E(R)] et le risque (la variabilité représentée par l’écart-type du portefeuille,). Pour un risque donné, il préfère le portefeuille qui a le rendement le plus élevé. Parmi tous les portefeuilles possibles, Markowitz propose de calculer ceux qui ont le rendement le plus élevé pour un risque donné. On obtient alors la frontière de Markowitz A-B. Les portefeuilles efficients se trouvent sur cette courbe qui est la même pour tous les investisseurs (mêmes anticipations des rendements et des risques).
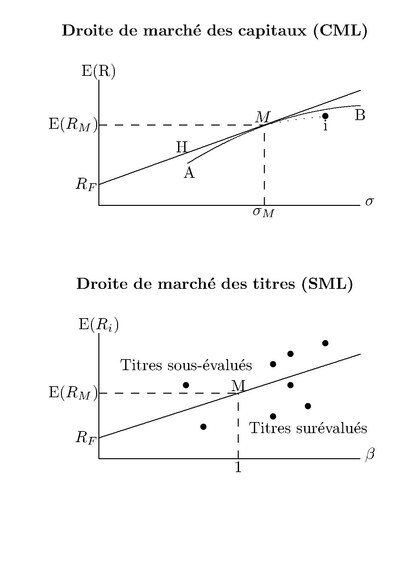
Soit le rendement du titre sans risque (par exemple, les bons du trésor des États-Unis coupon zéro). La droite de marché des capitaux part de et est tangente à la courbe A-B. Un investisseur peut choisir tout portefeuille sur la droite entre et M. Tous les investisseurs doivent posséder le portefeuille de marché M dans des proportions plus ou moins grandes. Par exemple, le portefeuille H comprend en part égale le titre sans risque et le portefeuille M.
Soit le portefeuille P composé du portefeuille de marché M (dont le rendement est ) dans la proportion w et du titre sans risque dans la proportion 1-w. Le rendement espéré est :
et sa variance :
En introduisant la valeur de w de cette équation dans celle du rendement espéré on obtient l’équation de la droite de marché des capitaux :
Droite de marché des titres (SML)
[modifier | modifier le code]Le risque du portefeuille de marché est :
où (ou ) est la part du titre i (ou j) dans le portefeuille du marché et N le nombre de titres.
La covariance entre un titre i et le portefeuille de marché est :
On peut alors écrire le risque du portefeuille de marché de la manière suivante :
Prenons maintenant le cas du titre . Soient tous les portefeuilles composés du titre dans des proportions variables () et le reste dans le portefeuille de marché. Le rendement espéré de ces portefeuilles sera :
et le risque :
Ces portefeuilles se trouvent sur la ligne pointillée . La pente de cette ligne est[5] :
Lorsque , et la pente est celle de la droite - M. En utilisant cette relation et l’équation de la droite du marché des capitaux on obtient :
qui est la droite de marché des titres (security market line (SML) en anglais). Soit :
où est le coefficient de corrélation entre le titre i et le portefeuille de marché. On peut écrire :
À l’équilibre, les rendements espérés de tous les titres doivent se trouver sur cette droite. Si le rendement est supérieur à la valeur d’équilibre, on dit que le titre est sous-évalué. Au contraire, si le rendement est au-dessous de la valeur d’équilibre le titre est surévalué. On calcule souvent la valeur alpha :
où est la valeur d’équilibre selon le modèle CAPM.
Le coefficient est un indice de risque systématique. Le marché récompense uniquement ce risque. Si l’investisseur n’a pas diversifié son portefeuille, le risque supplémentaire n’est pas récompensé. Une valeur de supérieure à l’unité signifie que le rendement du titre varie plus fortement que celui du portefeuille de marché.
Critiques
[modifier | modifier le code]La plupart des hypothèses sur lesquelles se base le MEDAF ne sont pas vérifiées dans la réalité, en particulier les hypothèses numéro 2, 6 et 9 :
- Toute transaction d'une certaine taille a un effet sur le prix d'une action
- Peu d'investisseurs ont un portefeuille de Markowitz (l'inventeur de ce portefeuille, Harry Markowitz, lui-même, ne l'utilise pas [6] ; George Akerlof non plus[7])
- L'hypothèse numéro 9 stipule qu'un investisseur peut emprunter de l'argent sans aucune limite, ce qu'aucune banque n'autorise aujourd'hui.
Harry Markowitz, dans un article de 2005 du Financial Analysts Journal, a remarqué que si l'on modifie l'hypothèse numéro 9 du MEDAF, alors les conclusions de son modèle sont modifiées drastiquement[8].
Toutefois, les résultats du MEDAF en font un modèle très utilisé dans le secteur financier[4].
Extensions
[modifier | modifier le code]Plusieurs modifications du modèle CAPM ont été proposées avec des hypothèses moins restrictives. Le modèle zero-beta de Fischer Black[9] tient compte de l’impossibilité d’investir au taux d’intérêt sans risque. John Lintner[10] présente un modèle où les anticipations ne sont pas homogènes. Fama[11] examine le cas d’un investisseur dont les choix ne se limitent pas à une seule période.
Notes et références
[modifier | modifier le code]- ↑ Pricing signifie formation du prix et non pas évaluation. D'ailleurs certains auteurs préfèrent la traduction modèle d'équilibre des actifs financiers
- ↑ Florin Aftalion, La nouvelle finance et la gestion des portefeuilles, Paris, Economica, 2008 3e édition, 248 p. (ISBN 978-2-7178-5540-1), pages 75 à 98
- ↑ (en) French, Craig W., « The Treynor Capital Asset Pricing Model », sur ssrn.com (consulté le ).
- Richard A. Brealey, Principles of corporate finance, (ISBN 978-1-265-07415-9, 1-265-07415-1 et 978-1-264-08094-6, OCLC 1309100489, lire en ligne)
- ↑ Il convient d’utiliser la relation :
- ↑ Interrogé sur la façon dont il plaçait ses fonds, il répondit : « Mon intention est de ne pas avoir de regrets dans le futur. J'investis 50 % dans des obligations, 50 % dans des actions », Behavorial Investing, James Montier, Wiley Finance, 2007, page 431
- ↑ George Akerlof place une part importante de son argent dans des fonds commun de placement, Behavorial Investing, James Montier, Wiley Finance, 2007, page 431
- ↑ Article de Markowitz dans FAJ
- ↑ Black Fischer (1972), Capital market Equilibrium with Restricted Borrowing, Journal of Business, pp. 444-455
- ↑ Lintner John (1969),The Aggregation of Investors Diverse Judgments and Preferences in Purely Competitive Security Markets, Journal of Financial and Quantitative Analysis, pp.347-400
- ↑ Fama Eugene (1970), Multi-Period Consumption-Investment Decision, American Economic Review, pp.163-174
Voir aussi
[modifier | modifier le code]Articles connexes
[modifier | modifier le code]Modèles d'évaluation
[modifier | modifier le code]- Modèle d'évaluation des actifs basé sur la consommation
- Modèle intertemporel d'évaluation des actifs
- Modèle d'évaluation par arbitrage (APT)
- Modèle Fama-French à trois facteurs
Autres articles
[modifier | modifier le code]- Portefeuille de Markowitz
- Coefficient bêta
- Évaluation financière
- Théorie moderne du portefeuille
- Efficience du marché financier
- Allocation d'actifs
- Flux de trésorerie disponible
- Évaluation du prix d'une action
Bibliographie
[modifier | modifier le code]- Black, Fischer., Michael C. Jensen, and Myron Scholes (1972). The Capital Asset Pricing Model: Some Empirical Tests, pp. 79–121 in M. Jensen ed., Studies in the Theory of Capital Markets. New York: Praeger Publishers.
- Fama, Eugene F. (1968). Risk, Return and Equilibrium: Some Clarifying Comments. Journal of Finance Vol. 23, No. 1, pp. 29–40.
- (en) Eugene F. Fama et Kenneth R. French, « The Cross-Section of Expected Stock Returns », Journal of Finance, vol. 47, no 2, , p. 427–465 (DOI 10.2307/2329112)
- French, Craig W. (2003). The Treynor Capital Asset Pricing Model, Journal of Investment Management, Vol. 1, No. 2, pp. 60–72. Available at http://www.joim.com/
- French, Craig W. (2002). Jack Treynor's 'Toward a Theory of Market Value of Risky Assets' (December). Available at http://ssrn.com/abstract=628187
- Lintner, John (1965). The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets, Review of Economics and Statistics, 47 (1), 13-37.
- Markowitz, Harry M. (1999). The early history of portfolio theory: 1600-1960, Financial Analysts Journal, Vol. 55, No. 4
- Mehrling, Perry (2005). Fischer Black and the Revolutionary Idea of Finance. Hoboken: John Wiley & Sons, Inc.
- Mossin, Jan. (1966). Equilibrium in a Capital Asset Market, Econometrica, Vol. 34, No. 4, pp. 768–783.
- Ross, Stephen A. (1977). The Capital Asset Pricing Model (CAPM), Short-sale Restrictions and Related Issues, Journal of Finance, 32 (177)
- Rubinstein, Mark (2006). A History of the Theory of Investments. Hoboken: John Wiley & Sons, Inc.
- Sharpe, William F. (1964). Capital asset prices: A theory of market equilibrium under conditions of risk, Journal of Finance, 19 (3), 425-442
- Stone, Bernell K. (1970) Risk, Return, and Equilibrium: A General Single-Period Theory of Asset Selection and Capital-Market Equilibrium. Cambridge: MIT Press.
- Tobin, James (1958). Liquidity preference as behavior towards risk, The Review of Economic Studies, 25
- Treynor, Jack L. (1961). Market Value, Time, and Risk. Unpublished manuscript.
- Treynor, Jack L. (1962). Toward a Theory of Market Value of Risky Assets. Unpublished manuscript. A final version was published in 1999, in Asset Pricing and Portfolio Performance: Models, Strategy and Performance Metrics. Robert A. Korajczyk (editor) London: Risk Books, pp. 15–22.
- Mullins, David W. (1982). Does the capital asset pricing model work?, Harvard Business Review, January–February 1982, 105-113.
- Prince,Kudzai Hwenjere. (2010). Capital Markets in the World and Raising markets in Zimbabwe, National University of Science Technology. Bcom Banking, 2010



![{\displaystyle E(R_{actif})=R_{F}+\beta _{actif}\cdot [E(R_{M})-R_{F}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43509ad1dda59a004645dc866ee81347f3913cb9)
![{\displaystyle [E(R_{M})-R_{F}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d045d4e2997ee924a6a1318190e1441eb4804ef6)










![{\displaystyle E(R_{P})=R_{F}+\left[E(R_{M})-R_{F}\right]{\frac {\sigma _{P}}{\sigma _{M}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7c3e9aa1cd3ade78786d796365844eb1277696e3)
![{\displaystyle \sigma _{M}=\left[\sum _{i}^{N}\sum _{j}^{N}\omega _{i}\omega _{j}\sigma _{ij}\right]^{0.5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1663f639eca950468cc5bee409e414df4452a03d)









![{\displaystyle \sigma _{Q}=\left[x^{2}\sigma _{i}^{2}+(1-x)^{2}\sigma _{M}^{2}+2x(1-x)\sigma _{iM}\right]^{0.5}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2a924ed508dfa32847d2e78437de05054ca22e0)

![{\displaystyle {\frac {\mathrm {d} E(R_{Q})}{\mathrm {d} \sigma _{Q}}}={\frac {\left[E(R_{i})-E(R_{M})\right]\left[x^{2}\sigma _{i}^{2}+(1-x)^{2}\sigma _{M}^{2}+2x(1-x)\sigma _{iM}\right]^{0.5}}{x\sigma _{i}^{2}-(1-x)\sigma _{M}^{2}+(1-2x)\sigma _{iM}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88441273809d4dd1e42af2ab92cd2b54471567e4)


![{\displaystyle E(R_{i})=R_{F}+\left[{\frac {E(R_{M})-R_{F}}{\sigma _{M}^{2}}}\right]\sigma _{iM}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9d5b4f5bb2060529fc7f7d9abb532c2097dcaee)


![{\displaystyle E(R_{i})=R_{F}+\beta _{i}\left[E(R_{M})-R_{F}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d87786a20741d1ff9ab4ff076d1bb4489123508)



