Monocorde

Le monocorde est un instrument de mesure des intervalles des gammes musicales. Il est constitué d'une caisse de résonance sur laquelle une corde tendue entre deux sillets est divisée par un chevalet mobile.
Les rapports de distances entre les différentes partitions de la corde construisent de la sorte une échelle musicale.
Histoire
[modifier | modifier le code]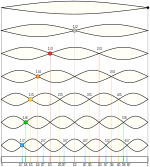
Boèce attribue l'invention du monocorde en tant qu'instrument expérimental à Pythagore[1], mais il existait probablement avant en Égypte[2].
Pythagore a fait la démonstration que la hauteur , du son est inversement proportionnelle à la longueur de la corde[réf. nécessaire]. De cette expérience, Pythagore tire les conclusions suivantes :
- En plaçant le chevalet au milieu de la corde — donc, en divisant celle-ci en deux parties égales —, la corde en question fait entendre l'octave supérieure du son de la corde "à vide" (c'est-à-dire non divisée) alors que les mise en vibration des deux parties égales de la corde situées de part et d'autre du chevalet, fait entendre l'unisson.
- De la même façon, en plaçant le chevalet au tiers de la corde — donc, en divisant celle-ci en trois —, la corde en question donne alors le redoublement de la quinte supérieure du son initial (autrement dit, la « douzième supérieure »). De l'autre côté du chevalet, avec une longueur de , on obtient "tout naturellement" la quinte supérieure du son initial.
Montage du canon harmonique
[modifier | modifier le code]
Le « canon harmonique », ou monocorde, est, au minimum, « simplement une corde sous laquelle se trouve une planche de même longueur, sur laquelle peuvent être délimités les points auxquels la corde doit être arrêtée pour donner certaines notes », ce qui permet les comparaisons[4].
Une corde est fixée aux deux extrémités et tendue au-dessus d'une caisse de résonance. Un ou plusieurs chevalets mobiles sont ensuite manipulés pour démontrer les relations mathématiques entre les fréquences produites. « Avec sa corde unique, son chevalet mobile et sa règle graduée, le monocorde (kanōn [grec : loi]) se situait à cheval entre les notes et les nombres, les intervalles et les rapports, la perception sensorielle et la raison mathématique[5]. » Cependant, « la musique, les mathématiques et l'astronomie étaient [également] inexorablement liées dans le monocorde[6]. » En tant qu'outil pédagogique pour démontrer les relations mathématiques entre les intervalles, le monocorde est resté en usage tout au long du Moyen Âge[7].
Théorie
[modifier | modifier le code]
En divisant la corde en intervalles égaux de 2 à 6 on obtient les principaux accords purs[2] :
- par 2 : c'est l'octave supérieure par rapport à la corde entière (rapport de hauteur 2/1) ;
- par 3 : c'est la quinte (rapport de hauteur 3/2, c'est-à-dire qu'on multiplie la fréquence de la fondamentale par 3/2 pour obtenir celle de la quinte : si la longueur = 2/3, alors la hauteur = 1/L = 3/2)
- par 4 : c'est la quarte (rapport 4/3) ;
- par 5 : c'est la tierce majeure (rapport 5/4) ;
- par 6 : c'est la tierce mineure (rapport 6/5).
Soit la longueur de la corde, et sa fréquence ; Pythagore a donc remarqué[réf. nécessaire]que .
On remarque aussi que
Comme , la pratique arithmétique grecque fait noter les nombres rationnels plus grands que 1 comme 1 + X.
En posant , on obtient
d'où on déduit , la notation revient donc à nommer X, depuis X = 0 pour le do à X=1 pour le do de l'octave supérieur.
On déduit aussi :
et
Pour un donné, on voit que la corde est partagée en deux longueurs : et
Or
Par exemple, si la corde à vide donne un Do, le Sol a pour fréquence N = No (1 + 1/2). Il se joue donc avec la frette au [(1/2/(1+1/2)]=1/3 de la longueur.
Les sept notes de la gamme correspondaient à des rationnels "simples" et approximatifs d'une assonance.
Le tableau ci-après donne les valeurs X, encadrant 1+1/2 == 1+5/10(qu'on pourra réduire aisément) et les écarts (rapport de fréquences de deux notes consécutives) ; il apparaît que ces écarts ne sont évidemment pas constants, et il y a un problème à régler simplement l'écart entre les notes (l'écart musical , irrationnel, conduira à la crise majeure des mathématiques, appelée crise pythagoricienne).
| Note | do | ré | mi | fa | sol | la | si | do | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X | 0 | 1/8 | 1/4 | 1/3 | 1/2 | 2/3 | 7/8 | 1 | ||||||||
| 1 + X | 1 | 1 + 1/8 | 1 + 2/8 | 1 + 3/9 | 1 + 5/10 | 2 - 3/9 | 2 - 1/8 | 2 | ||||||||
| Rapport | 1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2 | ||||||||
| Ecarts | 9/8 | 10/9 | 9/8 | 10/9 | 9/8 | |||||||||||

Instruments de musique monocorde
[modifier | modifier le code]
Les parties d'un monocorde comprennent une cheville, un sillet, une corde, un chevalet mobile, un chevalet fixe, des marques de calibrage, une caisse ou boîte de résonance, et une pique[6].
Les instruments dérivés du monocorde (ou de son chevalet mobile) comprennent le guqin, le Đàn bầu, le koto, la vina, la vielle à roue et le clavicorde ("d'où tous les instruments à clavier")[6]. Un monopipe est la version pour instrument à vent d'un monocorde ; un tuyau à ouverture variable qui peut produire des hauteurs variables, un cylindre coulissant avec les chiffres du monocorde marqués[8]. Une correction de l'extrémité d'un tuyau ouvert (en) doit être utilisée avec cette méthode, pour atteindre la précision de la hauteur de la note produite.
Notes et références
[modifier | modifier le code]- Jean-Marc Warszawski, « Boèce (480-524) », sur musicologie.org, (consulté le ).
- Abromont 2001, p. 334
- (en) Sir James Jeans (1937/1968), Science & Music, Dover (ISBN 0-486-61964-8), p. 62.
- (en) William Crotch, « On the Derivation of the Scale, Tuning, Temperament, the Monochord, &c. », The Musical Times and Singing Class Circular, vol. 10, no 224, , p. 115-118 (DOI 10.2307/3355208, JSTOR 3355208, lire en ligne).
- (en) David Creese, The Monochord in Ancient Greek Harmonic Science, Cambridge, (ISBN 9780521843249), vii.
- Terpstra, Siemen (1993). " An Introduction to the Monochord ", Alexandria 2 : The Journal of the Western Cosmological Traditions, Volume 2, pp. 137-9. David Fideler, éd. Red Wheel/Weiser. (ISBN 9780933999978).
- Son utilisation courante est attestée par des illustrations telles que celle-ci, tirée d'un manuscrit normand du XIe siècle :
« Hybride tenant un monocorde et chantant », Université Paris-Sorbonne, Base de données Musiconis (consulté le ). - J. Murray Barbour, Tuning and Temperament: A Historical Survey [« Accordage et tempérament : une étude historique »], Dover/Courier, (ISBN 9780486317359), xlviii :
« Barbour utilise des guillemets autour de « ce que l'on pourrait appeler un « monopipe » ». »
Voir aussi
[modifier | modifier le code]Bibliographie
[modifier | modifier le code]- Claude Abromont et Eugène de Montalembert, Guide de la théorie de la musique, Librairie Arthème Fayard et Éditions Henry Lemoine, coll. « Les indispensables de la musique », , 608 p. [détail des éditions] (ISBN 978-2-213-60977-5)
- Cecil Adkins, « The Technique of the Monochord », dans Acta Musicologica, vol. 39 fasc.1/2, janvier – juin 1967, p. 34–43.

















