Multiplicité (mathématiques)

En mathématiques, on définit pour certaines propriétés la multiplicité d'une valeur ayant cette propriété. Il s'agit en général d'un nombre naturel qui indique « combien de fois » la valeur possède la propriété. Cela est dépourvu de sens en général (on possède une propriété ou on ne la possède pas), mais une interprétation naturelle existe dans certains cas. En général une propriété pour laquelle des multiplicités sont définies détermine un multiensemble de valeurs plutôt qu'un simple ensemble.

Multiplicité d'une racine d'un polynôme

Le cas le plus connu est la multiplicité d'une racine d'un polynôme non nul P. Un nombre r est racine de P si P(r) = 0, et dans ce cas on peut écrire P = (X − r)Q. Il peut arriver que r soit encore une racine de Q, et dans ce cas on peut écrire P = (X − r)^mR avec m ≥ 2, et le plus grand m pour lequel c'est possible est par définition l'ordre de multiplicité de r comme racine de P.

L'utilisation de l'ordre de multiplicité des racines est indispensable si on veut satisfaire les relations entre coefficients et racines.

Multiplicité d'une valeur propre

En algèbre linéaire, si ${\displaystyle \lambda }$ est la valeur propre d'un endomorphisme u d'un espace vectoriel E de dimension finie n, l'ordre de multiplicité géométrique de ${\displaystyle \lambda }$ est la dimension du sous-espace propre associé, et l'ordre de multiplicité algébrique est la dimension du sous-espace caractéristique associé. L'ordre de multiplicité algébrique est aussi égal à l'ordre de multiplicité ${\displaystyle m_{\lambda }}$ de la racine ${\displaystyle \lambda }$ dans le polynôme caractéristique de u.

S'il existe une base de l'espace vectoriel ${\displaystyle E}$ telle que la matrice associée à ${\displaystyle u}$ dans cette base, notée U, soit triangulaire (ce qui est toujours le cas si le corps K est algébriquement clos), alors le polynôme caractéristique de u est à la fois égal à ${\displaystyle \prod _{i=1}^{m}{(X-\lambda _{i})^{m_{\lambda _{i}}}}}$, où ${\displaystyle \lambda _{1},...,\lambda _{m}}$ sont les valeurs propres de u, et à ${\displaystyle \prod _{j=0}^{n}(X-U_{jj})}$. Par conséquent, ${\displaystyle n=\sum _{i=1}^{m}m_{\lambda _{i}}}$, et ${\displaystyle m_{\lambda }=\#\{j:(U)_{jj}=\lambda \}}$ (autrement dit, ${\displaystyle m_{\lambda }}$ est le nombre de fois que la valeur propre ${\displaystyle \lambda }$ apparaît dans la diagonale de la matrice ${\displaystyle U}$).

Multiplicité et anneau de valuation discrète

La notion de multiplicité intervient naturellement dans les anneaux de valuation discrète. Dans un tel anneau, il existe un élément irréductible t appelé uniformisante tel que pour tout élément a de l'anneau, il existe un élément b inversible et un entier n tel que ${\displaystyle a=bt^{n}}$, l'écriture étant unique. n s'appelle l'ordre de l'élément a et n'est autre que l'ordre de multiplicité de t dans la décomposition de a en éléments irréductibles.

Cette situation sert à définir l'ordre de multiplicité d'un pôle ou d'un zéro a d'une fraction rationnelle. On prend comme uniformisante l'élément X - a. Dans ce contexte, un élément inversible est une fraction rationnelle définie en a et qui ne s'annule pas en a. Si une fraction rationnelle f se décompose sous la forme ${\displaystyle f=(X-a)^{n}g}$, avec g inversible, a est un zéro de f de multiplicité n si n > 0, et a est un pôle de f de multiplicité -n si n < 0. On peut procéder d'une façon comparable pour définir l'ordre de multiplicité d'un zéro d'une fonction holomorphe, ou d'un zéro ou pôle d'une fonction méromorphe.

Point multiple d'une courbe algébrique

La cubique de Tschirnhaus, d'équation ${\displaystyle Y^{2}-3X^{2}+X^{3}=0}$, admet un point double à l'origine

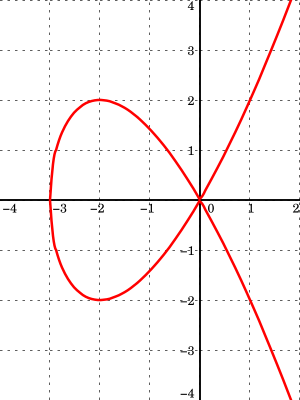
Considérons une courbe algébrique affine plane (V) d'équation ${\displaystyle F(X,Y)=0}$ et soit P un point de cette courbe. Par changement de variables, supposons que P soit égal au point (0,0). F s'écrit comme somme de polynômes homogènes ${\displaystyle F=\sum _{k=m}^{n}F_{m}}$ et le plus petit indice k tel que ${\displaystyle F_{k}}$ soit non nul s'appelle ordre de multiplité de F en P^[1],[2]. Si F est sans facteur multiple, ce qu'on supposera désormais, on l'appelle aussi multiplicité de la courbe en P. Si k = 1, on dit que P est un point simple de la courbe, si k = 2, on parle de point double, si k = 3 de point triple, etc. Si on factorise ${\displaystyle F_{m}}$ en facteurs du premier degré, chacun de ces facteurs définit une tangente à la courbe en P.

Dans l'exemple ci-contre, on a ${\displaystyle F_{2}=Y^{2}-3X^{2}}$ et ${\displaystyle F_{3}=X^{3}}$. L'ordre de multiplicité du point (0,0) est donc 2. La courbe admet deux tangentes en ce point d'équation ${\displaystyle Y=\pm {\sqrt {3}}X}$.

Si M(P) est l'idéal maximal des fonctions rationnelles s'annulant en P, dans l'anneau local ${\displaystyle O_{p}(V)}$ des fonctions rationnelles définies en P^[3], alors l'ordre de multiplicité m en P est le plus grand entier r tel que F appartiennent à ${\displaystyle M(P)^{r}}$. m est aussi égal à la dimension du quotient ${\displaystyle M(P)^{n}/M(P)^{n+1}}$ pour n assez grand (en fait dès que n est supérieur ou égal à m). Cette dernière propriété permet de définir la multiplicité en un point d'une courbe algébrique générale de façon intrinsèque. Dans l'exemple précédent, pour n = 2, une base de ${\displaystyle M(P)^{2}/M(P)^{3}}$ est donnée par ${\displaystyle \{X^{2},XY\}}$, compte tenu du fait que ${\displaystyle Y^{2}=3X^{2}{\rm {\;{mod}\;M(P)^{3}}}}$, et plus généralement, pour ${\displaystyle n\geq 2}$, une base de ${\displaystyle M^{n}/M^{n+1}}$ est donnée par ${\displaystyle \{X^{n},X^{n-1}Y\}}$. Donc m = 2.

La multiplicité de (V) en P est aussi égale à la multiplicité de l'intersection de la courbe (V) avec une droite passant par P mais qui n'est pas tangente à la courbe.

Multiplicité d'une intersection

Multiplicité d'intersection de deux courbes algébriques, le quadrifolium (en bleu) d'équation ${\displaystyle (x^{2}+y^{2})^{3}-4x^{2}y^{2}=0}$, et le trifolium (en rouge) d'équation ${\displaystyle (x^{2}+y^{2})^{2}+3x^{2}y-y^{3}=0}$. L'intersection en (0,0) est de multiplicité 14, à savoir 2 arcs du trifolium qui coupent transversalement 4 arcs du quadrifolium (soit 2 fois 4 points), et le dernier arc qui coupent transversalement 2 arcs du quadrifolium (soit 2 points) et qui est tangent aux deux autres (soit 2 points doubles).

Considérons deux courbes algébriques planes, sans composante commune, données par leurs équations respectives ${\displaystyle F(X,Y)=0}$ et ${\displaystyle G(X,Y)=0}$ et soit P un point. Soit ${\displaystyle O_{P}}$ l'anneau local des fractions rationnelles définies en P. On appelle multiplicité d'intersection des deux courbes en P, notée ${\displaystyle \mu _{P}(F,G)}$, la dimension du quotient ${\displaystyle O_{P}/(F,G)}$ en tant qu'espace vectoriel sur le corps de base. Celle-ci possède les propriétés suivantes^[4] :

• La multiplicité d'intersection en P est strictement positive si et seulement si P est un point commun aux deux courbes.
• Si P est un point simple des deux courbes et si les tangentes des deux courbes en P sont distinctes, cette multiplicité vaut 1.
• Si P est un point multiple de l'une des courbes ou des deux, et si les deux courbes n'ont pas de tangentes communes en P, alors ${\displaystyle \mu _{P}(F,G)}$ est égale au produit des multiplicités de F et G en P. S'il y a au moins une tangente commune, elle est strictement supérieure à ce produit.
• Si ${\displaystyle F=\prod _{i}F_{i}^{r_{i}}}$ et ${\displaystyle G=\prod _{j}G_{j}^{s_{j}}}$, alors ${\displaystyle \mu _{P}(F,G)=\sum _{i,j}r_{i}s_{j}\mu _{P}(F_{i},G_{j})}$.
• Pour tout polynôme A, ${\displaystyle \mu _{P}(F,G)=\mu _{P}(F,G+AF)}$, car résoudre les équations F = G = 0 est équivalent à résoudre les équations F = G + AF = 0.

L'utilisation de ces propriétés permet de calculer facilement la multiplicité de l'intersection des deux courbes en un point donné. On se ramène en général au point (0,0) après un changement de variables.

EXEMPLES :

• Soit ${\displaystyle F(X,Y)=Y+aX^{2}+bXY+cY^{2}+...}$ une courbe, dont la tangente en P = (0,0) est donnée par Y = 0. La multiplicité d'intersection de F et de sa tangente en P vaut :

${\displaystyle \mu _{P}(F,G)=\mu _{P}(Y+aX^{2}+bXY+cY^{2}+dX^{3}+...,Y)=\mu _{P}(aX^{2}+dX^{3}+...,Y)}$

${\displaystyle \;\;\;=\mu _{P}(X^{2},Y)+\mu _{P}(a+dX+...,Y)=2}$ si a est non nul et est strictement supérieur à 2 si a = 0 (cas d'un point d'inflexion par exemple).

• Soit la parabole annulant ${\displaystyle F(X,Y)=Y-X^{2}-X}$, le cercle annulant ${\displaystyle G(X,Y)=X^{2}+Y^{2}-2aX-2bY+c}$, et P = (0,0). On pourra vérifier, en appliquant les propriétés énoncées que :

si c est non nul, ${\displaystyle \mu _{P}(F,G)=0}$. Le cercle ne passe pas par P.

si c =0 et a + b non nul, ${\displaystyle \mu _{P}(F,G)=1}$. Le cercle est sécant à la parabole en P.

si c = a + b = 0 et b différent de 1, ${\displaystyle \mu _{P}(F,G)=2}$. Le cercle est tangent en P à la parabole.

si c = 0, a = -1, b = 1, ${\displaystyle \mu _{P}(F,G)=3}$. Le cercle est osculateur en P à la parabole.

• Soit la parabole annulant ${\displaystyle F(X,Y)=Y-X^{2}}$, le cercle annulant ${\displaystyle G(X,Y)=X^{2}+Y^{2}-Y}$, et P = (0,0). Alors ${\displaystyle \mu _{P}(F,G)=4}$. Le cercle est surosculateur à la parabole en P.

L'utilisation de la multiplicité d'une intersection est indispensable dans l'application du théorème de Bézout.

Références

1. Daniel Perrin, Géométrie algébrique, EDP (1995), p.113
2. William Fulton, Algebraic curves, W. A. Benjamin (1974), p.66
3. Dans le cas d'une courbe plane, M(P) est engendré par X et Y si P = (0,0)
4. William Fulton, Algebraic curves, W. A. Benjamin (1974), p.74

• Portail des mathématiques