Oscillateur de Van der Pol

L’oscillateur de Van der Pol est un système dynamique à temps continu à deux degré de liberté. Il est décrit par une coordonnée x(t) vérifiant une équation différentielle faisant intervenir deux paramètres : une pulsation propre ω₀ et un coefficient de non-linéarité ε. Lorsque ε = 0, cet oscillateur se réduit à un oscillateur harmonique pur.

Il porte le nom de Balthasar van der Pol.

Histoire

Ce circuit électronique à base de triode développe un régime d'oscillations forcées régies par l'équation de Van der Pol^[1] (les composants passifs sont : une résistance R, un condensateur C et un circuit couplé d'inductance L et de inductance mutuelle M) . Le circuit RLC monté en série est parcouru d'un courant i, et l'anode (ou plaque) de la triode reçoit un courant i_a, tandis que la tension aux bornes de la grille de la triode est notée u_g. L’oscillateur de Van der Pol est mis en régime forcé par une source de tension alternative E_s.

L’oscillateur de Van der Pol a été imaginé par le physicien néerlandais Balthasar van der Pol alors qu'il était employé par les laboratoires Philips^[2]. Van der Pol découvrit que ce circuit contenant un tube à vide développait des oscillations stables, qu'il appela « oscillation de relaxation^[3] » et que l'on désigne aujourd'hui plutôt comme des cycles limites des circuits électriques. Lorsque ces circuits sont excités à une fréquence proche de celle du cycle limite il se crée un couplage, c'est-à-dire que le signal de commande impose sa fréquence au courant. Van der Pol et son collègue Van der Mark publièrent en 1927^[4] qu'à certaines fréquences de commande, il apparaissait un bruit irrégulier. Ce bruit se déclenchait toujours au voisinage des fréquences naturelles de couplage. Ce fut l'une des premières mises en évidence de l'existence d'un chaos déterministe^[5],[6].

L’équation de Van der Pol a trouvé de nombreuses applications dans les sciences physiques et biologiques. Par exemple, en biologie, Fitzhugh^[7] et Nagumo^[8] ont développé une version bidimensionnelle de ce système dynamique pour décrire le potentiel d'action des neurones. L’équation a aussi été utilisée en sismologie pour modéliser l’interaction des plaques sur une faille^[9].

Oscillateur libre

L'équation différentielle de l'oscillateur libre s'écrit :

${\displaystyle {\frac {\mathrm {d} ^{2}x(t)}{\mathrm {d} t^{2}}}-\varepsilon \omega _{0}\left(1-x^{2}(t)\right){\frac {\mathrm {d} x(t)}{\mathrm {d} t}}+\omega _{0}^{2}x(t)=0.}$

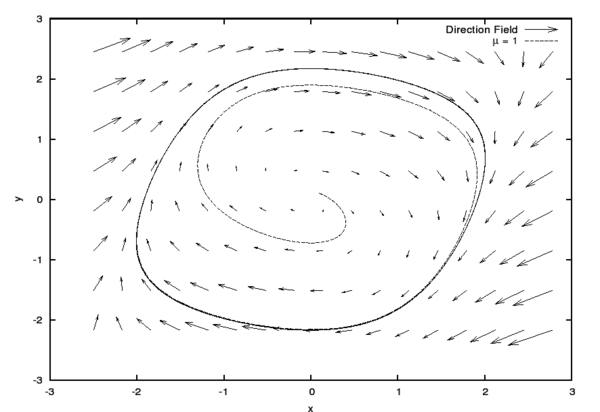
Lorsque ε ≠ 0, ce système dissipatif possède une dynamique régulière caractérisée par un attracteur en forme de cycle limite, représenté sur la figure ci-dessous (où on a posé ω₀ = 1) :

Oscillateur forcé

Comportement chaotique de l'oscillateur avec forçage sinusoïdal.

Lorsque cet oscillateur est excité par un terme harmonique à la pulsation ω, son équation différentielle devient :

${\displaystyle {\frac {\mathrm {d} ^{2}x(t)}{\mathrm {d} t^{2}}}-\varepsilon \,\omega _{0}\left(1-x^{2}(t)\right){\frac {\mathrm {d} x(t)}{\mathrm {d} t}}+\omega _{0}^{2}\ x(t)=\omega _{0}^{2}\,X\cos(\omega t)}$

Notes

1. (en) K. Tomita, « Periodically forced nonlinear oscillators », Chaos, Arun V. Holden, Manchester University Press,‎ 1986, p. 213–214 (ISBN 0719018110).
2. M.L. Cartwright, « Balthazar van der Pol », J. London Math. Soc., n^o 35,‎ 1960, p. 367-376 (lire en ligne).
3. B. Van der Pol, « On relaxation-oscillations », The London, Edinburgh and Dublin Phil. Mag. & J. of Sci., 2^e série, n^o 7,‎ 1927, p. 978-992.
4. B. Van der Pol et J. Van der Mark, « Frequency demultiplication », Nature, n^o 120,‎ 1927, p. 363-364.
5. T. Kanamaru, « Van der Pol oscillator », Scholarpedia, 2^e série, n^o 1,‎ 2007, p. 2202 (lire en ligne).
6. Jean-Marc Ginoux, « Van der Pol and the history of relaxation oscillations: Toward the emergence of a concepts », Chaos, n^o 22,‎ 2012 (DOI 10.1063/1.3670008)
7. R. FitzHugh,, « Impulses and physiological states in theoretical models of nerve membranes », Biophysics J., n^o 1,‎ 1961, p. 445-466.
8. J. Nagumo, S. Arimoto et S. Yoshizawa, « An active pulse transmission line simulating nerve axon », Proc. IRE, n^o 50,‎ 1962, p. 2061-2070.
9. J. Cartwright, V. Eguiluz, E. Hernandez-Garcia et O. Piro, « Dynamics of elastic excitable media », International Journal of Bifurcation and Chaos Appl. Sci. Engrg., n^o 9,‎ 1999, p. 2197–2202.

Voir aussi

Articles connexes

• Travaux d'André Blondel sur les oscillations auto-entretenues linéaires et non-linéaires
• Système dynamique
• Théorie du chaos

Liens externes

• Une animation Flash interactive (présentation).
• Une applet

Bibliographie

• Jean-Marc Ginoux, Histoire de la théorie des oscillations non linéaires : De Poincaré à Andronov, Hermann, 2015.
• James Gleick (trad. Christian Jeanmougin), La Théorie du Chaos [« Chaos: Making a New Science »], Paris, Flammarion, coll. « Champs », 1988 (réimpr. 1999, 2008), 431 p. (ISBN 978-2-08-081219-3 et 2-08081-219-X), p. 41-43
  contient une description détaillée de l’oscillateur à tube de van der Pol. Après avoir publié un article sur ce même sujet en 1988 dans le New York Times, Gleick avait reçu d'un lecteur du journal un circuit électronique analogue au circuit de Van der Pol. L'article en question : (en) David Colman, « There's No Quiet Without Noise », New York Times,‎ 11 juillet 2011 (lire en ligne, consulté le 11 juillet 2011)
• Hervé Reinhard, Équations différentielles : Fondements et applications, Paris, Gauthier-Villars, coll. « µB », 1988, 450 p. (ISBN 2-04-015431-0), « 8 - Equations et solutions périodiques »
• (en) Balthazar van der Pol et J van der Mark, « The Heartbeat considered as a Relaxation oscillation, and an Electrical Model of the Heart », Philosophical Magazine Supplement, n^o 6,‎ 1928, p. 763-775.
• (en) Shawnee L. Mc Murran et James J. Tattersall, « Cartwright and Littlewood on van der Pol's equation, Harmonic analysis and nonlinear differential equations », Contemporary Mathematics, Riverside, CA, American Mathematical Society (Providence, RI, 1997), n^o 208,‎ 1995, p. 265-276.

• Portail de l'analyse
• Portail de la physique