Pentation

Les trois premières valeurs de l'expression x[5]2. La valeur de 3[5]2 est d'environ 7,626 × 1012 ; les valeurs pour les x plus élevés, comme 4[5]2, qui est d'environ 2,361 × 108,072 × 10153, sont beaucoup trop grandes pour apparaître sur le graphique.

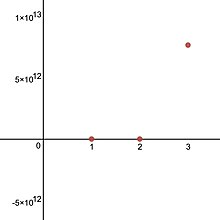
La pentation est la répétition de l'opération de tétration, comme la tétration est la répétition de l'opération d'exponentiation. La pentation est une hyperopération.

Comme la tétration, la pentation a peu d'applications dans la vie courante. Elle est non commutative, et a donc deux fonctions inverses, qui pourraient être appelées la penta-racine et le penta-logarithme (analogues aux deux fonctions inverses pour l'élévation à une puissance : racine et logarithme). La pentation borne également les fonctions récursives élémentaires.

Le mot pentation a été inventé par Reuben Goodstein à partir de penta- (cinq) et itération. Cela fait partie de sa convention de notation générale pour les hyperopérations.

La pentation peut s'écrire dans la notation des puissances itérées de Knuth comme ${\displaystyle a\uparrow \uparrow \uparrow b}$ ou ${\displaystyle a\uparrow ^{3}b}$.

Prolongement

On ne sait pas comment prolonger la pentation aux nombres complexes ou aux réels non entiers.

Prolongement aux nombres négatifs ou nuls

Par l'utilisation du super-logarithme, ${\displaystyle a\uparrow ^{3}b}$ peut être défini quand b est négatif ou nul pour un nombre limité de valeurs de b. Ainsi, pour toutes les valeurs entières strictement positives de a, la pentation négative est définie comme suit :

• ${\displaystyle a\uparrow ^{3}0=\operatorname {slog} _{a}a=1}$ si a > 1.
• ${\displaystyle a\uparrow ^{3}-1=\operatorname {slog} _{a}1=0}$ si a > 1.
• ${\displaystyle a\uparrow ^{3}-2=\operatorname {slog} _{a}0=-1}$ si a > 1.

Pour ce qui des valeurs négatives de a, seul a = -1 peut donner lieu à une extension. Dans ce cas, selon les valeurs du nombre entier positif b, les trois valeurs possibles que l'on obtient pour ${\displaystyle -1\uparrow ^{3}b}$ sont indiquées ci-dessous :

• ${\displaystyle -1\uparrow ^{3}b={^{1}{-1}}=-1}$ si b est congru à 1 modulo 3.
• ${\displaystyle -1\uparrow ^{3}b={^{-1}{-1}}=0}$ si b est congru à 2 modulo 3.
• ${\displaystyle -1\uparrow ^{3}b={^{0}{-1}}=1}$ si b est congru à 0 modulo 3.

Valeurs particulières

Comme l'opération à partir de laquelle elle est définie (la tétration) est difficile à prolonger à des hauteurs non entières, la pentation ${\displaystyle a\uparrow ^{3}b}$ est dans l'état actuel des connaissances définie uniquement pour des valeurs entières de a > 0 et de b ≥ 0, et à titre exceptionnel pour certains entiers négatifs. Comme toutes les autres hyperopérations d'ordre 3 (élévation à une puissance) et plus, la pentation a les cas triviaux suivants (identités) valables pour toutes les valeurs de a et b du domaine :

• ${\displaystyle 1\uparrow ^{3}b=1}$
• ${\displaystyle a\uparrow ^{3}1=a}$

En dehors des cas triviaux indiqués ci-dessus, la pentation produit des nombres extrêmement grands très rapidement, de sorte qu'un très petit nombre de cas non triviaux produisent des valeurs pouvant être écrites dans la notation conventionnelle, comme illustré ci-dessous :

• ${\displaystyle 2\uparrow ^{3}2={^{2}2}=4}$
• ${\displaystyle 2\uparrow ^{3}3={^{^{2}2}2}=^{4}2=65536}$
• ${\displaystyle 2\uparrow ^{3}4={^{^{^{2}2}2}2}=^{65536}2=2^{2^{2^{\cdot ^{\cdot ^{\cdot ^{2}}}}}}{\mbox{ (une tour de puissance de taille 65 536) }}\approx \exp _{10}^{65533}(4,29508)}$ (montré ici dans la notation exponentielle itérée car ce nombre est bien trop grand pour être écrit dans la notation conventionnelle. ${\displaystyle \exp _{10}(n)=10^{n}}$.)
• ${\displaystyle 3\uparrow ^{3}2={^{3}3}=7625597484987}$
• ${\displaystyle 3\uparrow ^{3}3={^{^{3}3}3}={^{7625597484987}3}=3^{3^{3^{\cdot ^{\cdot ^{\cdot ^{3}}}}}}{\mbox{ (une tour de puissance de taille 7625597484987) }}\approx \exp _{10}^{7625597484986}(1,09902)}$
• ${\displaystyle 4\uparrow ^{3}2={^{4}4}=4^{4^{4^{4}}}=4^{4^{256}}\approx \exp _{10}^{3}(2{,}19)}$ (un nombre avec plus de 10¹⁵³ chiffres)
• ${\displaystyle 5\uparrow ^{3}2={^{5}5}=5^{5^{5^{5^{5}}}}=5^{5^{5^{3125}}}\approx \exp _{10}^{4}(3{,}33928)}$ (un nombre avec plus de 10¹⁰²¹⁸⁴ chiffres)

Voir aussi

Articles connexes

• Hyperopération
• Notation des puissances itérées de Knuth
• Notation des flèches chaînées de Conway

Bibliographie

• Sur les hyperopérations

  Reuben Louis Goodstein, « Transfinite ordinals in recursive number theory », Journal of Symbolic Logic, vol. 12, n^o 4, 1947, p. 123-129

• Sur la notation fléchée de Knuth

  Donald Ervin Knuth, « Mathematics and Computer Science: Coping with Finiteness », Science, vol. 194, n^o 4271, 1976, p. 1235-1242

Lien externe

(en) Tetration Forum par Jay D. Fox

Crédit d'auteurs

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Pentation » (voir la liste des auteurs).

• Arithmétique et théorie des nombres