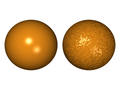Placage de relief

Le placage de relief[1], ou topographie d’aspérité[2] également nommé sous son appellation anglaise de bump mapping, est un terme informatique qui désigne la technique utilisée en infographie et qui sert à donner du relief aux modèles 2D ou 3D, ou aux textures. Elle fut initialement utilisée en ray-tracing[réf. nécessaire], où la technique consiste à modifier la normale de la surface.

Les termes placage de rugosité[1] et texture par perturbation de la lumière sont également utilisés[réf. nécessaire].

Explications

[modifier | modifier le code]

Le placage de relief est une technique permettant d'ajouter du relief à une surface grâce à l'interaction entre la lumière de l'environnement et une texture irrégulière appliquée sur cette surface. Pour faire une analogie avec la vie réelle, sachez que le relief des objets provient de la lumière reflétée par cet objet à sa surface. L'œil perçoit donc les variations de lumière, les interprète suivant l'angle de réflexion et en déduit le relief. Le placage de relief utilise donc une astuce pour générer des effets d'éclairages qui vont simuler la lumière naturelle pour nous donner la même impression que dans la réalité, et nous percevrons donc mieux le relief des textures en 3D. C'est donc principalement tout un travail sur les jeux d'ombres et de lumières qui donne au placage de relief toute son utilité. DirectX et OpenGL sont deux des interfaces de programmation qui permettent de décoder et d'utiliser le placage de relief. Initialement exclusif aux cartes graphiques Matrox G400 séries sorties en 1999, le bump mapping est supporté depuis 2004 par les cartes graphiques ATI et nVidia.

Images

[modifier | modifier le code]

En virtuel

[modifier | modifier le code]
Sphère sans placage de relief ; Relief qui sera appliqué à la sphère ; Sphère avec placage de relief

L’image ci-contre est un exemple d'application du placage de relief sur une sphère. Sur la première image à gauche la sphère semble lisse. Tandis que sur l'image de droite, le placage de relief est bien présent. L'image au centre est la texture qui indique le niveau de relief qui sera appliqué.

Galerie

[modifier | modifier le code]

Notes et références

[modifier | modifier le code]
  1. ↑ a et b (en) Neal Roger Tringham, Dictionnaire des techniques et technologies nouvelles - Anglais/français (4e ed.), Lavoisier, , 582 p. (ISBN 9782743019693), p. 70.
  2. ↑ Blender 2.6 : 3D pour l’architecture, p. 178, Matthieu Dupont de Dinechin

Voir aussi

[modifier | modifier le code]

Articles connexes

[modifier | modifier le code]

Liens externes

[modifier | modifier le code]